基于励磁感抗的励磁涌流鉴别方法分析

冉亮亮，刘国平,，徐 岩，张兰钦，李天阳

(1.华北电力大学，河北 保定 071003；2.石家庄供电公司，石家庄 050051)

在变压器差动保护中使用的励磁涌流判别方法，如二次谐波原理、间断角原理、波形对称原理，都是采用励磁涌流波形的某一个特征量来区分涌流和故障电流[1-5]，不能全面的反映励磁涌流的特征[6-7]。而同时利用电压量和电流量的变压器保护新原理中的磁通特性原理[8-15]，从励磁支路的非线性特性出发，应用前景广泛，然而目前其仅适用于单相变压器组。在基于电子式互感器的智能化变电站中，对于变压器保护而言，电子式互感器良好的暂态特性以及相对较高的采样速率，为基于磁通的一些新的涌流算法研究提供了良好的条件。基于励磁感抗的励磁涌流鉴别方法,在电子式互感器发展的有利背景下，从励磁涌流的产生原因出发，由励磁感抗反映了磁化曲线的变化，从而反映了励磁涌流时变压器铁心的磁化情况。以下对基于励磁感抗的励磁涌流鉴别方法进行分析。

1 单相变压器磁通制动原理

变压器等值电路如图1所示。

图1 变压器等值电路示意

其中，R1、L1分别为原边绕组电阻电感，设变压器绕组端电压为U1，只考虑变压器原边，流进绕组的电流i1与该变压器互感磁链、漏感磁链之间的关系为：

(1)

(2)

设L为漏感，则由于漏感L一般很小，可近似认为为0，同时忽略绕组电阻和电感，则有：

(3)

在互感磁链当中i1和i2进行抵消，其差流部分看作是励磁涌流id，设M为变压器的励磁感抗，则：

(4)

或者记磁化曲线的斜率为k，对(3)式进行如下变形：

(5)

从励磁电感和电流电压的关系可以看出，励磁电感的变化反映磁化曲线的变化，和磁化曲线斜率k是等同的。而电压和电流的微分是很容易求得的，所以式(4)最终变为：

(6)

从励磁涌流的产生原因出发可知，M值很本质的反映出磁化曲线的状态，所以根据M值的变化可以确定变压器的运行状态。图2、图3分别示意了涌流和故障情况下差流和M值的变化规律。

图2 励磁涌流与励磁电感的关系

图3 故障电流与励磁电感的关系

对于微机保护，电压和电流瞬时值的测量和计算很方便，将式(6)进行简化为：

(7)

不同于传统的利用整周期数据的磁通特性方法，将电压波形分成上升沿和下降沿不同的区段，以上升沿为例计算M值(下降沿时计算方法与上升沿的一样)，如保护装置为每周波48点采样，1/4周波可计算12次M值，如果有连续三次满足

Mn-Mn+6≥k

(8)

判为励磁涌流，否则判为故障电流。可见整个计算过程只需1/4周波的时间，并且只用差流的上升沿或下降沿计算，计算量小。

该算法是对变压器励磁涌流最全面、最本质的反映，简单可靠。可准确的判断励磁涌流和故障电流，可以在1/4基波的时间内出口(继电器动作除外)，突破了传统变压器保护动作需要一个完整基波的时间瓶颈。

2 三相变压器励磁涌流鉴别方法

在单相变压器磁通制动原理的基础上，对常见三相变压器绕组为三角形接线时的基于励磁感抗的励磁涌流鉴别方法进行分析。

当三相变压器的电源侧为三角接法时，无法测到绕组中的电流[16]。图4为Y/Δ接线的三相变压器模型。

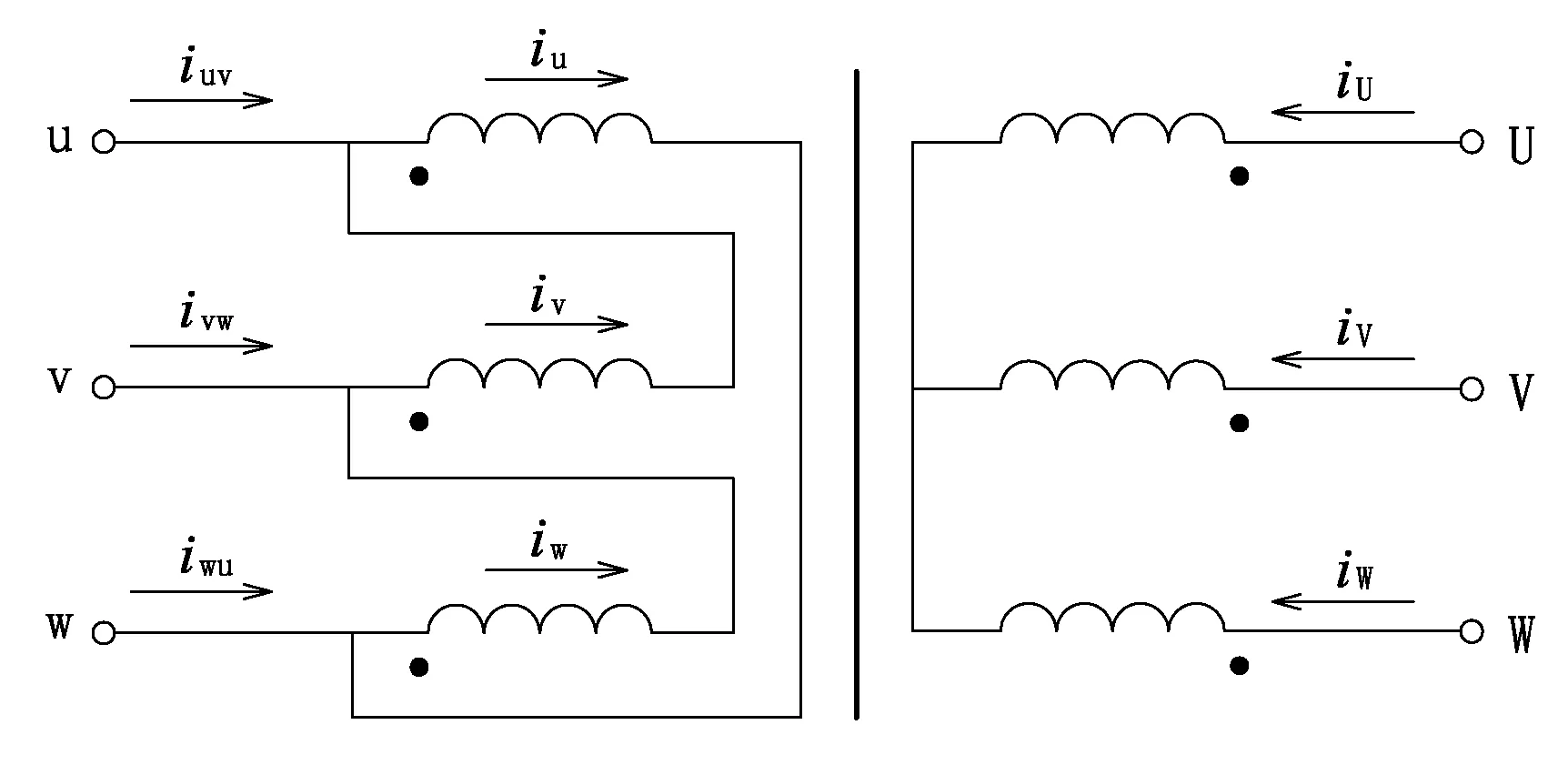
图4 Y/Δ接线的三相变压器模型

对变压器三角侧有下式成立：

(9)

式中：uuw、uvu、uwv和iu、iv、iw分别为变压器绕组u、v、w相的瞬时相电压、瞬时相电流；L为变压器绕组的漏感(设三相绕组漏抗相等)；ψu、ψv、ψw分别为变压器u、v、w相绕组的相磁链。将式(9)等号两端两两相减，得下式

(10)

由变压器的工作原理，式(10)可进行如下变换：

(11)

式中：uuv、uvw、uwu和iuv、ivw、iwu分别为变压器各相绕组的线电压、线电流；ψuv、ψvw、ψwu为变压器各相绕组磁链之间的差。忽略L，式(11)可变换为

(12)

如图4所示，uuv、uvw、uwu、uuw、uvu、uwv、iuv、ivw、iwu可由变压器端部的电压互感器和电流互感器测量出来。

因此当电源侧为三角形接法时，经过分析推导，仍可得到类似于单相变压器励磁感抗与电压电流的关系，所以，三相变压器中，由Muv、Mvw、Mwu的大小变化趋势也可以对变压器是否发生故障做出快速判断，所以基于励磁感抗的励磁涌流鉴别方法对此种情况仍然适用。

3 动态模拟试验

为验证基于励磁感抗的励磁涌流鉴别方法的可行性，对变压器进行了各种运行工况的动模试验，并将各种状态下变压器的电压、电流进行了录波。利用这些实测的数据对算法的可行性进行了验证。

动模试验中，试验变压器是由3台单相DGM-10型模拟变压器组成的三相变压器，系统的接线图如图5所示。

图5 动模试验系统接线示意

本次试验模拟了变压器的各种运行状态，包括正常运行、空载合闸、空投于内部接地故障、空投于内部匝间故障、空投于内部相间故障。为了充分考虑不同时刻以及不同相别的影响，每种故障类型都考虑了不同相别，并进行多次试验。

对各种状态下的录波数据进行分析后发现，变压器负载运行下的故障状态，其励磁感抗都偏小；当变压器内部发生严重故障时，电流剧增，电压下降，励磁感抗迅速减小，k值也很小，且变化不大；当变压器出现励磁涌流时，励磁感抗很大，k值也随之变化。在绘制波形时，一个周期取40个点，变压器故障状态时M值和励磁涌流时M值的波形如图6所示可见，符合不同运行状态下对励磁感抗的分析。

另外，在求励磁感抗M值时，由于电压不一定和电流差值同时过零点，所以在电流差值过零点附近的M值可能就会发生跳跃，其值非常大，但其点数并不是很多，并不影响对励磁涌流的判断。

现以一个周期采样48点为例，对各次动模试验的数据进行如图7所示的程序流程的计算，求取k。

(a) 变压器单相短路 (b) 变压器两相接地短路

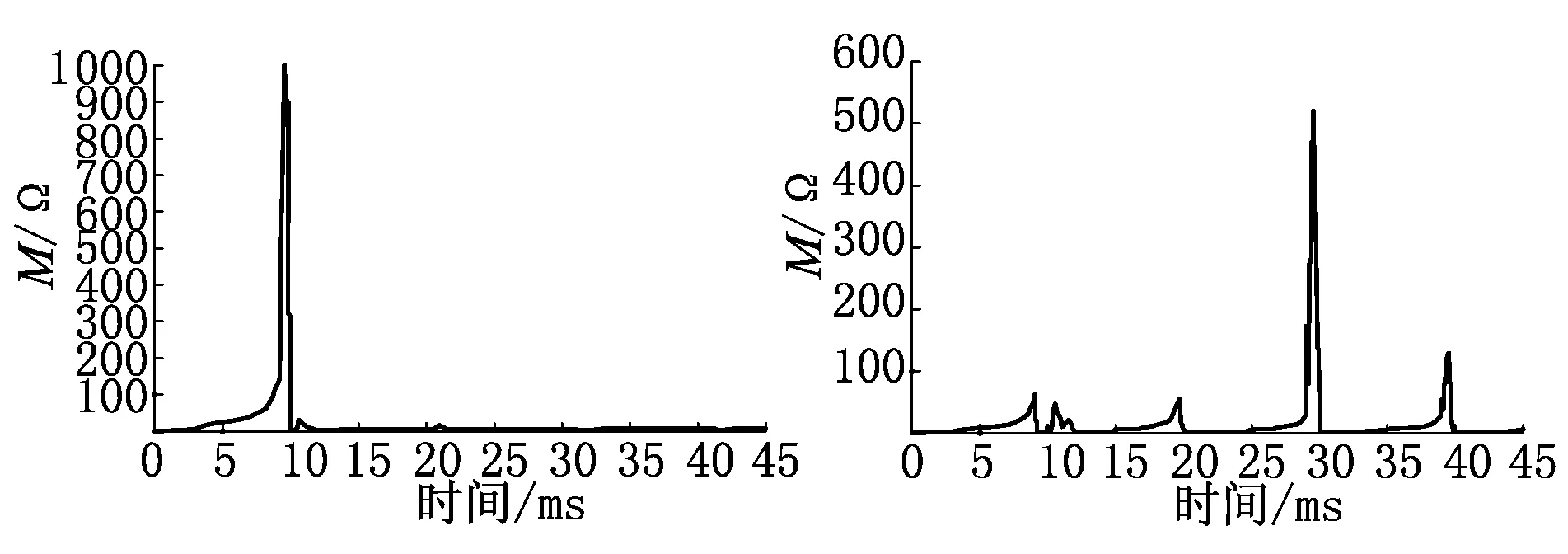
(c) 变压器三相短路 (d) 变压器匝间短路

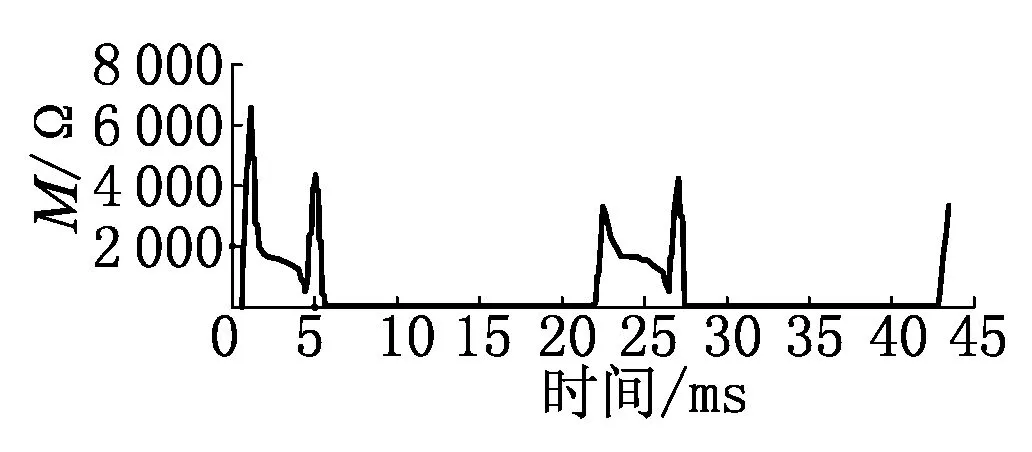
(e) 变压器励磁涌流时

图7 动模数据处理程序流程

通过以上流程处理每一次动模实验数据，对求得的k值进行分析比较，根据不同故障时k值的大小规律不同，逐渐调整修正k值，最后得出k值近似取1/4的差动电流即可满足要求。

4 现场应用情况

4.1 变压器励磁涌流故障

将基于励磁感抗的励磁涌流鉴别方法应用于现场变压器，可以在涌流发生时快速可靠的进行识别，进行闭锁，进一步证实了其可行性。某220 kV变电站3号主变压器空投而出现的励磁涌流录波见图8。

图8 励磁涌流录波

用基于励磁感抗的励磁涌流鉴别方法的分析过程，采样率为10 kHz，每周期采样200点，按公式(7)及下式：

Mn-Mn+25≥k

(13)

计算此状态下1/4周期内的k值，结果如图9所示。可知，远远大于差动保护电流定值(0.77 A)的1/4，即说明k值取1/4差动保护电流定值的基于励磁感抗的励磁涌流鉴别方法可以对变压器励磁涌流进行快速识别。

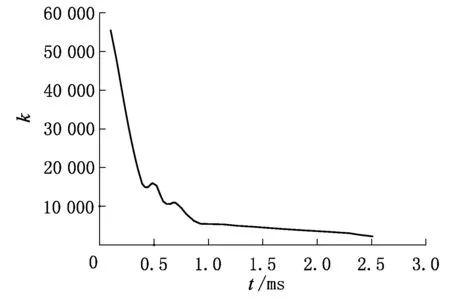
图9 变压器励磁涌流k值分布示意

4.2 变压器内部故障

某地区某变电站，某110 kV线路重合于三相故障，尚未切除时，1号主变压器于20:10:50时刻发生内部故障。图10为故障录波图。220 kV母线电压降到故障前的94.6%，通过计算各瞬时值下励磁感抗得知，k值远小于各相差动电流的1/4。同样，每周期采样200点，以1号主变压器U相为例，1WJ RCS978保护差动电流为0.46倍额定电流，U相差动电流的1/4经计算为54.28 A。计算此状态下1/4周期内的k值，结果如图11所示。

可见，k值分布都远小于54.28 A，从而验证了基于励磁感抗的励磁涌流鉴别方法可以对变压器内部故障做出快速判断并出口继电器。

5 结束语

在对鉴别励磁涌流原理的分析研究基础上，基于磁通制动原理，提出了三相变压器也适用的基于励磁感抗的励磁涌流鉴别方法。同时，通过大量动态模拟试验，对变压器进行了各种运行工况的动模试验，并通过现场变压器的励磁涌流以及故障的录波数据对其进行了验证，证实了基于励磁感抗的励磁涌流鉴别方法的可行性。

图10 变压器故障录波

图11 变压器故障k值分布

参考文献：

[1] 邵德军，尹项根，张 哲，等．改进型二次谐波励磁涌流制动方法[J]．电网技术，2006，30(24)：84-88.

[2] 朱亚明，郑玉平，叶 锋，等．间断角原理的变压器差动保护的性能特点及微机实现[J]．电力系统自动化，1996，20(11)：36-40.

[3] 孙志杰，陈云仑．波形对称原理的变压器差动保护[J]．电力系统自动化，1996，20(4)：42-46.

[4] 苗友忠，贺家李，孙雅明．变压器波形对称原理差动保护不对称度K的分析和整定[J]．电力系统自动化，2001，25(16)：26-29，44.

[5] 林湘宁，刘世明，杨春明，等．几种波形对称法变压器差动保护原理的比较研究[J]．电工技术学报，2001，16(4)：44-49，70.

[6] 王增平，马 静．关于变压器主保护的若干问题[J]．电力系统保护与控制，2008，36(14)：4-12.

[7] 王立大，段周朝．变压器励磁涌流引起保护误动分析[J]．电力系统保护与控制，2010，38(10)：138-140，144.

[8] 唐跃中，刘 勇，郭 勇，等．几种变压器励磁涌流判别方法的特点及其内在联系的分折[J]．电力系统自动化，1995，19 (9)：53-59.

[9] 王国兴，张传利，黄益庄．变压器励磁涌流判别方法的现状及发展[J]．中国电力，1998，31(10)：19-22.

[10] 宗洪良，金华峰，朱振飞，等．基于励磁阻抗变化的变压器励磁涌流判别方法[J]．中国电机工程学报，2001，21(7)：91-94．

[11] 毕大强，王祥珩，王 剑，等．基于非饱和区等效瞬时电感的变压器励磁涌流鉴别方法[J]．电力自动化设备，2005，25(10)：1-6.

[12] 葛宝明，于学海，王祥珩，等．基于等效瞬时电感判别变压器励磁涌流的新算法[J]．电力系统自动化，2004，28(7)：44-48.

[13] 葛宝明，苏鹏声，王祥珩，等．基于瞬时励磁电感频率特性判别变压器励磁涌流[J]．电力系统自动化，2002，26(17)：35-40.

[14] 闫晨光，郝治国，张保会，等．基于电压、电流信息的变压器保护原理分析[J]．电力自动化设备，2010，30(10)：37-41.

[15] 孙志杰，曾献华，汤汉松，等．磁通制动原理在变压器差动保护中应用[J]．电力自动化设备，2005，25(1)：79-81.

[16] 徐 岩．电力变压器内部故障数字仿真及其保护新原理的研究[D]．保定：华北电力大学，2005.