埋深对矿山压力影响的常微分方程解法研究

郭海英，王长建

(1.山西阳泉固庄煤矿，山西 阳泉 045060;2.河南理工大学能源学院，河南 焦作 454000)

在大多情况下，矿山压力显现会对采矿工程造成不同程度的危害。为了使矿山压力显现对正常的采矿工作不产生影响，必须采取各种措施把矿山压力显现控制在一定范围内。以避免造成巨大的人员伤亡和财产损失。因此，事先对各个煤层处的矿山压力进行估测显得越来越重要。

矿山压力现场观测研究法是在生产现场对矿山压力大小进行观测和记录，利用各种仪表、工具观测采场围岩变形、位移、顶底板破坏、支架受载荷及压缩等情况，然后从动态分析中得出对采场矿山压力显现有显著影响的岩层运动的条件、时间和方向以及采场周围支承压力的变化状况，为解决现场矿山压力控制问题提供依据。由于现场观测获得的资料反映多种因素的相互作用，用已经测得浅部矿山压力数据预测深处矿山压力的大小，具有可靠方便的特点。故利用这种资料预测分析深部矿山压力大小较为可靠，效果显著，越来越为生产现场认可采用。

为此，本文运用常微分方程的数值解为方法，根据实验数据，研究得出煤炭埋深与其所受矿山压力大小的变化规律，进而对煤炭埋深处的矿山压力值进行预测，为煤炭开采时开挖巷道所需支护强度进行预测并提供理论依据。

1 问题分析

某煤矿煤炭赋存深度平均约为500 m，现在需要初步预测煤层处所受的矿山压力大小。根据煤层上方0～50 m测量得到一组数据，见表1，根据测得的数据得到此处矿山压力大小，大体可用微分方程x2+x－y来表示，其中y是井下某煤层处的矿山压力，x是对应的煤层埋深，且假定地表平面的压力为零。

2 常微分方程的数值解法

常微分方程(组)的解是一个函数或一族函数。所谓数值解法就是寻求解函数自变量的一系列离散点上的近似值。常微分方程的数值解法很多，常用的是欧拉公式。考虑微分方程的初值问题:

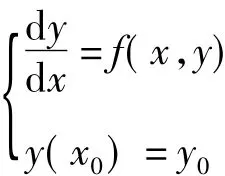
把微分方程中的导数用折线的斜率代替，得到:

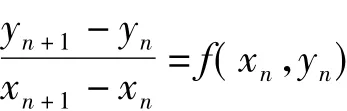
假设对于不同的n有xn+1－xn相同，记为h=xn+1－xn得到yn+1=yn+hf(xn，yn)基本的欧拉公式，其中，h称为步长。

3 算法的Matlab实现

3.1 实验数据

在本实验中，矿山工作人员已测得u在50 m内的矿山压力大小，见表1。

表1 50 m内矿山压力大小测量值

3.2 Matlab程序代码

常微分方程数值解法Matlab程序:

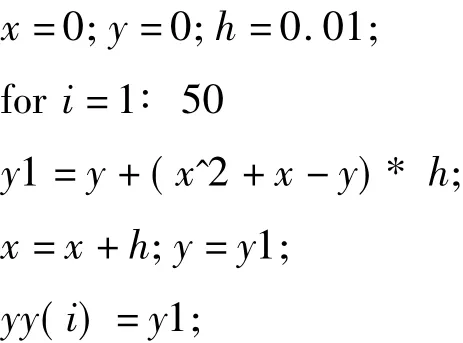
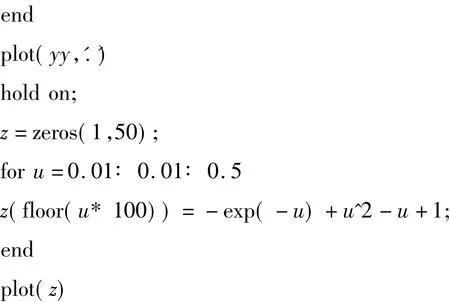
4 计算结果及分析

4.1 计算结果

为了便于对实验数据和数值解进行比较，在此把实验中得到的两种数据放在一起，具体数据见表2。

表2 不同u值得到的两种解析值和数值

4.2 Matlab图形

欧拉公式计算的数值解与解析解示意图见图1。

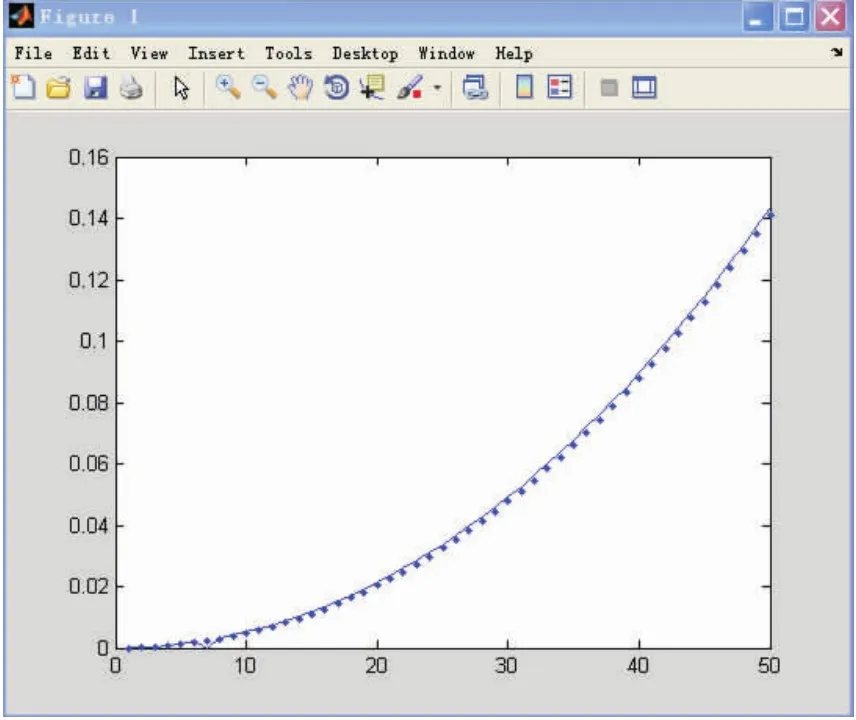
图1 欧拉公式计算的数值解与解析解示意图

4.3 结果分析

从表2和图1可知，用数值法得到的数据与用解析方法得到的数据基本是一致的，当u=5时，误差为3，当u=50时，误差为25。随着u的增大，数值解与解析解的误差也逐渐增大，但是变化量比较小。从图1可以看出，随着埋深的增大，矿山压力的值越来越大，而且，开始时矿山压力增加比较缓慢，深度越大矿山压力增长越快。由此得出的矿山压力变化情况，进而得出不同埋深处所受矿上压力的大体范围。在此可以预测u为500 m时，矿山压力值为21 MPa。

5 结论

本文运用常微分方程数值解法，分析了埋深变化对矿山压力的影响，根据预测方程得出了不同埋深与其所受矿山压力大小的关系，结果表明:

1)不同埋深的煤层所受的矿山压力大小不同，埋深越深，所受到的矿山压力越大。

2)在一定范围内，可以根据较浅深度的矿山压力值预测较深处的矿山压力大小，预测结果与真实值比较接近。

［1］钱鸣高，石平五，许家林.矿山压力与岩层控制［M］.徐州:中国矿业大学出版社，2010:353－371.

［2］王高雄，周之铭.常微分方程［M］.北京:高等教育出版社，2006:19－21.

［3］孙 祥，徐流美，吴 清.matlab7.0基础教程［M］.北京:清华大学出版社，2005:382－385.

［4］王 辉.大埋深采煤工作面矿压特征的数值模拟［J］.煤炭科学技术，2010(6):73－75.