基于“价值-成本”策略的空集装箱调运模型
刘爽阳,廖丽平
(西南交通大学 交通运输与物流学院,硕士研究生,四川 成都 610031)
随着我国经济的发展和铁路基础设施建设的加快,安全、迅速、方便、节约的集装箱运输进入了高速发展的阶段,但由于资源分布、地区经济发展不平衡和城市布局等因素的影响,我国集装箱货源分布和流向存在着很大差异,从而导致箱流在空间上、时间上的不平衡。空箱调运的好坏直接影响到运输成本及车辆、集装箱资源的使用效率。因此,空箱调运的研究,对于集装箱运输企业的实际运营具有重要的意义。同时集装箱空箱作为一种企业资源,其使用会给企业创造价值,但目前空箱调运模型大多只考虑调运成本最小,而忽视空箱变成重箱后所带来的效益。基于这些不足,本文建立基于“客户价值-调运成本”策略的铁路空箱调运模型,探索如何保证空箱转变成重箱后为企业创造的效益最大,即综合考虑集装箱能给企业创造的价值和相关调运成本,使空箱调运给企业带来的效益(价值减去成本)最大。
1 国内外研究成果及不足
1.1 研究成果及进展 White W.W.和Bomberault A.M.〔1〕是最早对集装箱运输问题进行研究的学者,他们通过构造一个“空间-时间”模型来描述现实中一定时间段内的集装箱空箱调运问题,并给出了时间间隔不确定条件下的诱导式网络流算法以及相应的计算例子。Williame C.Jordan和Mark A.Turnguist〔2〕建立了一个针对铁路运输系统中空货车分派的动态网络最优化模型。模型中包含了在一定计划期内,网络中各个节点上可能满足预期需求的潜在收益,以及不能满足这些需求的损失成本和为了满足预期需求而贮存空车的成本以及系统内调运空车的成本。Teodor Gabriel Crainic,Michel Gendreau 和Pierre Dejax〔3〕认为空箱的供给和需求都是动态和随机的,对这些随机变量可以进行确定化处理,于是建立了两阶段限制资源模型,但该模型只适用于单箱种,以线性规划为基础。
文献〔4〕对集装箱空箱产生的原因、空箱调运要解决的问题等进行了描述,根据集装箱业务流程,列出该流程影响空箱调运的诸多要素,并对这些要素进行假设处理,忽略一些次要因素,将它们设为变量或常量。然后以空箱调运的成本最小化为目标建立空箱调运模型,并对模型进行了求解。文献〔5〕从铁路集装箱运输市场的实际情况出发,设置相关的变量,建立基于顾客偏好的模糊运输规划模型和带时间窗的运输规划模型。
1.2 存在的不足 与空车调运类似,铁路集装箱办理站首先应使用本站卸空箱满足适箱货物需求。当一个车站的装箱数大于卸空箱数时,就需要接入空箱,相反则排出空箱。但由于集装箱数量有限,难以满足全部货物对空箱的需求,因此由哪些空箱供应站向哪些空箱需求站调运空箱,调运数量是多少就成为优化的核心问题。
铁路运输遵循先计划内后计划外,先重点后一般,先中央后地方的原则,其核心是在保证重点物资运输的基础上分轻重缓急,全面统筹安排运输任务。基于此要求,本文采用现代企业客户关系理论,将使用客户按价值高低分为不同的优先等级,在空箱调运方案中,首先满足高序位价值客户的需求,并在高序位价值客户的需求得到满足后仍有空箱时,才考虑低序位价值客户的空箱需求。
2 模型的建立
2.1 建模思路 基于“价值-成本”策略的空箱调运吸收了前人空箱调运研究的合理成分,同时又引入了新的优化目标,使空箱调运更加符合企业的生产实际,基本思路如下:
1)确定集装箱空箱的供给站和需求站,以及相关车站集装箱空箱的需求量和供给量;
2)对集装箱空箱需求客户进行分析,确定其客户价值的大小;
3)按照客户价值大小对客户进行分类,对属于同一类别的客户,按其空箱产生直接效益的大小再进行排序;
4)优先满足高序位客户的空箱需求,在同一序位中优先满足直接效益大的客户,依次类推;
5)调运以实现本次空箱调运产生的效益最大为最优;
6)由于客户的间接价值大小难以直接量化,本文把客户价值全部换算成直接价值。
2.2 客户价值分析 本文从我国铁路集装箱企业和目前客户关系管理的发展出发,基于客户价值对铁路集装箱客户划分为价值客户(I类)、次价值客户(II类)、潜价值客户(III类)和低价值客户(IV类)共4类(见图1所示)。同时,由于铁路运输具有公共产品的特性,在突发事件如抢险救灾物资运输时需优先满足,因此还存在一类特殊客户(S类)如政府、军队,虽然其具有弱经济性但在突发事件中必须优先满足。
“价值—成本”策略空箱调运模型的建立首先需要对铁路集装箱客户价值进行评价,然后对其进行客户分类。所构建的客户价值评价体系,从当前价值和潜在价值这2个维度来综合地评价一个客户的价值。当前客户价值的评价指标有利润、运输需求量和总运输服务成本;潜在客户价值的评价指标有市场价值、合作潜力、客户忠诚度和信用价值。
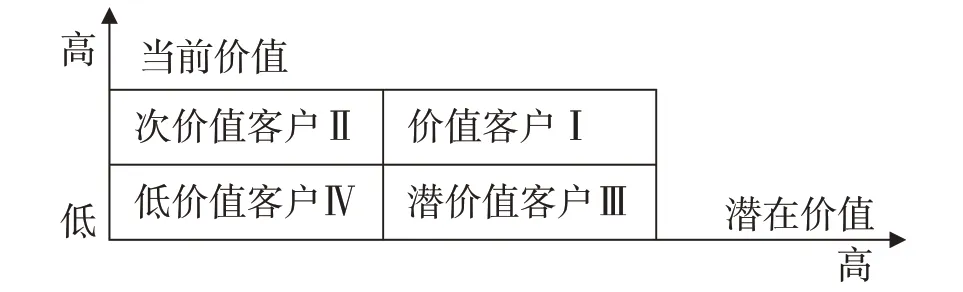
图1 铁路集装箱客户分类
2.3 假设条件 模型的基本假设如下:1)系统假定各期每个集装箱节点产生的空箱数量已知、每个节点的空箱需求量已知;2)系统封闭,当集装箱不足时不考虑从系统外调箱;3)不考虑转运现象,空箱直接从供应地运往需求地;4)模型只考虑单一运输方式,即集装箱节点之间只分析铁路运输方式;5)模型只研究单一箱型,不考虑集装箱不同箱型之间的混用、替换;6)空箱调运决策期为周,不考虑集装箱调运的运输时间限制;7)客户需求得不到满足是可以允许的;8)规定客户对空箱需求的满意度只有“满意”或“不满意”2 种,即当空箱在规定时间内送到就为满意,否则为不满意;9)假定突发事件下,如军运、抢险救灾等重点物资的特殊客户需求总是满足的。
2.4 参数与决策变量设置 模型中参数与决策变量设置如下:
1)系统中有m个空箱供给站(A1,…Ai,…,Am),供给量分别为ai(i=1,2,…m),总供给量;
2)系统中有n个空箱需求站(B1,…Bj,…Bn),需求量分别为bj(j=1,2,…n),总需求量;
3)cij为从Ai到Bj之间的单位空箱调运成本;
4)每一需求站Bj通常情况下的4类不同客户空箱需求量分别为(yj1,yj2,yj3,yj4);若存在突发事件,则假设第五类特殊客户(S类)的需求量为rjs;
5)xij为从集装箱供给站Ai到需求站Bj的实际空箱调运量;
6)通常情况下,每一需求站Bj的4 类不同客户数量分别为Qjk(k=1,2,3,4),k 表示客户分类数;其中客户价值为,ω为0 到Qjk之间的整数。突发事件下,特殊客户S的数量为Qjs,其客户价值为,o为0到Qjs之间的整数;
8)α为一个可变整数,其取值如下:

2.5 模型
2.5.1 目标函数
1)第一优化目标为空箱调运成本应极小化。
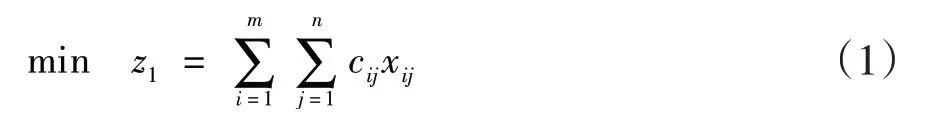
2)第二优化目标为集装箱使用后产生的总价值应极大化。

2.5.2 约束条件
1)满足缺少空箱的集装箱节点的需求。
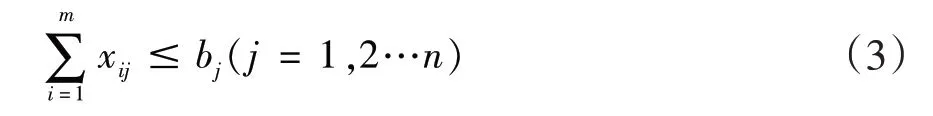
2)集装箱空箱供给站发送到集装箱需求站的空箱总和小于或者等于集装箱供给站可提供的空箱数量。
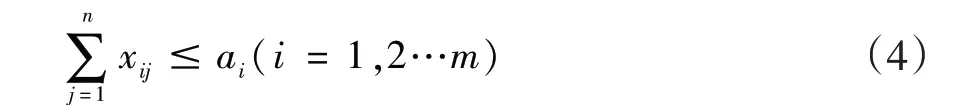
3)某一需求站所有不同类别客户实际分配到的空箱量等于本站所得到的空箱总量。

3 算例
3.1 已知条件 假设有7个集装箱办理站供应空箱,6个办理站需要空箱,各节点之间的空箱调运费用情况见表1;空箱供应节点发送空箱的情况见表2;空箱需求节点的空箱需求情况见表3。
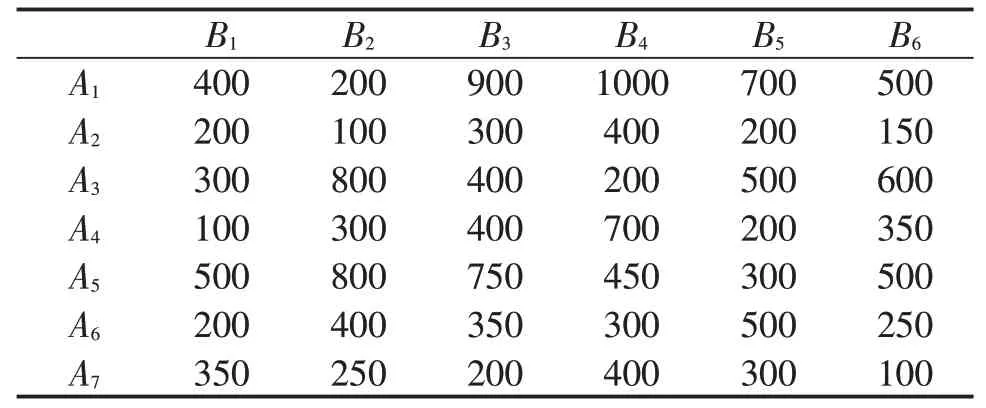
表1 系统内节点间单位空箱调运费用(元/箱)

表2 空箱供应情况表(箱)

表3 空箱需求情况表(箱)
采用模糊层次分析法是对空箱需求节点的客户价值进行评价,然后采用层次聚类分析法对已经评价好的客户进行分类。需求站客户分类情况与需求情况如下:
B1站S、Ⅰ、Ⅱ、Ⅲ、Ⅳ类客户空箱需求量为:5、10、10、5、5;
B2站S、Ⅰ、Ⅱ、Ⅲ、Ⅳ类客户空箱需求量为:0、10、0、5、5;
B3站S、Ⅰ、Ⅱ、Ⅲ、Ⅳ类客户空箱需求量为:0、5、5、0、5;
B4站S、Ⅰ、Ⅱ、Ⅲ、Ⅳ类客户空箱需求量为:0、5、5、5、0;
B5站S、Ⅰ、Ⅱ、Ⅲ、Ⅳ类客户空箱需求量为:0、10、5、0、0;
B6站S、Ⅰ、Ⅱ、Ⅲ、Ⅳ类客户空箱需求量为:0、5、0、5、0。
Ⅳ类客户空箱需求满足能产生的直接经济价值分布如下:
B1站:1000元(3箱)、2000元(2箱);
B2站:1500 元(2 箱)、1200 元(2 箱)、1400 元(1箱);
B3站:2000元(3箱)、1700元(2箱);
B4站、B5站、B6站均为0元。
3.2 结果分析 采用MATLAB 软件对模型进行求解,得到空箱调运方案:
A1站供应给B1、B2、B3、B4、B5、B6站的空箱数分别为:0、15、0、0、0、5;
A2站供应给B1、B2、B3、B4、B5、B6站的空箱数分别为:10、0、0、0、0、5;
A3站供应给B1、B2、B3、B4、B5、B6站的空箱数分别为:0、0、5、15、0、0;
A4站供应给B1、B2、B3、B4、B5、B6站的空箱数分别为:15、0、0、0、0、0;
A5站供应给B1、B2、B3、B4、B5、B6站的空箱数分别为:0、0、0、0、15、0;
A6站供应给B1、B2、B3、B4、B5、B6站的空箱数分别为:5、0、0、0、0、0、0;
A7站供应给B1、B2、B3、B4、B5、B6站的空箱数分别为:2、0、8、0、0、0、0。
从结果中可以看出,集装箱供应优先满足了S、Ⅰ、Ⅱ、Ⅲ类高序位客户的需求。
4 结束语
论文最主要的特点就是引入客户价值,将客户价值与调运成本结合起来研究集装箱空箱调运。对集装箱空箱的需求按照客户价值高低进行优先级划分,高序位的客户应尽量优先满足。这种调运策略从企业经营的角度出发,以实现企业效益最大化为目标,体现了现代市场营销的特点。将空箱调运和市场经营更加紧密地联系起来,比单一的考虑调运成本最小更具意义。并且算例表明,基于“价值-成本”策略的铁路空箱调运模型可以有效地得到优化方案,满足铁路运输的需要,为铁路运输提供科学合理的解决方案。
〔1〕White W.W.,Bomberault A.M.A Network Algorithm for Empty Freight Car Allocation〔J〕.IBM SystemJour⁃nal.1969,No.2:147~169.
〔2〕William C.Jordan,Mark A.Turnguist.A Stochastic Dynam⁃ic Network Model For Railroad Car Distribution〔J〕.Trans⁃portation Science.1983,5:123~145.
〔3〕Teodor Gabriel Crainic,Miehel Gendreau,Pierre Dejax.Dy⁃namie And Stochastic Models For The Allocation Of Empty Containers〔J〕.Operations Research.1993,l-2:102~126.
〔4〕赵宏舟.海运集装箱调度优化问题研究〔D〕.上海海运学院研究生论文.1991.12.
〔5〕张得志,谢如鹤,黄孝章.铁路集装箱空箱调度模型及求解算法〔J〕.中国铁道科学.2003.6:125~129.

