考虑降雨入渗的边坡稳定性分析

房 亮

(上海建筑设计研究院有限公司，上海 200041)

据统计，在国内大气降雨是绝大多数滑坡的主要促发原因。据调查分析，滑坡变形特征、位移速度与降雨量成正比关系［1］。但人们对降雨与滑坡关系认识的还不是很充分，因此深入研究降雨与滑坡关系并建立定量模型对滑坡的预报和预防都有重要指导意义。降雨对边坡产生影响的原因是雨水渗入边坡体内，导致孔隙水压力增大、含水量增加，从而使土体容重增加、强度下降，引起边坡失稳。目前对这一问题的研究主要采用数值方法，对雨水入渗引起的渗流场变化进行模拟，分析降雨强度、降雨持时、雨型、土体渗透性［2］、土体裂隙［3，4］等对渗流场的影响，并用极限平衡法研究上述因素对安全系数的影响。本文详细介绍了考虑雨水入渗时对极限平衡法进行了改进，并对土体抗剪强度参数、自重变化、初始状态对降雨时边坡稳定性的影响进行了分析。

1 降雨入渗引起的边坡的暂态渗流场与强度变化

在雨水入渗情况下土坡稳定性分析中，首先需要弄清楚降雨引起的渗流场的变化。在很多情况下饱和区与非饱和区水分的运动是相互联系的，因此将两者统一在一起，分析以压力水头为控制方程的因变量。

渗流控制方程为［5］:

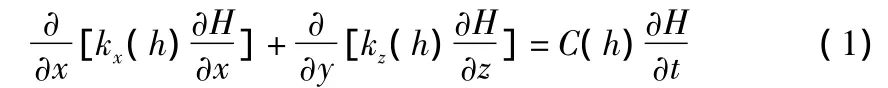
式中:H——总水头，H=h+z，h在饱和区为渗流压力水头为正值，在非饱和区为毛细管压力水头为负值，z为位置水头;

kx——土体水平方向的渗透系数;

kz——土体垂直方向的渗透系数;

C(h)——比水容重。

边界条件是解决问题的关键之一，本文降雨入渗的上边界采用流量边界条件，下边界为不透水边界，左右边界地下水位以下采用定水头边界，地下水位以上采用不透水边界。

本文采用有限体积法对方程(1)进行求解［3］。求出边坡体中各点的孔隙水压力后根据土水特征曲线可得各点的体积含水量，同时可得土体的抗剪强度。

非饱和土的抗剪强度场采用Fredlund提出的双应力变量抗剪强度公式:

其中，c'，φ'均为有效应力强度参数;φb为随基质吸力变化的内摩擦角。当孔隙水压力为正值(uw≥0)时，令φb=φ'，则非饱和土抗剪强度公式就变成了饱和土抗剪强度公式。

2 饱和—非饱和土边坡稳定性分析模型

在实际工程的边坡设计过程中，边坡稳定性分析均采用极限平衡法进行计算，Bishop法是较常用的一种极限平衡条分法［6］。Bishop法假定条块间只有水平作用力Ei，如图1所示。

若条块处于静力平衡状态，根据竖向力平衡条件，有:

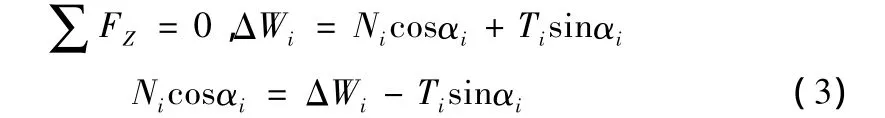
根据满足安全系数为Fs时的极限平衡条件:

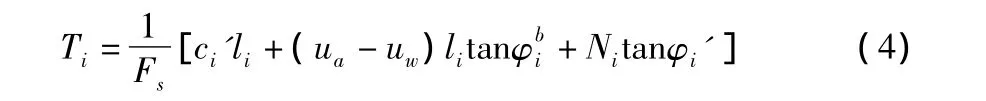
由式(3)，式(4)整理得:

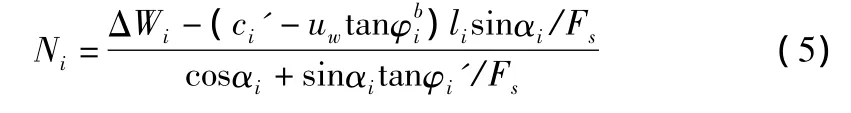
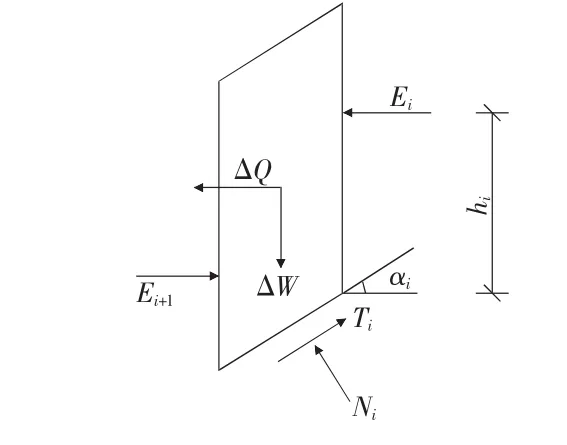
图1 Bishop法作用力分析

考虑整个滑动体的整体力矩平衡［6］:

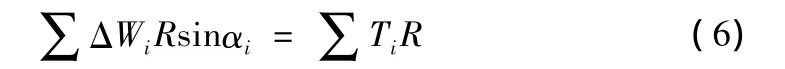
将式(4)～式(6)联立简化得:

式(7)就是降雨入渗条件下饱和—非饱和土坡稳定的Bishop法计算公式。该式中当uw≥0时φb=φ'，这样就将饱和区与非饱和区统一在一个公式中。

降雨入渗情况下，每个土条的自重会变化。土条重量与体积含水量关系为［7］:

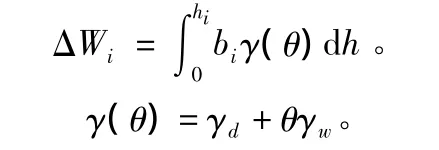
其中，γd为土的干容重;γw为水容重;θ为体积含水量。根据式(1)求出土中各点的孔隙水压力后再根据土水特征曲线得到各点体积含水量，从而可得土条自重的变化。

为了便于式(7)在边坡稳定计算中的应用，令:

将与水压力有关的项并入凝聚力项，这样就可以直接应用常规的边坡稳定分析程序计算安全系数。其不同点在于，各个土条的自重会随时间变化，土体中各点的孔隙水压力变化造成C也随时间变化。

3 计算模型及参数选取

本文计算边坡形状如图2所示。边坡厚度30 m，FED为不透水边界，GH为地下水位线，坡面BC倾角15°，FE长度30 m，ED水平面投影为150 m。MN为边坡上给定的滑裂面。土体饱和渗透系数为2×10－6m/s，属于典型的粉土，渗透性比较好;降雨强度10－6m/s;降雨历时为24 h。

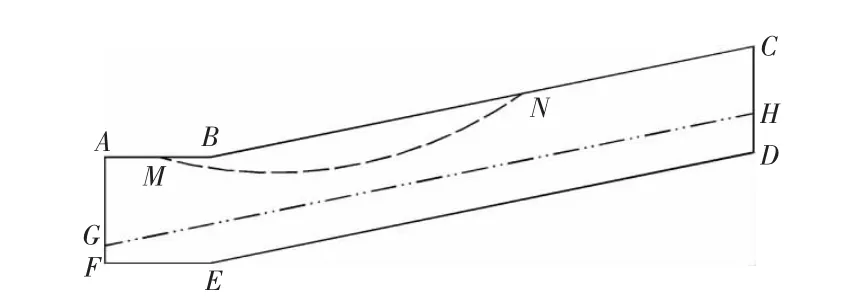
图2 计算边坡

本文分析非饱和土的渗透系数与基质吸力关系按Gardner［8］的经验公式确定:

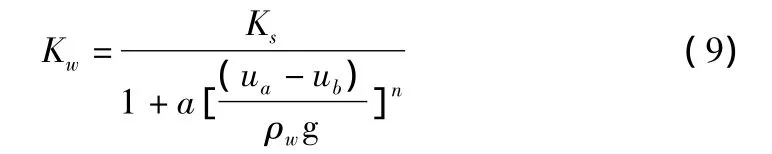
其中，Kw为非饱和土的渗透系数;Ks为饱和土的渗透系数;(ua－ub)为土的基质吸力;ρw为水的密度;a，n均为试验常数，本文分别取 0.1，2。

对土体的土水特征曲线，采用包承纲等［9］建议的对数方程表如下:

其中，θ为土体的体积含水量;a，b均为拟合参数，本文分别取 0.505 3，0.082 6。

土体的重度和抗剪强度参数取值如下:

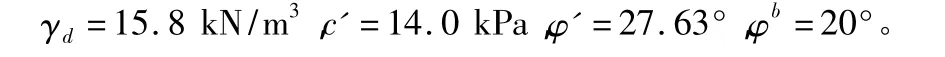
4 边坡稳定影响因素敏感性分析

根据前面的分析，编制了降雨入渗条件下计算边坡渗流场的程序和基于Bishop法的求解指定滑裂面饱和—非饱和统一的边坡安全系数程序，对边坡稳定主要影响因素进行敏感性分析。

4.1 抗剪强度参数

抗剪强度参数c'，φ'随土体含水量的增加会减小，含水量对c'值影响较大，对φ'影响较小［8］;一些试验结果表明:φb也会随含水量变化，随含水量增加而增大，当土体饱和时增大为φ'。因此对抗剪强度进行敏感性分析可以加深参数变化对安全系数影响的认识。图3是在没有考虑降雨条件下，对给定滑裂面改变抗剪强度参数值所得计算结果。

图3 抗剪强度参数与安全系数

从图3中可以看出，安全系数Fs与c'，φ'，φb呈线性关系。φ'的影响最大，c'影响最小。φ'每增加1°，安全系数约增加 0.09;φb每增加1°，安全系数约增加0.07;c'每增加1 kPa，安全系数约增加0.03。如果在降雨入渗情况下将各参数假定为常数进行稳定性分析很可能造成错误的预测，因此对各参数含水量变化规律及在安全系数计算中运用是亟待解决的问题。

4.2 土体自重变化

在不考虑抗剪强度参数变化的情况下，降雨对边坡稳定性的影响主要是土体自重增加提高下滑力、孔隙水压力增加减小抗滑力。土体自重变化对边坡稳定性影响如图4所示。

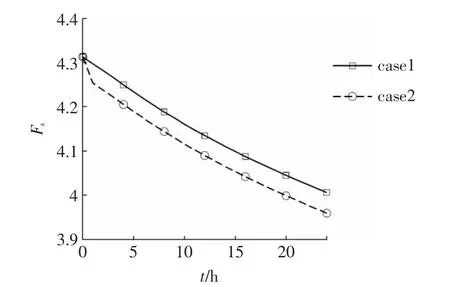
图4 土体自重变化对安全系数影响

case1为假定土体自重不变仅考虑孔隙水压力变化时安全系数的变化情况，case2为考虑降雨造成土体自重增加时随降雨进行边坡安全系数的变化。考虑自重变化24 h降雨使安全系数降低0.353，即考虑孔压变化安全系数降低0.306，自重的增加对安全系数影响占13.3%。可见在降雨入渗情况下，对边坡稳定性其主要的作用是孔隙水压力的变化。

4.3 土体初始渗流场

不同季节不同前期雨量条件下，同一边坡相同降雨对边坡稳定性的影响也是不同的，这说明土体的初始渗流场对边坡的稳定性分析同样十分重要。本文给出两种不同地下水位情况下的初始渗流场，给定相同降雨情况，安全系数变化规律如图5所示。

图5 不同地下水位对安全系数影响

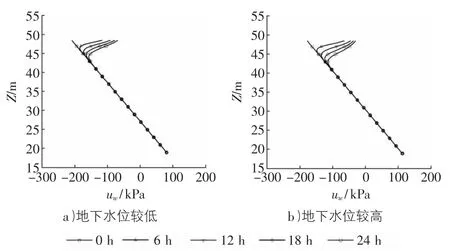
图6 某断面孔隙水压力随降雨变化

case1为地下水位较低情况，case2为地下水位较高情况。从图5中可以看出，地下水位较高时，初始安全系数较低，并且随着降雨的进行安全系数降低更多。其机理是:地下水位较高时，边坡各点初始含水量较大，土体重量较大，基质吸力较小，从而初始安全系数较小;初始含水量越高，湿润区推进越快，如图6所示，降雨影响范围越深，安全系数降低越多。所以初始渗流场对边坡稳定性分析有很大的影响，各点初始含水量越高，对边坡稳定性越不利。

5 结语

本文通过采用暂态饱和—非饱和渗流有限体积法与边坡稳定性极限平衡分析相结合的方法，对降雨入渗导致的边坡稳定性变化进行了敏感性分析，初步得到如下认识:

1)抗剪强度参数对边坡稳定性影响比较敏感，其中φ'是影响最大的。

2)降雨对边坡稳定性的影响主要是孔隙水压力变化造成的，土体自重变化影响相对较小。

3)初始渗流场不同，相同降雨条件下边坡安全系数变化情况也不相同，在对边坡进行稳定性分析时，初始渗流场的确定很重要。

［1］朱文彬，刘宝琛.公路边坡降雨引起的渗流分析［J］.长沙铁道学院院报，2002，20(6):104-108.

［2］吴宏伟，陈守义，庞宇威.雨水入渗对非饱和土坡稳定性影响的参数研究［J］.岩土力学，1999，20(1):1-14.

［3］范 平，刘青泉，孙建平，等.带裂隙边坡的降雨入渗规律数值模拟研究［J］.中国科学，2009(10):37-38.

［4］姚海林，郑少河，李文斌，等.降雨入渗对非饱和膨胀土边坡稳定性影响的参数研究［J］.岩石力学与工程学报，2002，21(7):1034-1039.

［5］雷志栋，杨诗秀，谢森传.土壤水动力学［M］.北京:清华大学出版社，1988.

［6］陈仲颐，周景星，王洪瑾.土力学［M］.北京:清华大学出版社，1994.

［7］张士林，王冬梅，李根华.非饱和土坡危险含水量分析［J］.中国工程科学，2004，5(6):71-75.

［8］Gardner W R，Fireman M.Laboratory studies of evaporation from soil columns in the presence of a water table，Soil Sci，1958(85):244-249.

［9］Frendlund D G，Xing A.Equations for thesoil-water characteristic curve［J］.Can Geotech J，1994(31):521-532.

［10］姚裕春，姚令侃，袁碧玉.降雨条件下边坡破坏机理离心模型研究［J］.中国铁道科学，2004，25(4):64-68.