谈基坑开挖安全系数的影响因素

钱玉林 李小伟 王飞艳

(1.扬州大学建筑科学与土木工程学院，江苏扬州 225127;2.常州市建筑科学研究院有限公司，江苏常州 213000)

0 引言

随着我国经济建设的快速发展，城市化水平越来越高，高层建筑大量兴建。商业用房，车库等加速了地下空间的开发，在这些工程中遇到一个普遍问题就是基坑开挖过程中边坡稳定问题，这一问题一直是土木工程学科中重要研究课题。本文结合工程实例，对土体强度指标c，φ值以及地下水位对基坑开挖过程中边坡稳定的影响进行分析比较［1］。

1 工程概况

广福花园小区位于扬州市广陵区，人民路与秦邮路交叉口，基坑形状不规则，东西走向，东西向长268 m，南北向长83 m，基坑总面积15 080 m2，本工程人防地下室±0相当于1985年国家高程+7.70 m(绝对高程)，地下室顶板高程为－5.4 m(相对高程)，板厚0.40 m，垫层厚0.15 m，地面整平后的平均高程为 +6.85 m(绝对高程)，实际基坑开挖深度为5.10 m。

本工程基坑支护方案根据总平面图、基础图、地质条件并结合周边建筑物分布情况及基础型式确定，基坑侧壁安全系数等级为三级，侧壁重要性系数为0.9，各侧均采用三级放坡支护方案，放坡各侧基坑坡面均采用φ6钢筋网片(200 mm×200 mm)C20喷射细石混凝土(厚8 cm)护坡。基坑地下水位线在3.5 m，采用二级轻型井点降水。

根据岩土工程地质勘察报告，得到该基坑所处地层情况及强度指标见表1。

2 瑞典条分法

瑞典圆弧法的基本假定:

1)假定土坡稳定问题是平面应变问题。

2)假定滑裂面为圆弧形，计算时不考虑土条两侧的作用力。

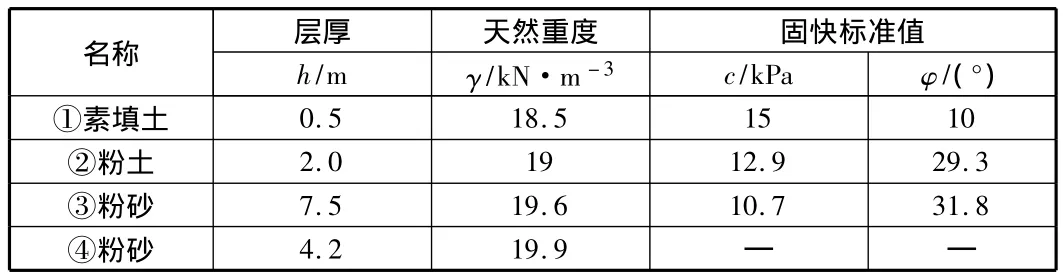
表1 土层物理参数

3)假定计算圆弧面上的安全系数值K时，简单地将条块重量向滑面法向分解来求得法向力。

由于弧面上各点的斜率都不相等，自重等外荷载对弧面的法向和切向作用分力都不能按整体计算，所以采用条分法计算，如图1所示［2，3］。

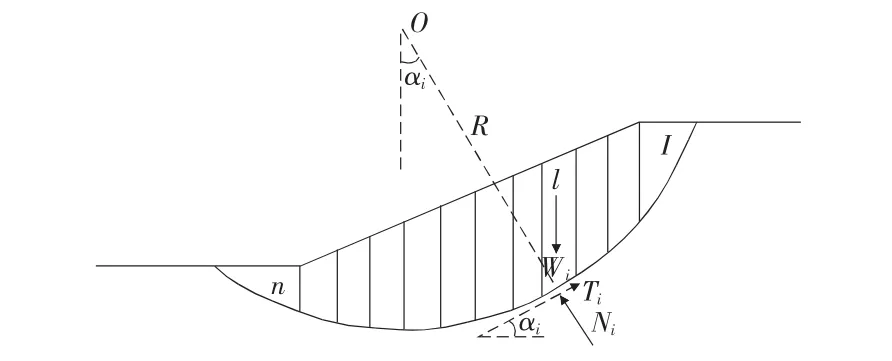
图1 瑞典条分法受力分析图示

依据假定用附加外力使土坡达到极限平衡，安全系数的计算公式如下:

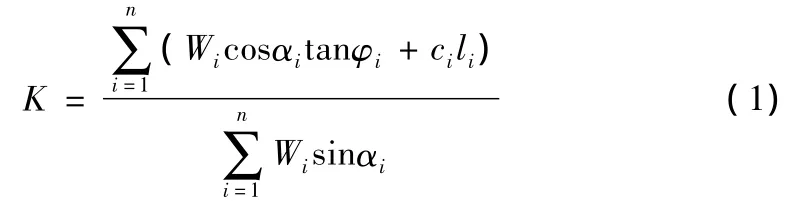
3 边坡稳定影响因素分析

边坡的稳定受各种因素的影响，如地下水位、土体的强度指标等。因此讨论地下水位，c，φ值的变化对边坡稳定，对实际工程有重大意义。

3.1 c值变化对边坡稳定的影响

由于本工程中土层①，②厚度较小，在原有的计算基础上，保持其他条件不变，将土层③的 c值相应变化 ±5%，±10%，±15%，±20%，其他条件也不变。利用瑞典条分法计算得到结果见表2;将数据整理得出安全系数随c值的变化曲线，如图2所示。

表2 安全系数随c值的变化

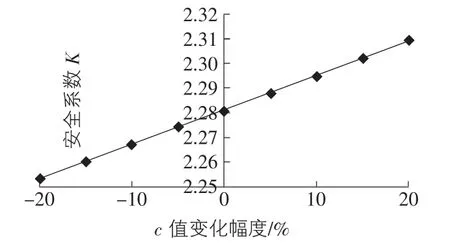
图2 安全系数K随c值变化曲线

由图2分析可得，安全系数K随粘聚力c值的增大而增大。

3.2 φ值变化对边坡稳定的影响

在原有的计算基础上，保持其他条件不变，将土层③的φ值相应变化±5%，±10%，±15%，±20%，其他条件也不变。利用瑞典条分法计算得到结果如表3所示;数据整理得安全系数随φ值的变化曲线，见图3。

表3 安全系数随φ值的变化

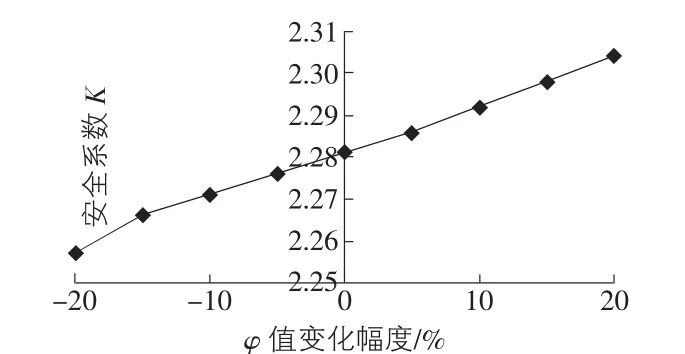
图3 安全系数K随φ值变化曲线

由图3可知，安全系数随土体φ值的增大而增大。

3.3 边坡稳定中c，φ值敏感性分析

敏感度系数是指评价指标变化的百分率与不确定因素变化百分率之比。敏感度系数越高，表示对该不确定因素的敏感度越高。敏感度系数的计算公式为:

式中:SAF——指标A对于不确定性因素F的敏感度系数;

ΔF/F——不确定因素F的变化率;

ΔA/A——指标A的变化率。

对滑动面进行计算，得到c，φ值敏感性分析结果如表4，表5所示。

表4 稳定安全系数对于c的敏感度系数

表5 稳定安全系数对于φ的敏感度系数

由表4，表5分析可得土体的c值比φ值对边坡稳定影响大。

3.4 地下水位的影响

由于该工程濒临长江，地下水位高，在边坡稳定分析过程中对地下水位影响进行简要分析，分别取基坑外侧地下水位为2 m，2.5 m，3 m，3.5 m，4 m，4.5 m 时，对边坡稳定安全系数进行比较。利用瑞典条分法计算得到结果如表6所示。

表6 稳定安全系数随地下水位的变化

由计算结果分析可得:安全系数随基坑外侧地下水位的降低而相应的增大。

4 结语

本文以瑞典条分法为理论基础，分别讨论地下水位、强度指标c，φ值对边坡稳定的影响，得到以下几点结论:1)在一定范围内，基坑开挖安全系数K随c，φ值的增大而增大。2)通过敏感性因素分析理论，分别把c，φ值作为不确定因素进行讨论分析，比较敏感度系数，得出c值对边坡稳定的影响比φ值大。3)通过计算基坑外侧地下水位在不同位置的稳定安全系数，分析比较得出基坑外侧地下水位越低，基坑开挖安全稳定系数就越高。

［1］杨庚宇，赵少飞.土坡稳定分析圆弧滑动法的解析解［J］.工程力学，1998(sup):440-443.

［2］卢廷浩，高贵全.有效应力概念下瑞典条分法稳定安全系数公式讨论［J］.水利水电科技进展，2011，3(2):43-45.

［3］杨 剑.瑞典条分法和毕肖普法在土坡稳定分析中的应用和研究［J］.盐城工学院学报，2005，18(2):66-68.