近地面强风不同间隔滑动平均统计特性的对比分析
史文海,李正农,吴建佳
(1.温州大学 建筑与土木工程学院,浙江 温州 325035;2.湖南大学 土木工程学院,湖南 长沙 410082)
0 引 言
风荷载是作用于工程结构上的主要载荷之一,只有比较准确地了解强风的特性及其变化规律,在估算风对结构的作用和进行风场模拟时才可能有较高的精度。近年来,我国许多学者在上海、广东和浙江等省开展了大量的近地边界层风场特性的实测研究,取得了较为丰硕的研究成果[1-15]。
在对风场特性进行统计分析时,我国普遍采用10min时距[7-8],且众多的研究者在进行风场特性分析时都采用10min离散平均的方式计算出相应的风场特性。然而,目前对风场数据处理方法的研究还较少,基于10min离散平均的统计分析方法对实测数据的利用远不充分,其结果不能很好的反映出风场的脉动性和变化规律,尤其是在实测风场数据较少的时候缺陷尤为明显。
文中基于两次台风风场的实测数据,以3s、10s、1min和10min为间隔,进行了强风特性的10min滑动平均统计特性对比分析,以期获得对近地面强风风场特性及其数据处理方法的新认识。
1 风场数据介绍
本文以2008年7月实测获得的台风“海鸥”和“凤凰”的风场数据进行分析,其中台风“海鸥”于18日18时在福建长春镇登录,登陆时中心附近最大风力为10级(25m/s);台风“凤凰”于28日22时在福建东瀚镇登录,登陆时中心附近最大风力为12级(33m/s)。两次台风过程的部分观测数据相关说明见表1。

表1 观测数据说明Table 1 Field measurement specifications
近地风场观测点设置在温州大学建工楼顶部,属于城市市郊地形。在建工楼5层楼顶同一高度设置了两台WJ-3型风速风向仪,将其分别固定在9m高的直杆上(避免风速仪处风场受建工楼干扰)。两风速仪离地总高度约为30m,水平相距约17m。采用DH-5937数据采集系统进行数据采集,采样频率为20Hz。
2 不同间隔滑动平均法
2.1 滑动平均法
在动态测试数据中,对确定性成分和不确定成分进行分离时,如若只要消除动态测试数据中的随机起伏,而无需用某种函数或某些函数之和的形式来表示其变化规律,可采用平滑与滤波的数据处理方法,即滑动平均法来实现。该方法虽然是一种古典的数据处理方法,但在试验数据处理中经常被采用。
假定动态测试数据y(t)由确定性成分f(t)和随机性成分e(t)组成,且前者为所需的测量结果或有效信号,后者为随机起伏的测试误差或噪声。经离散化采样后,可相应地将动态测试数据写成

为了精确地表示测量结果,抑制随机误差e(i)的影响,常对动态测试数据y(i)作平滑和滤波处理。如对非平稳的数据y(i),在适当的小区间上近似为平稳的,而作某种局部平均,以减小e(i)所造成的随机起伏。这样对沿全长N个数据以某一拟定的滑动间隔在逐一小区间上进行不断的局部平均,即可得出较平滑的测量结果f(i),而滤掉频繁起伏的随机误差[16]。其中,滑动间隔的大小对数据的处理结果有较大的影响。
2.2 基于滑动平均法的风场统计特征分析
众多的研究者在进行风场特性分析时都采用10min离散平均的方式计算出相应的风场特性,即将风场数据根据时间序列按10min一段分成若干段(各段数据无重合),然后进行统计分析,以减小或消除测试误差、噪声以及短时距脉动的影响,得到风场的统计特征。但分析表明10min离散平均的统计分析结果不能很好的反映出强风风场的脉动性和变化规律,尤其是在实测风场数据较少的时候缺陷尤为明显,如绘制出来的结果图形数据点较少,不能连续地反映出风场的变化情况和脉动规律等。
因滑动平均法可有效地消除动态测试数据中的随机起伏得到较为平滑的测量结果,是一种简便而常用的数据处理方法。在此,为了解决10min离散平均进行风场特性统计分析的不足,本文提出采用滑动平均法对近地强风特性进行统计分析。如以10min为基本时距,将实测风场数据根据时间序列以某一时距为间隔进行滑动平均。如以1min间隔进行10min时距滑动平均时,截取的第一段数据即为0到10min之间的时间序列,第二段数据即为1min到11min之间的时间序列,依此类推。为了研究不同滑动间隔的影响,本文将以3s、10s、1min和10min为间隔进行滑动平均对比分析,其中以10min为间隔进行滑动平均实际上与10min离散平均方法相同。
3 近地面强风滑动平均统计特性对比分析
以下对实测获得的台风“海鸥”和“凤凰”的风场数据,以3s、10s、1min和10min为间隔,进行近地面强风特性的10min滑动平均的对比分析,其中风场参数(如平均风速和风向角、湍流度、阵风因子和湍流积分尺度)的相关定义及计算公式详见文献[6-7]。限于篇幅,文中只给出了部分对比分析图形和结果分析。
3.1 平均风速和风向角
图1~图3给出了台风“海鸥”和“凤凰”以3s、10s、1min和10min为滑动间隔的部分10min平均风速和风向角时程。结果表明,以3s、10s和1min为间隔的滑动平均对实测风场数据利用更加充分,如计算出的10min平均统计值更多,图像连续性非常好,能较好地反映出平均速度、风向角随时间的连续变化趋势和短时段内的脉动规律,从而更加充分地揭示出近地强风平均风速和风向角的统计特性和脉动规律。相对而言,从10min滑动平均图形很难获得相应的规律。
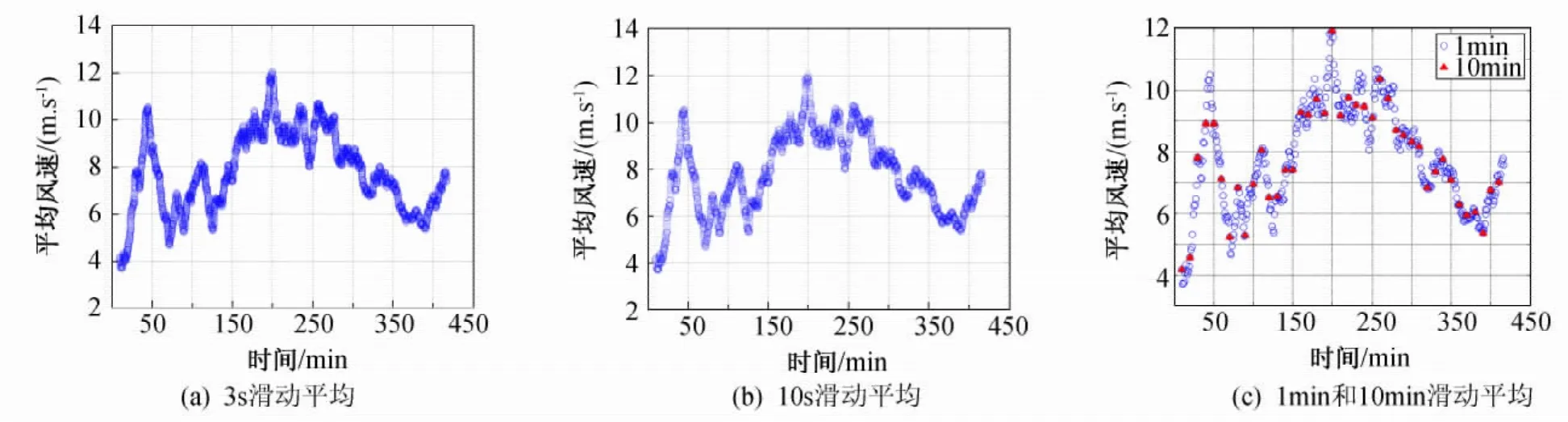
图1 台风“海鸥”的平均风速时程Fig.1 Mean wind speed time series of typhoon Kalmaegi
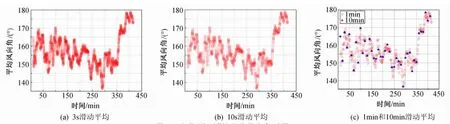
图2 台风“海鸥”的平均风向角时程Fig.2 Mean wind direction time series of typhoon Kalmaegi
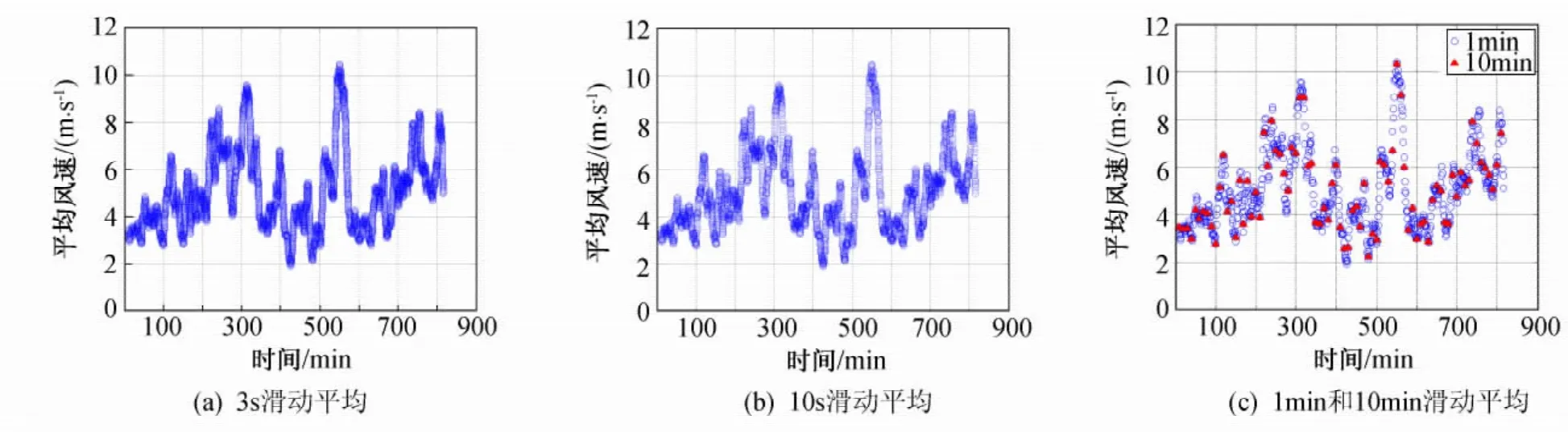
图3 台风“凤凰”的平均风速时程Fig.3 Mean wind speed time series of typhoon Fung-wong
另外,从图1~图3中可以看出,3s、10s滑动平均与1min滑动平均的连续性基本一致,都能很好的反映出10min平均风速、风向角随时间的变化规律。因1min滑动平均的计算量要比3s、10s滑动平均的计算量小许多,所以在进行风场统计特性分析时采用1min滑动平均方法更加简洁。
3.2 湍流度
湍流度反映了风的脉动强度,为确定结构所受脉动风荷载的关键参数。图4~图6给出了两次台风以10s、1min和10min为滑动间隔的部分10min时距的顺风向和横风向湍流度时程。由前述平均风速和风向角的对比分析可知,以3s滑动间隔计算得到的结果非常密集,此处及下文不再给出。图4~图6结果表明,10min滑动平均图形中湍流度结果连续性差,很难反映出湍流度短时段内的变化趋势及其脉动规律;以10s和1min滑动平均的湍流度脉动非常连续,且具有一定的周期性,较好地反映出了湍流度在不同时刻的变化趋势和脉动规律,从而使研究人员获得对风场湍流特性更加清晰的认识。
图7给出了台风“海鸥”以10s、1min和10min为滑动间隔的10min时距的顺风向湍流度与平均风速的关系。图7结果表明,10min滑动平均图形中湍流度结果的数据点少、分布范围小,其反映出的湍流度随平均风速的变化趋势和分布特征没有10s和1min滑动平均结果好。尤其是在平均风速较大时因数据点太少,10min滑动平均结果基本不能反映出湍流度随平均风速的变化规律。因强风的持续时间往往较短,而短时距滑动平均对实测风场数据利用更加充分,计算出的数据点多而密集,且其结果具有较好的连续性,从而能较好的揭示出风速较大时湍流度随平均风速的变化规律。风速越大对建筑结构的作用也越大,所以风速较大时湍流度随平均风速的变化规律往往对工程结构的抗风设计非常重要。

图4 台风“海鸥”的顺风向湍流度时程Fig.4 Longitudinal turbulence intensity series of typhoon Kalmaegi
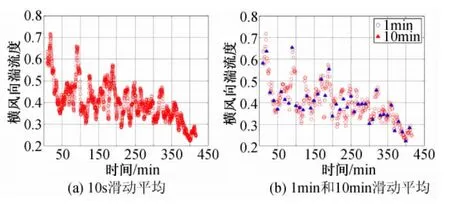
图5 台风“海鸥”的横风向湍强度时程Fig.5 Lateral turbulence intensity series of typhoon Kalmaegi
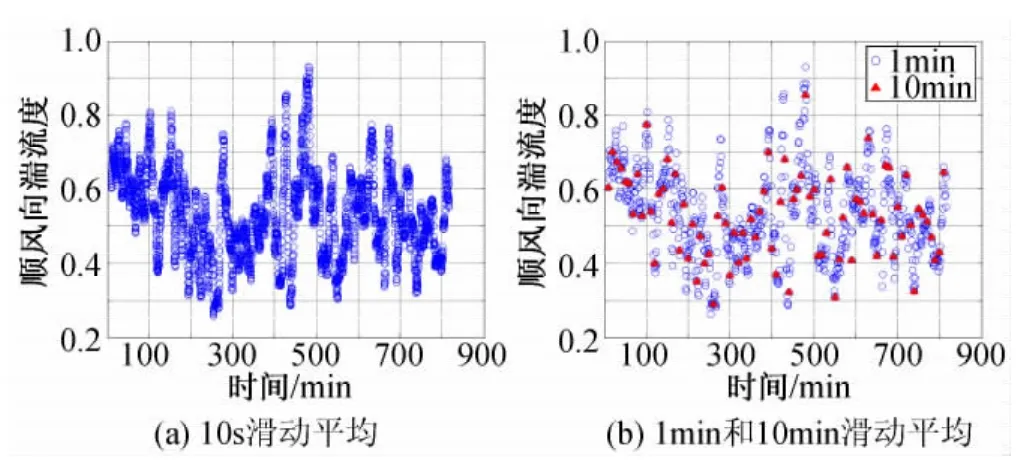
图6 台风“凤凰”的顺风向湍流度时程Fig.6 Longitudinal turbulence intensity series of typhoon Fung-wong

图7 台风“海鸥”的顺风向湍流度与10min平均风速的关系Fig.7 Relationship between longitudinal turbulence intensity and 10min mean wind speed during typhoon Kalmaegi
另外,图4~图7结果也表明,10s滑动平均与1min滑动平均的连续性基本一致,因1min滑动平均的计算量要比10s滑动平均小,所以在进行风场湍流度统计特性分析时1min滑动平均方法更加简洁。
3.3 阵风因子
风的脉动强度也可用阵风因子来表示。图8给出了台风“海鸥”以10s、1min和10min为滑动间隔的10min时距的顺风向阵风因子时程。总体看来,三种不同滑动平均的阵风因子的均值基本相同,但是三种不同滑动平均的最大值却有较大差别。如台风“海鸥”最大顺风向阵风因子的10min滑动平均值分别比10s和1min滑动平均值小了18.4%和14.5%。另外,对比10s、1min和10min滑动平均的结果,也可以获得与湍流度的不同间隔滑动平均统计特性对比中相似的结果。横风向阵风因子的不同间隔滑动平均统计特性对比分析也能获得相似的结果。
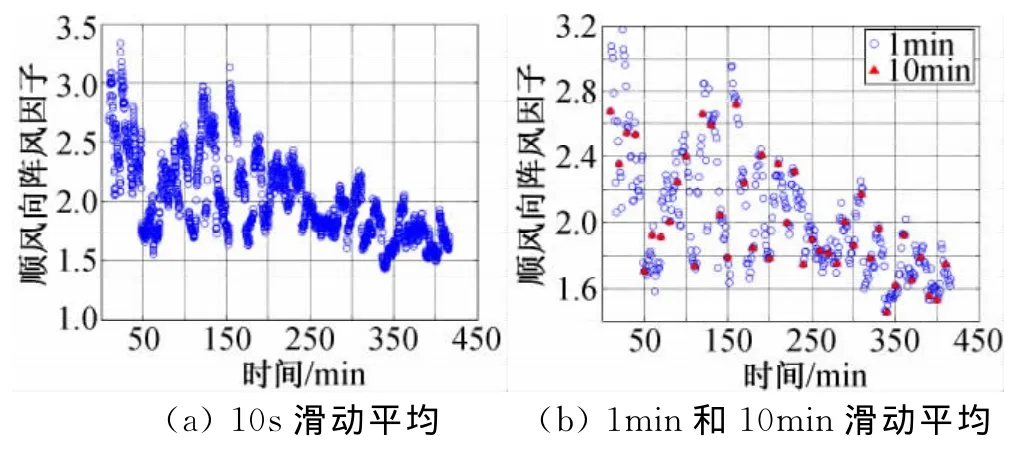
图8 台风“海鸥”的顺风向阵风因子时程Fig.8 Longitudinal gust factor series of typhoon Kalmaegi
3.4 湍流积分尺度
湍流积分尺度是脉动风中湍流涡旋平均尺寸的量度,湍流积分尺度也是反映风场特性的一项重要指标。考虑到进行3s和10s滑动平均求解湍流积分尺度的计算量较大,图9和图10仅给出了台风“海鸥”的1min和10min滑动平均的顺风向与横风向湍流积分尺度时程及其与平均风速之间的关系,其中湍流积分尺度根据Von Karman谱拟合实测风速谱得到[6]。图9结果表明,相比10min滑动平均结果,1min滑动平均求得的湍流积分尺度的分布范围更广,图像连续性较好,能较好地反映出湍流积分尺度随时间的连续变化趋势和短时段内的脉动规律。图10结果表明,1min滑动平均求得的结果较密集,能较好地揭示出风速较大时湍流积分尺度与平均风速的关系及其变化规律。

图9 台风“海鸥”的湍流积分尺度时程Fig.9 Turbulence integral length scale series of typhoon Kalmaegi
3.5 湍流功率谱密度函数
脉动风速功率谱密度函数可以用来描述脉动风的特性,其在频域上的分布可以描述湍流动能在不同尺度水平上的能量分布比例。基于前述风场特性的对比分析可知,基于不同时间间隔的滑动平均法对脉动风速功率谱进行对比分析时,也将获得脉动风速功率谱沿着风场时程的连续变化规律以及在不同湍流度和风速情况下的特征,从而获得对其新的认识。但基于不同时间间隔的滑动平均法对脉动风速功率谱进行对比分析时,需要非常多的结果图形才能完成,所以文中没有给出相关结果图形的对比和分析。
4 结 论
基于2008年影响温州地区的台风“海鸥”和“凤凰”的实测风场资料,以3s、10s、1min和10min为间隔,进行了近地面强风10min滑动平均统计特性的对比分析。研究结果表明,相对于以10min为间隔的滑动平均,以3s、10s和1min为间隔的滑动平均对实测风场数据利用更加充分,其结果具有更好的连续性,能较好地反映出平均速度、风向角、湍流度、阵风因子、湍流积分尺度和脉动风速功率谱密度函数随时间的变化趋势和短时段内的脉动规律,能较好的揭示出风速较大时湍流度、阵风因子、湍流积分尺度和脉动风速功率谱密度函数随平均风速的变化规律,从而更加充分的揭示出近地强风的统计特性。3s、10s滑动平均与1min滑动平均的连续性基本一致,因1min滑动平均的计算量小,在进行风场统计特性分析时1min滑动平均方法更加简洁。
[1]庞加斌,林志兴,葛耀君.浦东地区近地强风风特性观测研究[J].流体力学试验与测量.2002,16(3):32-39.
[2]LI Q S,XIAO Y Q,FU J Y,et al.Full-scale measurements of wind effects on the Jin Mao Building[J].Journal ofWindEngineeringandIndustrialAerodynamics,2007,95(6):445-466.
[3]FU J Y,LI Q S,WU J R,et al.Field measurements of boundary layer wind characteristics and wind-induced responses of super-tall buildings[J].JournalofWind EngineeringandIndustrialAerodynamics,2008,96(8/9):1332-1358.
[4]陈丽,李秋胜,吴玖荣,等.中信广场风场特性及风致结构振动的同步监测[J].自然灾害学报,2006,15(3):169-174.
[5]戴益民,李正农,李秋胜,等.低矮房屋的风载特性:近地风剖面变化规律的研究[J].土木工程学报,2009,42(3):42-48.
[6]史文海,李正农,张传雄.温州地区近地强风特性实测研究[J].建筑结构学报,2010,31(10):34-40.
[7]史文海,李正农,张传雄.温州地区不同时距下近地台风特性观测研究[J].空气动力学学报,2011,29(2):211-216.
[8]史文海,李正农,秦良忠,等.近地面与超高空台风风场不同时距湍流特性对比分析[J].建筑结构学报,2012,33(11):18-26.
[9]史文海,李正农,罗叠峰,等.台风“鲇鱼”作用下厦门沿海某超高层建筑的风场和风压特性实测研究[J].建筑结构学报,2012,33(1):1-9.
[10]郅伦海,李秋胜,胡非.城市地区近地强风特性实测研究[J].湖南大学学报(自然科学版),2009,36(2):8-12.
[11]李秋胜,戴益民,李正农,等.强台风“黑格比”登陆过程中近地风场特性[J].建筑结构学报,2010,31(4):54-61.
[12]宋丽莉,吴战平,秦鹏,等.复杂山地近地层强风特性分析[J].气象学报,2009,67(3):452-460.
[13]黄世成,周嘉陵,王咏青,等.两次台风过程近地层湍流度和阵风因子分析[J].气象科学,2009,29(4):454-460.
[14]申建红,李春祥.强风作用下超高层建筑风场特性的实测研究[J].振动与冲击,2010,29(5):62-68.
[15]陈凯,余永生,贾丛贤.傍山地区的强风场特性实测研究[J].流体力学实验与测量,2003,17(3):18-22.
[16]裴益轩,郭民.滑动平均法的基本原理及应用[J].火炮发射与控制学报,2001,1:21-23.

