轨道交通——站间距优化模型在郑州市地铁建设中的应用

张兴华 周 翔

（郑州大学 水利与环境学院，河南 郑州 450001）

地铁作为一项投资巨大且在城市交通中起骨干作用的城市客运交通系统，其站间距设置的大小，不仅与车站位置的设定有关，而且还关联到地铁的运营速度、工程投资以及社会效益等诸多方面。传统的站间距优化模型多以乘客出行时间为最小优化目标，建立站间距的简化优化方法，其求解结果比较有局限性。本文采用的以轨道线路系统的总成本（乘客出行时间、车站建设成本、运营成本）最小为优化目标，考虑客流量随车站间距的概率分布来建立最优站间距优化模型，对郑州市轨道交通站间距进行评价并提供理论指导。

1 模型具体表达式

本文采用轨道交通站间距优化的示意图及模型表达式如下（建立过程参考文献[1]）：

模型表达式

其中：第i年轨道线路所有乘客的平均出行时间；：乘客流随乘坐区间的概率分布；b：轨道交通线路的吸引带半径；d：最优站间距；：行人的平均步行速度；n：该路段有n个车站；s：列车每一站的平均停车时间；：列车的平均运行速度；：乘客流随乘坐区间的概率分布；：泊松分布参数，可以通过平均乘行距离来求，即有λ=/d；：乘客平均乘行距离；k：指乘客乘坐k个区间；和：d的约束条件，即最大间距和最小间距；int：取整函数。

2 模型求解及1、2号线站点设置的合理性评价

1）模型求解及结果分析

本文采用Visual C++编程，通过模拟搜索的方法（在车站的最小间距与最大间距之间搜索,每搜索一次车站间距增加10m），得出最优间距的理论值，最后结合实际对其进行调整。

计算参数：1号线长度=n.d=26.2km，平均乘行距离=8.02km，取1.67m/s,取33km/h,国外研究建议步行到车站的概率分布符合高斯分布，概率主要分布在之内，故b取600m,s取30s，最大、最小站间距分别设为=650m、=2000m，编写C 程序，运行结果为：=26.2km、minT=1.156317h、d=1.64km；=18.3km、minT=1.0725h、d=1.66km。

由26.2/20=1.31＜1.64 及18.3/15=1.22＜1.66 可知地铁的平均站距小于小于模型求解的最优站距，但考虑到城市轨道交通以其运量大、快速、准时等特点，并且地铁是城市中适合中长距离运输的交通工具，因此其解答是较精确的。

2）1、2号线站点设置的合理性评价

由n=int(L/d)+1求出其站点总数=16考虑到轨道线路的始发站、终点站和换乘站（一般为地铁线路的交叉点）是必须设定的站点,所以由地图可以查得1、2号线一期工程与其他轨道线路的交点均为6，故1号线的最大站点数为22个，即(16 22)。

由已知条件可知=20（16 22），(11 17)我们不难发现是在满足乘客平均运行时间最小的情况下综合考虑了人流密度、方便换乘等约束条件确定出的站点的具体站点数，故1、2号线站点的设置合理。

3 郑州市地铁3、4、5、6号线路最优站点数确定

对的求解过程如下：

由已知条件可知=20、=15所以可以偏离其预测范围中值的偏差=（20-18）/18=11.11%，=(15-14)/14=7.14%所以平均中值偏差u=(+)/2=9.12%在误差的允许范围内。最优站点数取=int[.（1+u）]+1其计算结果如下表：

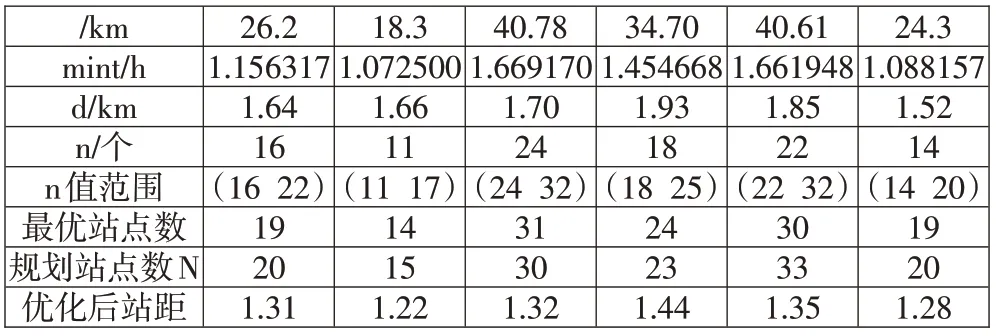
表1 预测结果及优化后结果

对比优化站点数与实际规划站点数N 可知：各点修正模型解与实际规划的站点数较为一致，因此该模对于实际生产具有一定的指导意义。

4 结论

本文采用轨道交通站间距优化对郑州市地铁1、2号线站间距的规划情况进行了评价，在此基础上对其余规划线路的站点设计进行优化。分析优化结果可知，郑州地铁站间距较为合理。但该模型也存在局限性，由于未考虑其他交通出行方式影响及具体的城市用地发展等社会自然因素，故在进行站点设置时应结合实际情况作进一步讨论。

[1]刘赛花，李金萍，呼超.轨道交通站间距优化模型的应用[J].黑龙江工程学院学报,2011，25（1）：36～39；

[2]魏金丽，梁平，阎岩，矫燕.城市轨道交通站点布局优化研究[J].青岛理工大学学报，2008，29（4）；

[3]徐浩，施超.城市轨道交通站点设置优化模型[J].中国科技信息，2006，（5）：119～120；

[4]覃裔.轨道交通枢纽规划与设计理论研究［D］.上海：同济大学，2002；