基于粗糙集和小波神经网络信息融合在加热炉控制中的应用
王 韬
(长春职业技术学院工程技术分院,吉林 长春 130033)
1 加热炉控制技术
1.1 加热炉控制技术概述
待轧钢坯根据计划被排列在加热炉内的滑轨上,用燃料和空气混合燃烧产生的热量进行加热,钢坯被加热到合适的温度后送给轧机进行轧制。燃料的燃烧需要适当配比的空气,空气量不足会造成燃料燃烧不充分从而浪费能源并污染大气;而空气过量时多余的空气会带走炉内热量,同时过量的空气会造成钢坯的氧化烧损,高效燃烧控制的重点就是空燃比的控制。考虑燃料和空气混合的实际情况,通常空气量要多于燃烧所需的理论值即理论空气量,空气过剩系数一般控制在1.05~1.10之间。
1.1.1 最佳燃烧控制
温度燃料空气流量串级调节在仪表控制系统中,处理燃料与空气的关系,通常采用配比调节,由于燃料与空气调节回路的响应速度不一致,流量测量孔板有误差,燃料的热值不稳定以及烧嘴特性等的变化,导致这种配比关系难以保证。特别是在燃烧负荷发生变化的情况下,更无法保持最佳配比。为解决这些问题,产生了3种处理空燃关系的交叉限幅法:单交叉限幅法、双交叉限幅法、改进型双交叉限幅法。
1.1.2 修正空燃比
在加热炉中各段内是否达到最佳燃烧效率,空燃比的设定是十分重要的,准确地调整空燃比对加热炉安全及产品质量也很重要。在常规的仪表控制系统中,空燃比往往由人工设定,但在频繁调节状态下,即使是最灵敏的传感器和调节阀也很难保证精确的空燃比。这是因为,流量测量孔板存在着误差,而且在燃料或空气的流速较低时,调节阀的位置及流速之间呈非线性关系。目前残氧闭环控制是修正空燃比的一种非常重要的方法。用氧化锆测定残氧量,用氧指示控制器调节输出修正空燃比,可以降低燃烧时的过剩空气量。由于加热炉各段互有影响,为此在各段都单设残氧量控制回路,并估算各段间的影响,采用多变量控制,通过计算求得加热炉各段残氧量调节回路的设定值,修正各段的空燃比。
1.1.3 附属回路调节及参数修正
在加热炉燃烧控制中,除了温度流量串级及残氧修正空燃比主要回路外,还有为减少路外冷空气侵入及火焰外喷的炉膛压力调节;保障流量调节回路稳定的燃气及空气总管压力调节以及为保证稳定的空燃比而进行的温度、压力及燃气的热值修正,这都是保证最佳燃烧所不可缺少的。通过集散控制系统进行这些修正是轻而易举的,且多采用PI控制或PID控制。
1.2 加热炉控制技术的工程应用现状
随着计算机控制系统、可编程控制器的出现和迅速发展,工业炉的计算机控制获得了日益广泛的应用,借助于现代控制理论的指导,向着过程和系统的优化控制方向迅速发展。从发展顺序和控制水平两个方面进行归纳总结,加热炉计算机控制大体上可以划分为如下3个层次:以提高燃料利用率、维持合理空燃比为目的,实现燃烧过程的自动控制(以炉温为控制对象);以优化钢坯加热过程自身为目标,实现炉温或者燃料消耗量的自动控制(以钢温为控制对象);在前后工序实现自动化的基础上,以协调优化整个生产系统为目标,实现加热工段的计算机自动化调度(以系统为控制对象)。
国际上,燃料控制已基本成熟,控制研究的重点已转移到以追求某种性能指标的优化控制方面,炉内加热过程的数学模型被广泛地应用在计算机控制上。近年来,随着连续加热炉自动控制系统的研究和实践,生产物料跟踪自动化水平迅速提高,标志着加热炉的控制已经进入自动控制的第三层次水平。
我国在这方面起步较晚,从20世纪80年代初才开始这方面的研究工作。但近10多年来,由于计算机技术以及智能控制技术的迅速发展,加热炉计算机控制的应用日趋广泛,控制水平有明显提高,并且取得了一些应用成果。
2 粗糙集理论描述
20世纪70年代初,波兰学者Z Pawlak和波兰科学院、华沙大学的逻辑家们组成了研究小组,开始了对信息系统逻辑特性的长期基础性研究。针对从实验中得到的以数据形式表述的不精确、不确定、不完整的信息和知识,进行了分类分析,这一研究成为粗糙集理论产生的基础。1982年Z Pawlak发表了经典论文Rough Sets[1],宣告了粗糙集理论的诞生。下面介绍粗糙集理论的基本概念及信息系统的属性。
2.1 不可分辨关系
不可分辨关系是粗糙集理论中的另一个重要概念。在决策表中,描述对象的属性是一种不精确信息,这种不精确信息造成了对象之间是不可分辨的或不分明的,观察这种不可分辨关系的对象正是粗糙集理论研究的出发点。
S为知识表达系统,令P⊆A,定义属性集P的不可区分关系IND(P)为
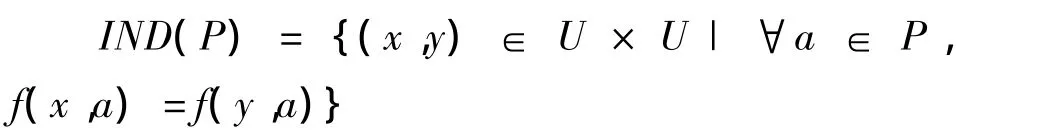
若(x,y)∈IND(P),则称x和y是P不可区分的。
不可分辨关系实际上是一种等价关系,具有不可分辨关系的对象是属性值完全相同的对象。符号U|P表示不可区分关系IND(P)在U上导出的划分。IND(P)中的等价类称为P基本集。
2.2 知识表达系统和决策表
在粗糙集理论中,知识表达系统S是一个四元组:
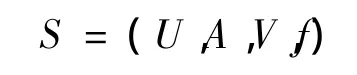
式中:U为对象的非空有限集合,称为论域;A为属性的非空有限集合;为属性 a值域;f为U×A→V,是一个信息函数,为每个对象的每个属性指定一个属性值。
设 S=(U,A,V,f),A=C∪D,C∩D= Ø。C和D分别称为条件属性集和决策属性集,具有条件属性和决策属性的知识表达系统称为决策表。
2.3 属性约简与核
定义:设U为一个论域,P和Q为定义在U上的两个等价关系族且Q≤P,如果。
(1)IND(Q)=IND(P)
(2)Q是独立的
则称Q是P的一个绝对约简。
定义:设U为一个论域,P为定义在U上的一个等价关系族,P中所有绝对必要关系组成的集合称为关系族P的绝对核,记作CORE(P)。
2.4 边界域与粗糙度
给定知识表达系统S=(U,A,V,f),对于每个子集X⊆U和不分明关系R,可以根据R的基本集合描述来划分集合X:
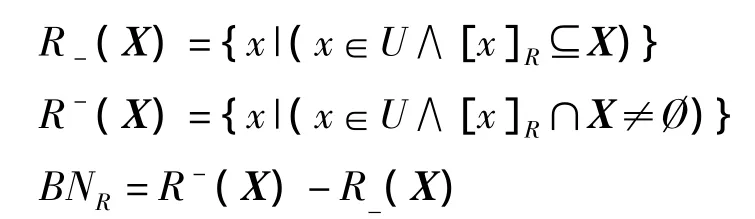
式中:R-(X)和R-(X)分别称为X的R下近似集和上近似集;BNR(X)称为X的边界域。显然,当BNR(X)≠0时,X为粗糙集。
假定集合X是论域U上的一个关于知识R的Rough集,定义其R,Rough集为:
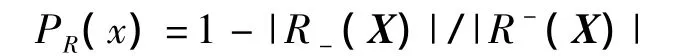
式中|·|表示集合元素数,且X≠Ø
3 遗传小波神经网络
小波神经网络是基于小波分析而构成的神经网络模型,即用非线性小波基取代通常的Sigmoid函数,图1所示网络与径向基函数神经网络相类似,对称子波通过伸缩参数构成了一径向基函数族。其信号表述是通过将所选取的小波基进行线性叠加而实现,其网络拓扑结构如下:
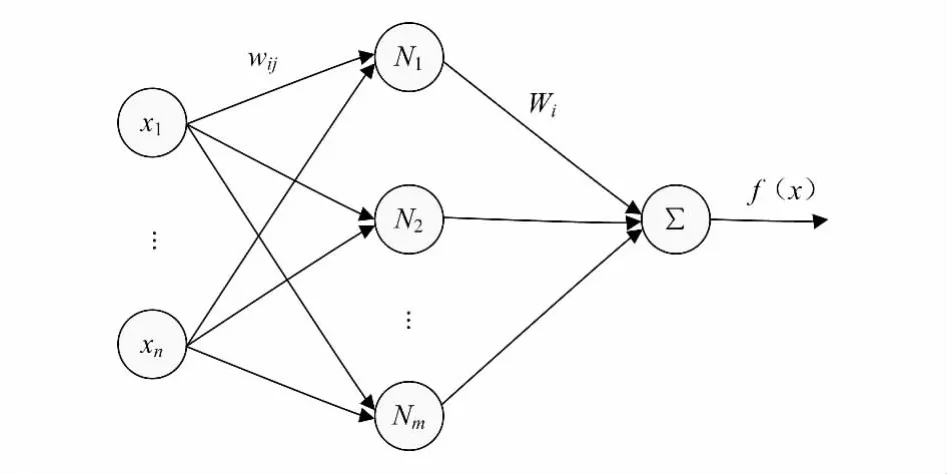
图1 小波神经网络拓扑结构
网络输入为 [x1,x2,…,xn],输出可表示如下:
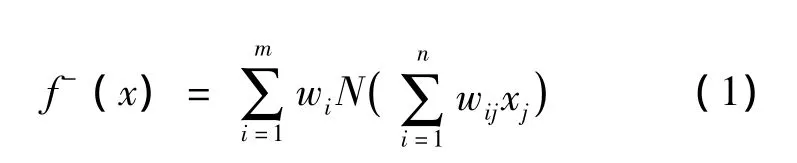
式中:wi为隐层与输出层的连接权值;wij为输入层与隐层的连接权值,即输入层的第j单元与隐层第i单元的连接权值;m为隐层节点个数。
网络参数wi,wij可以通过求一能量函数的极小值而优化得到:
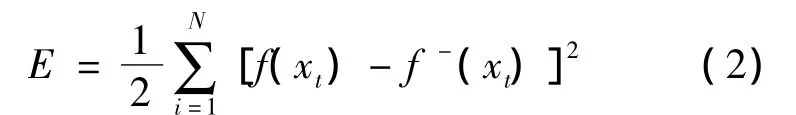
式中:xt表示第t组训练样本;f(xt)表示第t组训练样本作为输入所对应的期望输出;f-(xt)表示第t组训练样本作为输入所对应的实际输出。
4 粗糙集和遗传小波神经网络的结合
粗糙集和遗传小波神经网络结合的具体步骤如下:
第一步,分析数据,选取原始样本集,形成原始决策表。
第二步,对原始决策表进行连续数据的离散化。
第三步,利用粗糙集方法,对离散化后的决策表进行约简,形成最终决策表。
约简步骤为:(1)在决策表中,合并相同的规则,即消去相同的行;(2)根据知识简化的方法进行条件属性的简化,即从决策表中消去某一列;(3)查看规则的相容性来确定条件属性的冗余性,并消去冗余属性;(4)根据范畴的简化方法,消去每一决策规则中的属性冗余值;(5)获取最小决策表。
第四步,根据系统的要求以及传感器的特点选择合适的小波网络模型,对建立的神经网络系统进行离线学习,确定网络的联接权阈值。
第五步,用检验数据对已训练好的网络进行检验。
第六步,结果的统计分析。
5 基于粗糙集和遗传小波神经网络信息融合的加热炉控制
5.1 遗传小波神经网络多传感器信息融合系统结构
遗传小波神经网络多传感器信息融合系统结构如图2所示,系统由测量传感器、预处理和融合小波神经网络组成[2]。
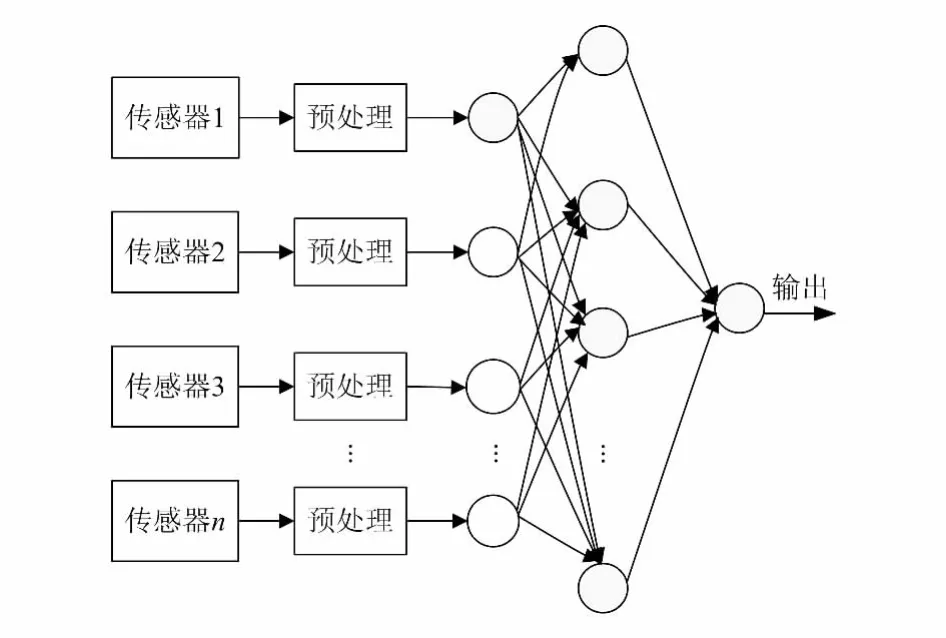
图2 遗传小波神经网络多传感器信息融合系统结构图
5.2 聚合控制
聚类融合控制(如图3所示)不是像常规的控
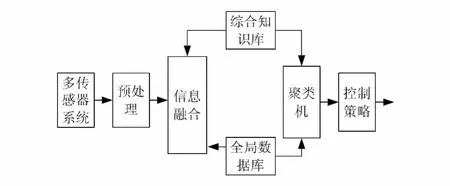
图3 聚类融合控制
制那样直接利用传感器的检测数据进行操作控制,而是融合传感器数据将生产过程的状态分成有限的类别,根据每一类别所描述的过程行为特点进行相应的操作控制。
从理论范畴看,聚类融合控制的理论基础是聚类分析和信息融合,同时要应用模式识别、神经网络以及专家系统等方面的理论。所以,聚类融合控制可以看成是上述多个领域的结合和交叉。它需要综合应用上面几个领域的基本概念和方法,并结合实际工业对象的领域知识,完成监测控制系统的设计和实施。
6 粗糙集和遗传小波神经网络的仿真
控制策略空间U由类别空间B经映射Ψ而构成,而且通常要用到输入信息X、全局数据库D和综合知识库K的有关知识。在本系统中,参与输出控制的输入信息有:

按聚类融合控制的思想,系统在运行空间B中的位置(加热段工况)及出口钢坯温度T0决定控制输出Δn,如图4所示。图中纵坐标为加热段工况,横坐标为出口钢坯温度与期望值之差ΔT0=T*0-T0。ΔT0的类别划分越细,控制效果就越好,但是控制复杂性也相应增加。
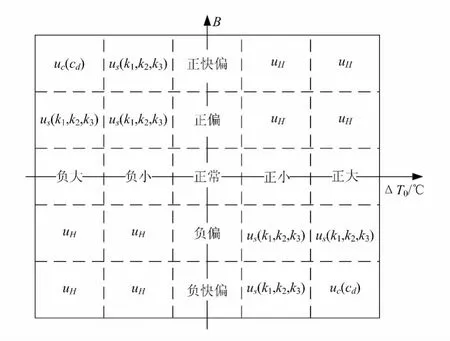
图4 聚类融合控制策略空间
聚类融合控制的输出为流量控制阀控制值n:
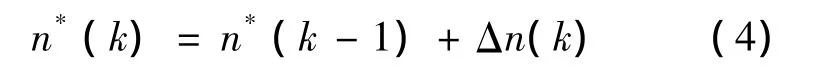
式中:k为控制的拍数;Δn(k)为流量调节增量值[3]。
加热炉出口钢坯温度的期望值在1350℃左右,实际钢坯温度范围在1200℃ ~1500℃。所以ΔT0的最小值为1200-1350=-150℃,最大值为1500-1350=150℃,因此可以得到煤气流量控制阀的策略空间,如图5所示。
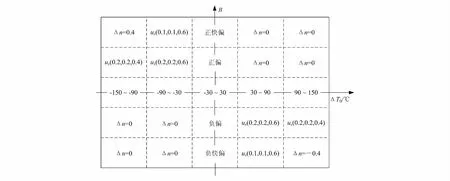
图5 加热炉融合控制策略空间
以9000s的温度采样数据为例,采用粗糙集和遗传小波神经网络控制理论得到的加热炉流量控制阀开度变化仿真曲线如图6所示[4]。
由加热炉对象模型可知,当以控制阀n作为输入量,钢坯温度作为输出量时,采用基于神经网络融合控制理论的钢坯温度仿真曲线如图7所示。
基于神经网络融合控制能适时调节煤气流量控制阀,从而使加热炉加热段出口钢坯温度保持在设定值附近,波动不超过±5%,达到了较为满意的效果。
7 结束语
小波神经网络作为基于小波分析的新的神经网络,凭借小波分析在信号时频域分析方面的特点成为科学技术界在工具和方法上的重大突破,极大地推进了神经网络在理论研究和工程应用领域新发展。本文从加热炉应用出发给出的一种多传感器信息融合的结构,就较好地克服了以往神经网的络结构设计的盲目性。
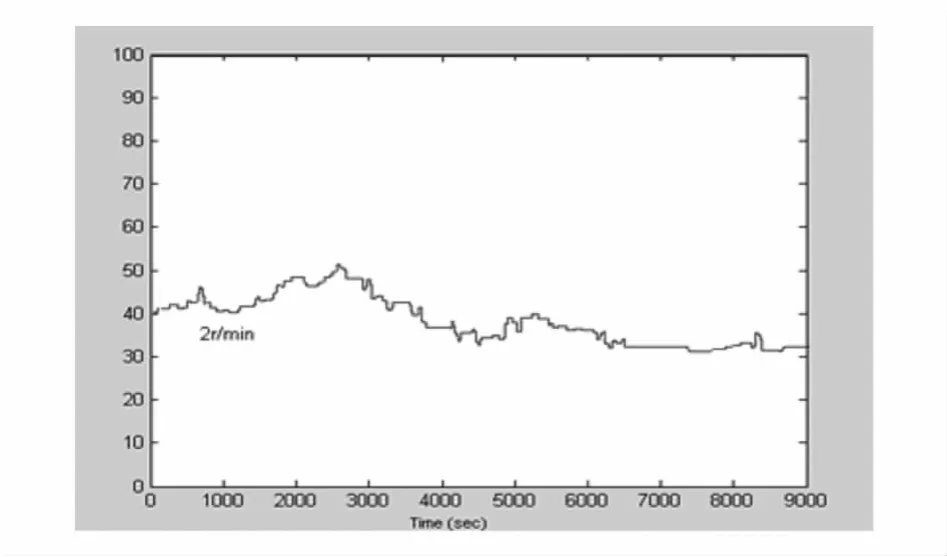
图6 采用聚类融合控制控制阀运行的仿真曲线
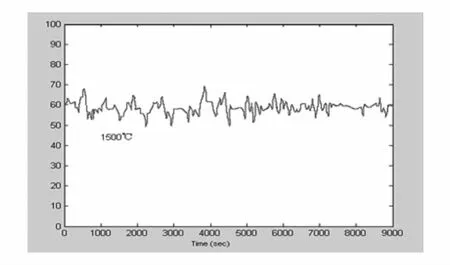
图7 采用聚类融合控制温度的仿真曲线
[1] 王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社,2001.
[2] 何友,王国宏.多传感器信息融合及应用[M].北京:电子工业出版社,2000:39-41.
[3] 杨自厚.神经网络技术及其在钢铁工业中的应用[J].冶金自动化,1996,20(4):52-55.
[4] 丛爽,郑毅松,王怡雯.ART-2神经网络的改进及建模实现[J].计算机工程与应用,2002,38(14):25-27.

