悬臂柔性围护桩所受土压力的反算

蔡 晖

(福建省高速公路建设总指挥部，福建福州 350000)

1 土压力计算方法

目前关于基坑围护结构所受土压力的计算方法很多，然而由于各土压力算法基本假设的局限性，大部分土压力计算理论都存在各自不足之处。悬臂围护开挖的基坑，其基坑深度一般不大，受力简单，因此对于弹性桩的情况，可以根据围护桩的挠曲变形来反算围护桩所受土压力，亦可以先根据围护桩的变形，反算出桩前土抗力大小，再利用静力平衡原理反算出桩后土压力[1，2]。

1.1 根据桩身挠曲变形反算的土压力

嵌固深度h＞2.5/a时的围护桩可视为弹性桩，此时围护桩在土压力作用下只发生挠曲变形[3]。由于悬臂围护桩的受力比较简单，因此，理论上可以根据桩的侧向变形拟合出挠曲方程，并利用围护桩挠度方程的物理意义反算出土压力的分布情况。根据《基坑围护技术规程》中的土压力分布，围护桩所受土压力分布如图1所示。

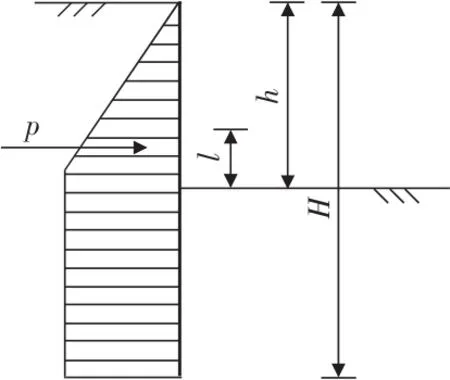
图1 围护桩所受土压力分布图

则可以得到开挖面以上距开挖面l高度处围护桩的弯矩方程为:

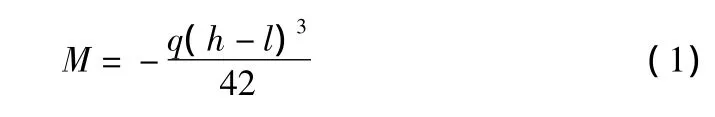
其中，h为开挖深度;l为距开挖面的距离。再根据围护桩挠度方程的物理意义可得到:

其中，E为桩身材料的弹性模量，对于C30钢筋混凝土，E=31 GPa;I为桩的截面惯性矩，对于圆形桩

联立式(1)，式(2)并积分可以得出桩的挠度方程:

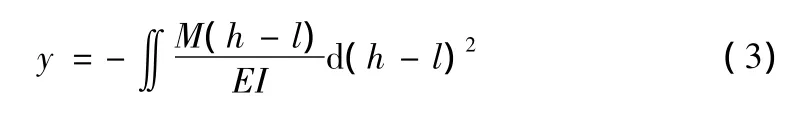
其挠度方程的系数与开挖深度l相关，因此，可以根据现场实测的数据，对该挠度方程进行拟合即可反算出围护桩背后所受土压力的大小。

1.2 根据静力平衡反算的土压力

先对围护桩的现场实测位移进行拟合，即可确定围护桩的位移曲线方程y(x)，再结合弹性地基梁的基本原理，可以得出围护桩桩前所受土抗力分布情况及大小，由于围护桩处于悬臂状态，并没有受到内围撑的轴力，假设桩后土压力如图1所示中分布，则可以根据弹性地基梁所计算出来的桩前土抗力结合静力平衡即可反算出桩后所受土压力的大小[4]。

桩前土抗力:

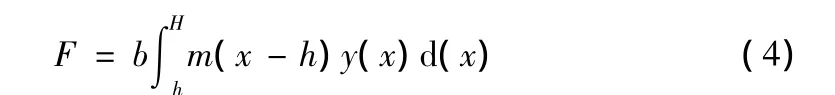
其中，x为距桩顶深度;b为计算宽度，圆形桩为b=0.9(1.5d+0.5);h为基坑开挖深度;H为围护桩桩长;m为土抗力系数。根据桩身受力的平衡方程计算桩后所受土压力合力:

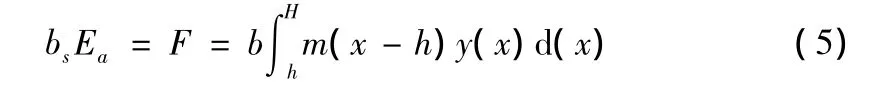
其中，bs为围护桩间距;根据围护桩所受土压力分布及合力即可反算出围护桩桩后开挖面h处所受土压力大小p(h):

2 土压力的反算

以双流机场隧道基坑DK173+850～DK173+960段典型断面DK173+875，DK173+955为研究对象，对以上两种悬臂开挖下围护桩土压力反算方法及经典的土压力方法计算结果进行对比分析。

2.1 计算断面概况

成绵乐客运专线双流机场隧道DK173+850～DK173+960断面上部采用放坡开挖(坡高1.0 m～4.2 m，坡率1∶1)，下部施作围护结构后进行直立开挖。围护结构主要采用悬臂式围护桩，围护桩为钢筋混凝土灌注桩，桩径1.2 m，桩距2.4 m，桩长17.7 m，嵌固深度4.03 m～5.18 m，桩身混凝土强度等级为C30;其断面结构如图2所示，土层的物理力学参数及层厚见表1。

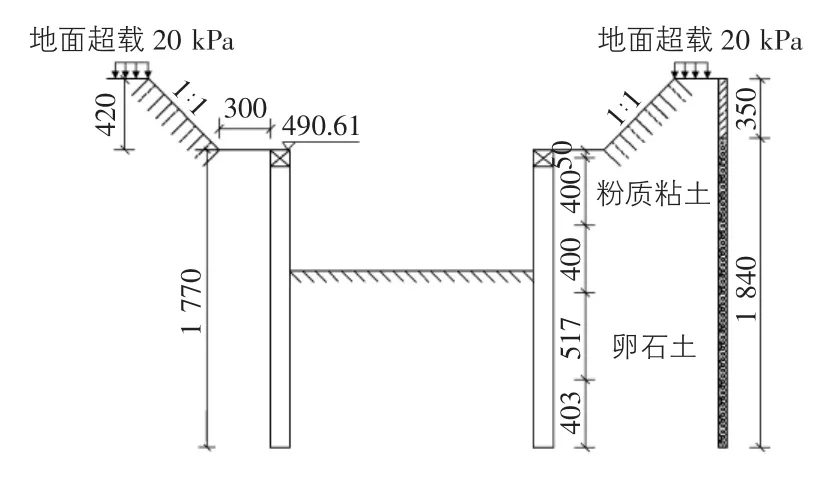
图2 DK173+850～DK173+960断面结构示意图

表1 土层的物理力学参数及层厚

其中DK173+875，DK173+955断面上部分采用悬臂开挖，其开挖深度为7 m，经验算为柔性桩，因此，根据文中1节的方法对其土压力进行反算。

2.2 根据围护桩的挠曲方程反算土压力

根据式(1)，式(3)当基坑开挖为7 m时，DK173+875，DK173+955断面围护桩挠曲方程为:

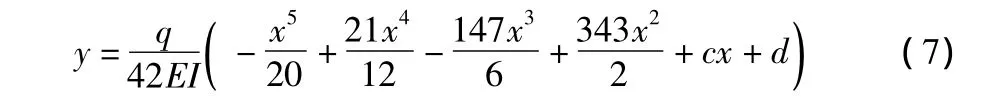
根据式(7)可得DK173+875，DK173+955断面围护桩在土压力作用下变形的挠度方程(注:挠度方程的拟合必须符合该系数比例，否则该方程只具有几何意义而失去其挠度方程的物理意义)，如图3所示。

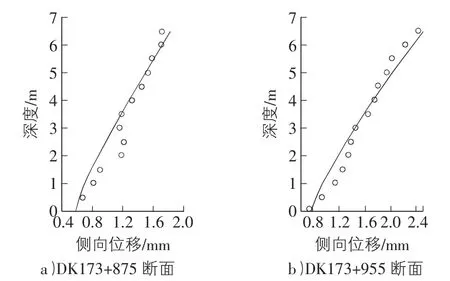
图3 围护桩挠度方程拟合曲线

其中DK173+875围护桩变形挠度方程:

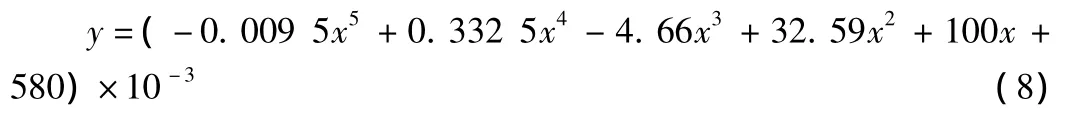
其中DK173+955围护桩变形挠度方程:

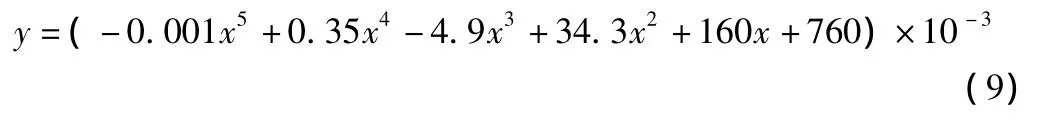
根据围护桩挠度方程的物理意义及式(8)可以得到:

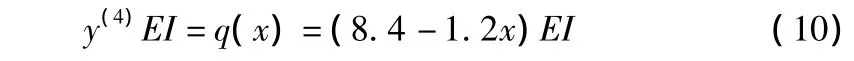
其中，混凝土强度等级为C30的弹性模量，E=31 GPa，因此，根据式(10)当x=0时DK173+875断面围护桩7 m处所受土压力:p=10.29 kPa，同理根据式(9)可得，DK173+955断面围护桩7 m处所受土压力:p=10.83 kPa。

2.3 根据静力平衡反算土压力

将现场所得数据按多项式进行拟合可以得到围护桩侧向位移曲线方程y(x)(注:该方程只需具备几何意义)，如图4所示。

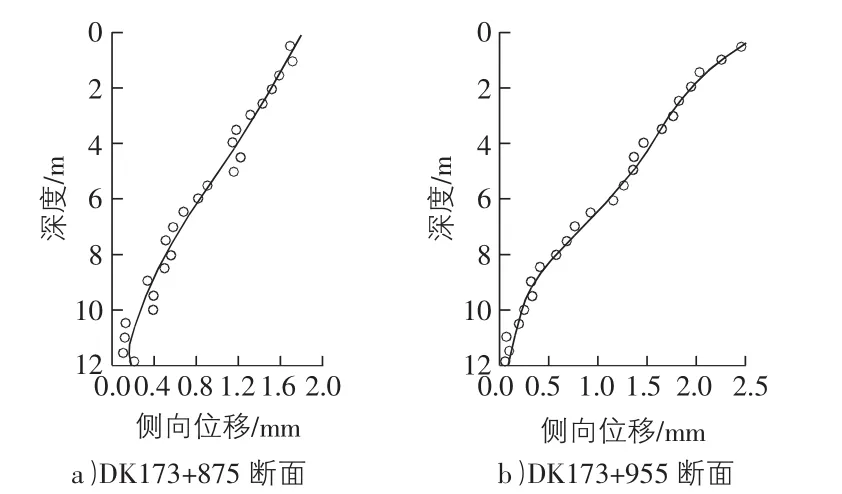
图4 围护桩侧向位移曲线

其拟合多项式为:

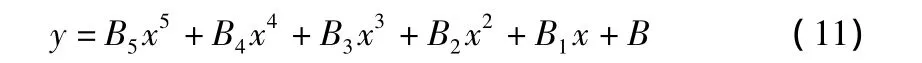
其系数见表2。

表2 多项式系数

根据式(11)及表2可得卵石土m=36 MN/m4，围护桩为圆形桩，桩径d=1.2m，因此，桩前弹簧计算宽度b=2.07 m。

再根据式(4)，式(5)可得:DK173+875断面围护桩桩后土压力合力F=406.37 kN，DK173+955断面围护桩桩后土压力合力F=530.6 kN。

由式(6)可得:DK173+875断面围护桩7 m处土压力p=12.54 kPa，DK173+955 断面围护桩7 m 处土压力 p=16.37 kPa。

3 计算结果的合理性分析

本文2节中计算出了DK173+875断面、DK173+955断面围护桩悬臂开挖7 m时，根据挠曲方程及静力平衡反算的围护桩所受土压力大小及分布，本节将利用madis有限元软件对2节所得土压力进行验算，并将其与郎肯主动土压力理论计算结果及实测数据进行对比分析，对其准确性进行验证。

3.1 模型建立

利用madis有限元软件进行建模计算，计算方法采用弹性地基梁法，其中弹性地基梁杆系有限元法的一般分析过程为:结构理想化→结构离散化→形成单元刚度矩阵→单元刚度矩阵集成总刚度矩阵→利用平衡方程求解得到节点位移[5-7]。计算简图如图5所示。

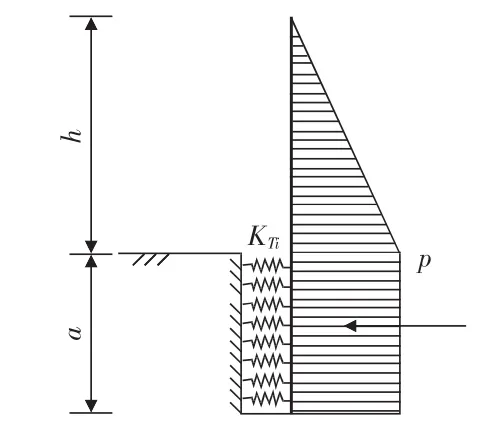
图5 计算简图

在计算模型中，围护桩桩后土压力以外荷载的形式施加于围护桩上，桩前土体则按弹性地基梁的原理根据m法把土体假设为土弹簧，其中开挖面以下a深度处桩前土弹簧的计算刚度采用式(12)计算所得:KTi=smZb (12)

其中，s为土弹簧间距;m为土抗力系数;Z为距开挖面以下深度。在本文中，土弹簧间距s=0.5 m，围护桩为圆形桩，桩径d=1.2 m，计算宽度b=2.07 m，卵石土土抗力系数根据经验公式计算得m=36 MN/m4。各工况下围护桩变形计算采用“全量法”，即相应的土压力全部作用在围护结构上。

3.2 模型计算

通过计算可以得到DK173+875断面围护桩在郎肯主动土压力、根据挠度方程反算的土压力及根据静力平衡反算的土压力作用下所得的围护桩位移，如图6所示。

其中:图6a)为按挠度方程反算的土压力、图6b)为按静力平衡反算的土压力、图6c)为按郎肯主动土压力计算结果。

采用同样的方法可以得到DK173+955断面计算结果。

3.3 位移计算结果及对比分析

根据计算所得的桩身侧向位移见表3。

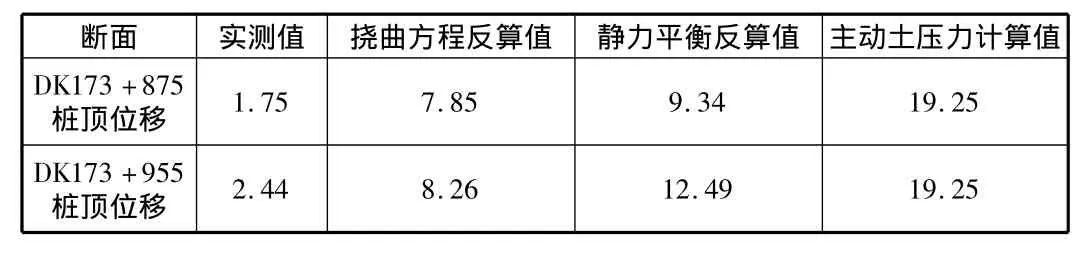
表3 计算桩顶位移 mm

由表3可以得出:

1)根据围护桩桩顶位移分析:DK173+875断面围护桩、DK173+955断面围护桩采用郎肯主动土压力计算所得桩顶位移与实测值相差较大，按挠度方程及静力平衡反算所得土压力计算其结果与实测值更加接近。2)根据围护桩变形形态分析:由图7 DK173+875断面围护桩及DK173+955断面围护桩变形可知，各土压力计算所得围护桩变形形态与实测值基本相同，因此，以上各算法的土压力分布与围护桩实际所受的土压力的分布情况基本吻合。

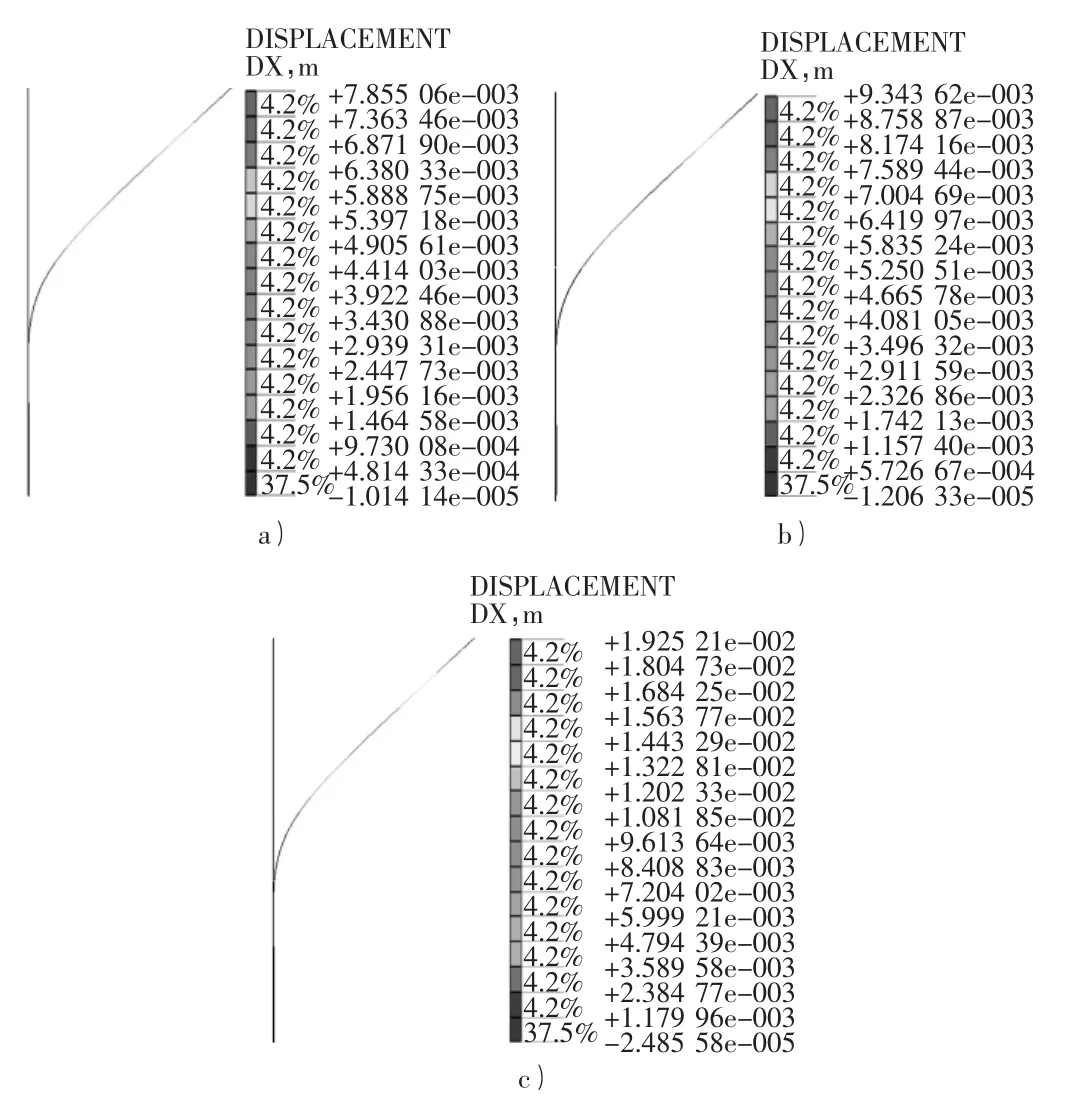
图6 DK173+875断面围护桩计算结果

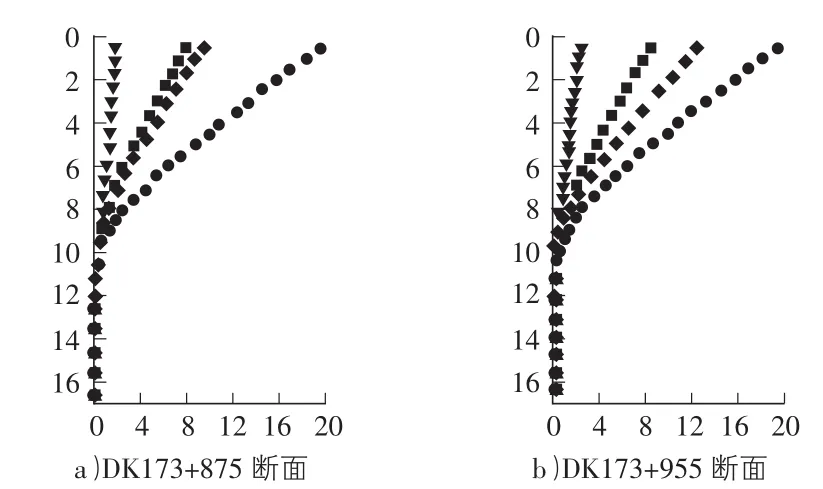
图7 围护桩侧向位移计算结果

4 结语

本章依托双流机场隧道基坑围护桩现场实测数据，根据围护桩挠曲方程及静力平衡法，对悬臂开挖条件下围护桩所受土压力进行了反算，并对其合理性进行了分析，所得结论如下:

1)对于开挖深度较小的悬臂开挖情况，将郎肯主动土压力作为围护桩所受荷载，采用弹性地基梁法，通过madis有限元软件计算所得的桩身侧向位移与实测值相差较大。2)对于开挖深度较小的悬臂开挖情况，当围护桩嵌固深度h＞2.5/a即围护桩为弹性桩时，采用本文提出的根据围护桩挠曲方程及静力平衡法反算所得的土压力作为围护桩所受荷载更加合理。

[1] 冶金工业部建筑研究院.建筑基坑工程技术规范[M].北京:冶金工业出版社，1998:104-120.

[2] 许锡昌，陈善雄，徐海滨.悬臂排桩支护结构空间变形分析[J].岩土力学，2006，27(2):184-188.

[3] 陈祖煜，迟 鸣，孙 平，等.计算柔性支挡结构主动土压力的简化方法[J].岩土工程学报，2010，32(1):22-27.

[4] 宋建学，翟永亮，莫 莉.基于支撑内力和支护桩位移实测量的 m 值反算[J].岩土工程学报，2010，32(1):156-157.

[5] 李 明.基坑悬臂支护结构的土压力数值研究[D].南京:河海大学硕士论文，2003.

[6] 赵 宝.悬臂桩基坑支护影响因素分析及研究[D].西安:长安大学硕士论文，2010.

[7] 张强勇.弹性地基梁杆系有限元法在深大基坑工程支护设计中的应用[J].建筑结构学报，2005，26(3):114-117.