HTI介质饱和流体特性和裂缝密度对方位反射系数的影响

李春鹏，印兴耀，张 峰

（1.中国石油大学（华东）地球科学与技术学院，山东青岛 266580；2.中国石油大学（北京）地球科学学院，北京 102249）

HTI裂缝介质是指一组近垂直定向排列的裂缝地层，表现为方位各向异性，即反射系数随着观测方位的变化而变化。方位反射系数与裂缝密度和充填流体性质等有关，因此可以通过地震岩石物理方法建立HTI介质弹性矩阵，根据弹性矩阵和地震波传播特征构建HTI介质弹性波反射／透射方程，据此可以研究裂缝参数与方位反射系数之间的关系。Brown等［1］推导出各向异性岩石骨架有效弹性模量与该骨架充填流体时的有效模量之间的理论关系式，但是该理论要求所有岩石矿物组成具有相同的体积模量和剪切模量。Cheng（1978，1993）［2－3］给出了TI介质有缝岩石的等效模量模型。Hudson（1980，1981）［4－5］给出了TI介质弹性矩阵的构建方法，但由于假设裂缝之间互不连通，该方法仅适用于高频情况下的弹性矩阵构建。Thomsen（1995）［6］认为裂缝型岩石由各向异性裂缝和均匀各向同性含粒间孔隙的背景介质组成，流体可以通过孔隙在裂缝之间流通，据此提出了低频和中高频两种情况下的弹性矩阵构建方法。该方法更适用于计算地震尺度下HTI裂缝介质弹性矩阵。但由于Thomsen裂缝理论要求背景介质纵、横波速度和岩石基质模量是已知的，而测井声波时差和横波时差受到裂缝和各向异性的影响，只代表某一方向的裂缝型岩石综合慢度，因此，对于饱和流体岩石背景介质弹性模量的计算主要是采用Hill平均理论［7－9］和Kuster－Toksoz理论［10］。

精确的HTI介质弹性波方位反射特征需要通过求解反射／透射方程得到，虽然Ruger（1996）［11］和Vavrycuk等（1998）［12］分别独立地推导了HTI介质方位AVO 线性近似公式，但是他们并没有给出HTI介质弹性波精确反射／透射方程。国内许多学者对于方位AVO 反射特征的研究也是基于近似公式进行的［13－14］。梁锴（2009）［15］提 出TTI介质二维反射系数公式，可是该公式不适用于三维情况下的反射系数计算。根据HTI介质弹性矩阵和波动方程，推导HTI介质Christoffel方程，研究出HTI介质相速度和偏振方向，再结合弹性介质边界条件推导HTI介质弹性波反射透射方程，可以进行HTI介质精确方位反射特征研究。

我们将等效介质理论和Thomsen裂缝理论相结合，计算了HTI裂缝介质的弹性矩阵，并推导出HTI介质弹性波三维反射／透射方程；然后应用该方程计算方位反射系数，研究了裂缝流体类型和裂缝密度与方位反射系数的关系。

1 HTI裂缝介质弹性矩阵构建

Thomsen［6］1995年提出构建饱和流 体HTI裂缝介质弹性矩阵的方法，该方法假设岩石背景介质是均匀各向同性含粒间孔隙的，背景介质嵌入裂缝后的复合介质是对称轴垂直于裂缝面的横向各向同性介质。同时，Thomsen假定背景介质纵、横波速度和岩石基质模量已知并利用Gassmann理论［16］计算背景介质骨架和饱和流体情况的弹性模量。由于测井声波时差和横波时差受到裂缝和各向异性的影响，只代表某一方向的裂缝型岩石综合慢度，因此需要结合等效介质理论计算背景介质的纵、横波速度。通过测井方法可以获得地下岩石矿物成分，结合Hill理论公式

可以计算岩石基质模量。式中：Ki，μi，ρi和fi分别表示第i种固体颗粒的体积模量、剪切模量、密度和体积百分数，一般可以通过测井曲线计算获得；n是矿物种类；KV和μV分别表示用等应变平均计算出的岩石基质体积模量和剪切模量；KR和μR分别表示用等应力平均计算出的岩石基质体积模量和剪切模量；Km和μm 分别表示用Hill理论计算出的岩石基质体积模量和剪切模量；ρm 表示岩石基质密度。

背景介质骨架由岩石基质和岩石孔隙组成，根据Thomsen理论，背景介质孔隙流体在低频情况下可以相互流动，因此可以先利用Kuster－Toksoz理论和岩石基质等效模量计算背景介质骨架等效模量，再应用低频Gassmann理论向背景介质孔隙中加入流体，得到饱和流体背景介质弹性模量［11］。根据Kuster－Toksoz理论，假设岩石孔隙是球体状的，则可以根据公式

得到背景介质骨架弹性参数。式中：K＊和μ＊分别表示背景介质骨架体积模量和剪切模量；φp是背景介质的孔隙度；ζm 是Kuster－Toksoz理论系数；E＊和σ＊分别是背景介质骨架的杨氏模量与泊松比。根据Gassmann流体理论，即

可以确定饱和流体岩石弹性参数。式中：K和μ分别表示背景介质饱和流体时的体积模量和剪切模量；Kf表示流体体积模量；E和σ分别是背景介质饱和流体时的杨氏模量与泊松比。

结合背景介质弹性参数和Thomsen 裂缝理论，可以得到HTI介质弱各向异性参数，即

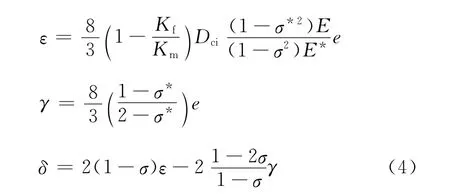
其中ε，γ，δ分别表示Thomsen弱各向异性参数；e代表裂缝密度，它可以写成单位体积裂缝数目Nv和平均立方直径a的形式，即e＝Nv（a3／8），或者可以写成裂缝孔隙度φc 和纵横比c／a的形式，即是裂缝厚度；Dci是流体的影响因素，低频情况下

中高频情况下

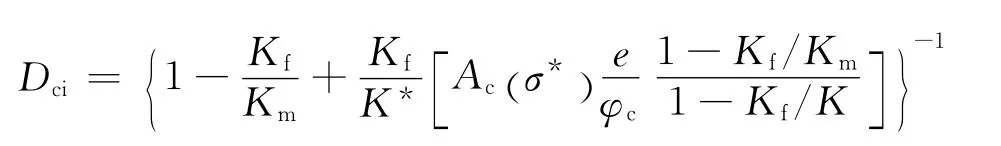
各向同性背景介质（不含裂缝）的纵、横波速度可以表示为

式中：vp0，vs0分别表示背景介质不含有裂缝时的纵、横波速度；ρ，vp90和vs‖90分别是背景介质含有裂缝时的密度和各向同性面的纵、横波速度。根据（5）式求得vp90和vs‖90，可以得到HTI介质弹性矩阵

其中，

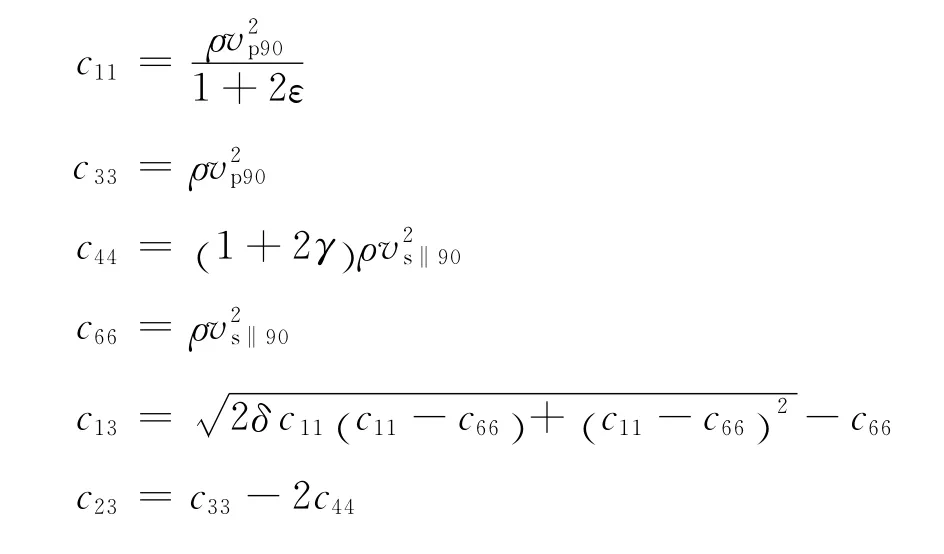
2 HTI介质弹性波反射／透射方程推导

各向异性介质弹性波控制方程是各向异性弹性波的波动方程和Christoffel方程，是研究地震各向异性的理论基础和研究地震波传播规律的根本出发点。Christoffel方程是由波动方程导出的，用以研究地震波的相速度和偏振方向等传播特征。通过广义Snell定律可以推导出HTI介质反射角／透射角公式，结合相速度和偏振方向得到HTI介质地震波传播函数，并根据边界条件推导出HTI介质弹性波三维反射／透射方程。

2.1 HTI介质相速度

梁锴（2009）［15］曾根据弹性波波动方程推导各向异性Christoffel方程，同理可将HTI介质弹性矩阵代入波动方程得到HTI介质Christoffel方程。令该Christoffel方程的系数行列式为0，得到HTI介质相速度公式

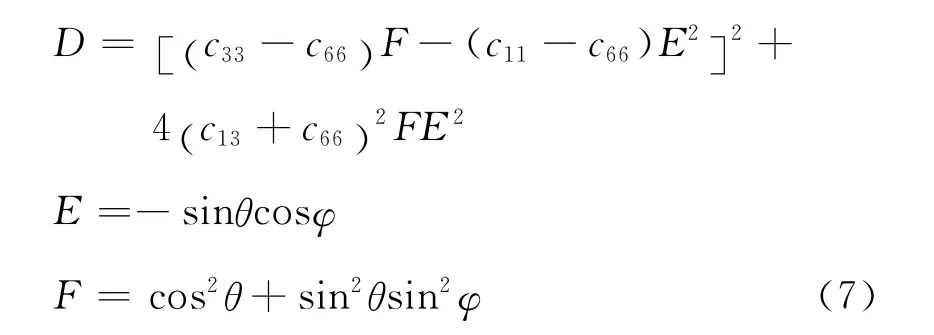
式中：vP表示qP波相速度；vSV表示qSV波相速度；vSH表示SH 波相速度；θ是入射角；φ是方位角，表示为地面观测线相对于对称轴的顺时针夹角。

2.2 HTI介质地震波偏振方向

将相速度公式代入HTI介质Christoffel方程，可得HTI介质偏振向量，即

式中：PSH是SH波偏振向量；PqP是qP波偏振向量；PqSV是qSV 波偏振向量；c是任意非零实数。定义Px，Py，Pz分别是偏振向量在x，y，z方向的分量；α表示相速度与z轴的夹角；β表示相速度在x－y面的投影与x轴的夹角。为了方便研究，假设Px为正，通过调节c的大小控制Px符号。

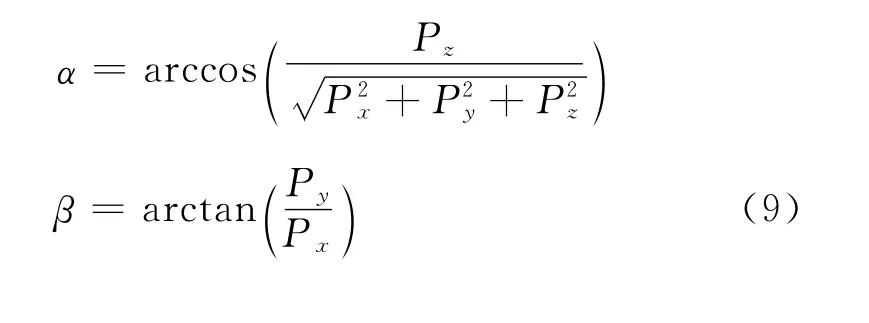
如果Px和Py都为0，那么偏振方向与z轴一致，即α＝0，β＝π／2。

2.3 反射角和透射角公式

假设θip1，θp1，θsv1，θsh1，θp2，θsv2，θsh2分别为入射qP波、反射qP 波、反射qSV 波、反射qSH 波、透射qP波、透射qSV 波、透射qSH 波的波前面法向与z轴的夹角，下标“1”和“2”分别表示上覆HTI介质和下伏HTI介质。由广义Snell定律得

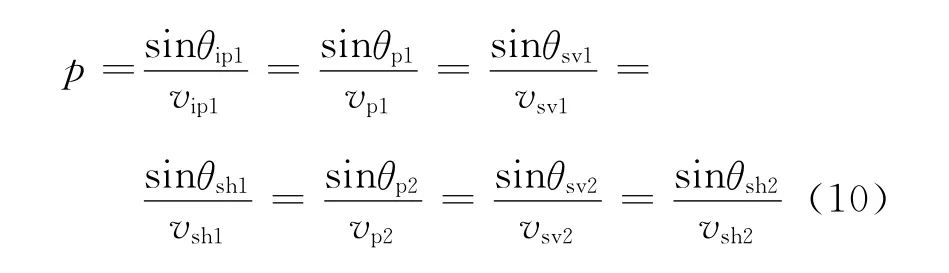
将（7）式表示的相速度公式代入上式解得

1）θp1和θp2满足

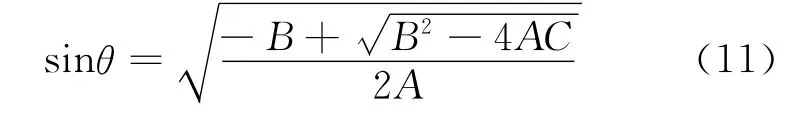
2）θsv1和θsv2满足

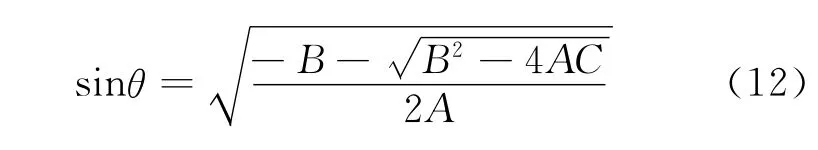
3）θsh1和θsh2满足

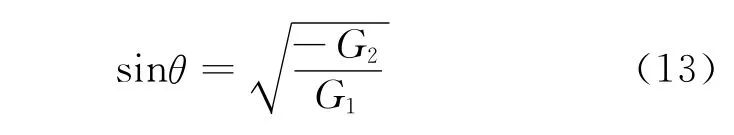
其中，A，B，C，G1，G2中涉及到的cij表示相应地震波传播介质的弹性参数。

2.4 HTI介质弹性波反射／透射方程推导

假设U1，U2，U3，U4，U5，U6，U7分别表示入射qP波、反射qP波、反射qSV 波、反射SH 波、透射qP波、透射qSV 波、透射SH 波的波函数；A是初始振幅；RPP，RPSV，RPSH分别表示qP波、qSV波、SH波反射系数；TPP，TPS，TPSH分别表示qP波、qSV波、SH波透射系数。再假设上、下介质裂缝对称轴方向一致，选择位移函数为基本求解函数，在观测系统坐标系下分别写出如下波函数。

根据弹性理论，这7个波函数在弹性界面上应满足位移连续条件和应力连续条件，即

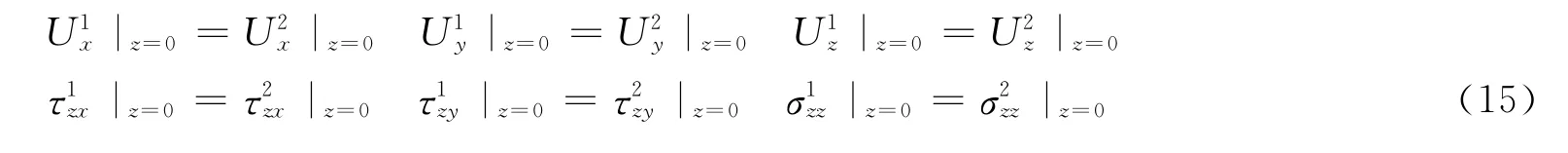
其中，上标“1”表示上覆HTI介质的标志，上标“2”表示下伏HTI介质。对于位移连续函数，当z＝0时有

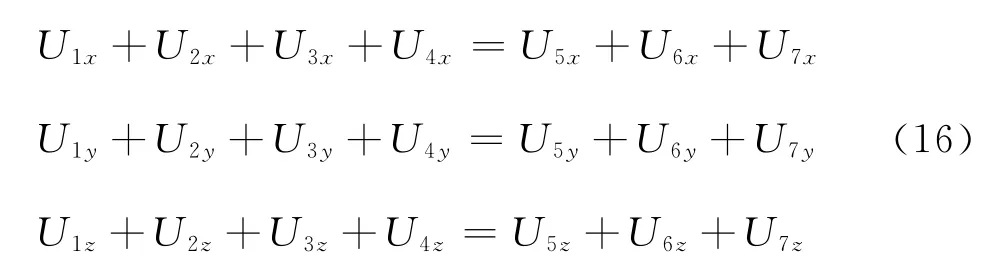
把波函数代入上式得到上、下HTI介质对称轴一致的弹性波反射／透射方程：

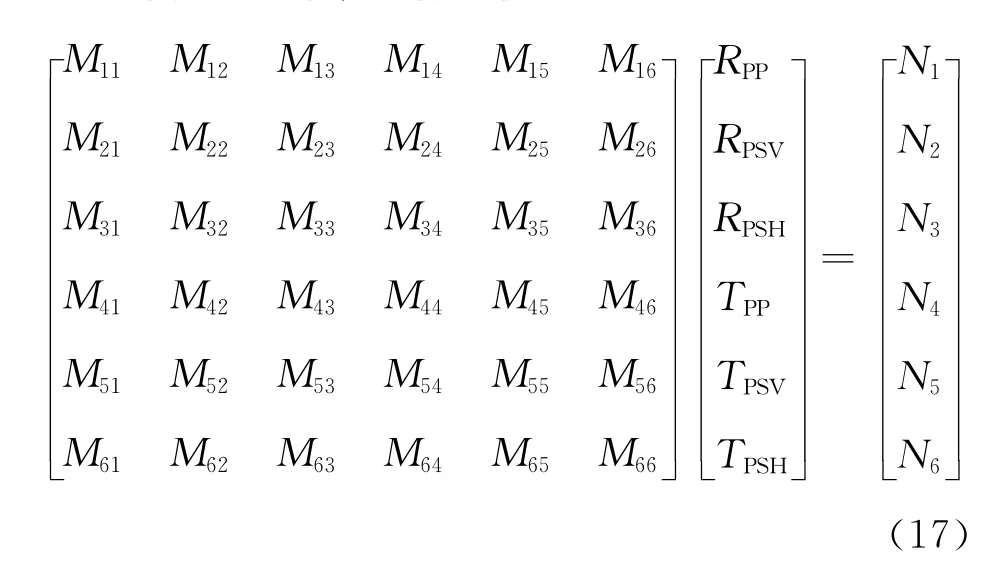
其中

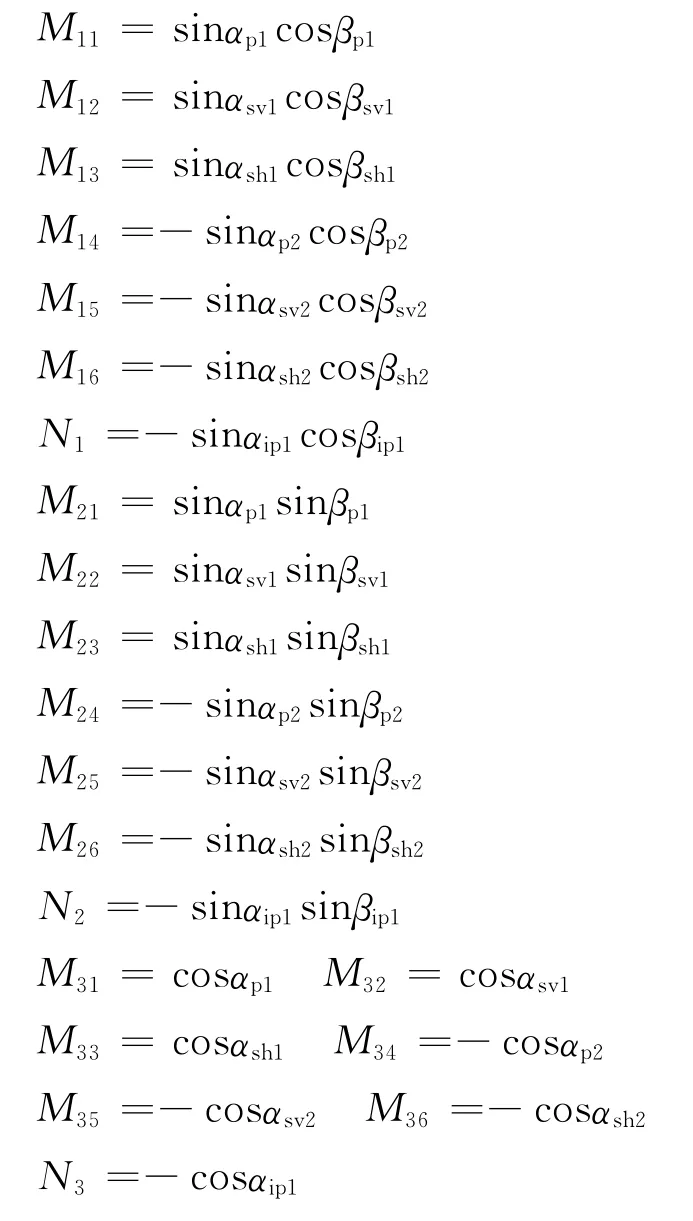
3 模型试算

3.1 地震波在HTI介质中的传播特征

模型分析主要采用双层介质模型，且假设上覆介质为各向同性墨西哥湾黏土，下伏HTI介质为嵌入近垂直定向分布裂缝的饱含水黏土砂岩，裂缝密度和裂缝纵横比分别为0.1 和0.001（表1 和表2）。图1a显示了基于HTI介质弹性波反射／透射方程计算结果绘制的方位反射系数变化曲面。为了说明计算结果的正确性，图1b中同时给出了基于Ruger近似解的方位反射系数变化曲面。不难看出，两组曲面变化趋势基本一致：随入射角θ增大，反射系数减小；随方位角增大，反射系数呈波浪状变化。为了能够更加清楚地对比两种方法的计算结果，将图1 所示三维方位反射系数分解为图2所示随方位角变化和图3所示随入射角变化的反射系数曲线。由图2可见，当入射角为0时，HTI介质弹性波反射／透射方程精确解和Ruger近似解相同，并且是一个常量，表明自激自收情况下反射系数与方位无关。当入射角分别是15°，25°和35°时，精确解和近似解相似并且近似为余弦曲线。这是由于HTI介质分别关于观测系统坐标系x，y，z轴对称，方位反射系数在方位角极坐标系下关于原点中心对称，体现在图2的直角坐标系下就类似于一条余弦曲线。因此，仅需分析方位角0～90°范围内的反射系数变化规律，即可掌握全方位角范围内的反射系数变化规律。由图3可见，当方位角分别是0，30°，60°，90°时，精确解和近似解随着入射角增大不断减小，并且二者相似度较高，这说明本文所得HTI介质弹性波反射／透射方程可以较为准确地反映地震波在HTI介质中的传播特征。

表1 双层介质模型［17］

表2 常见流体弹性参数［17］

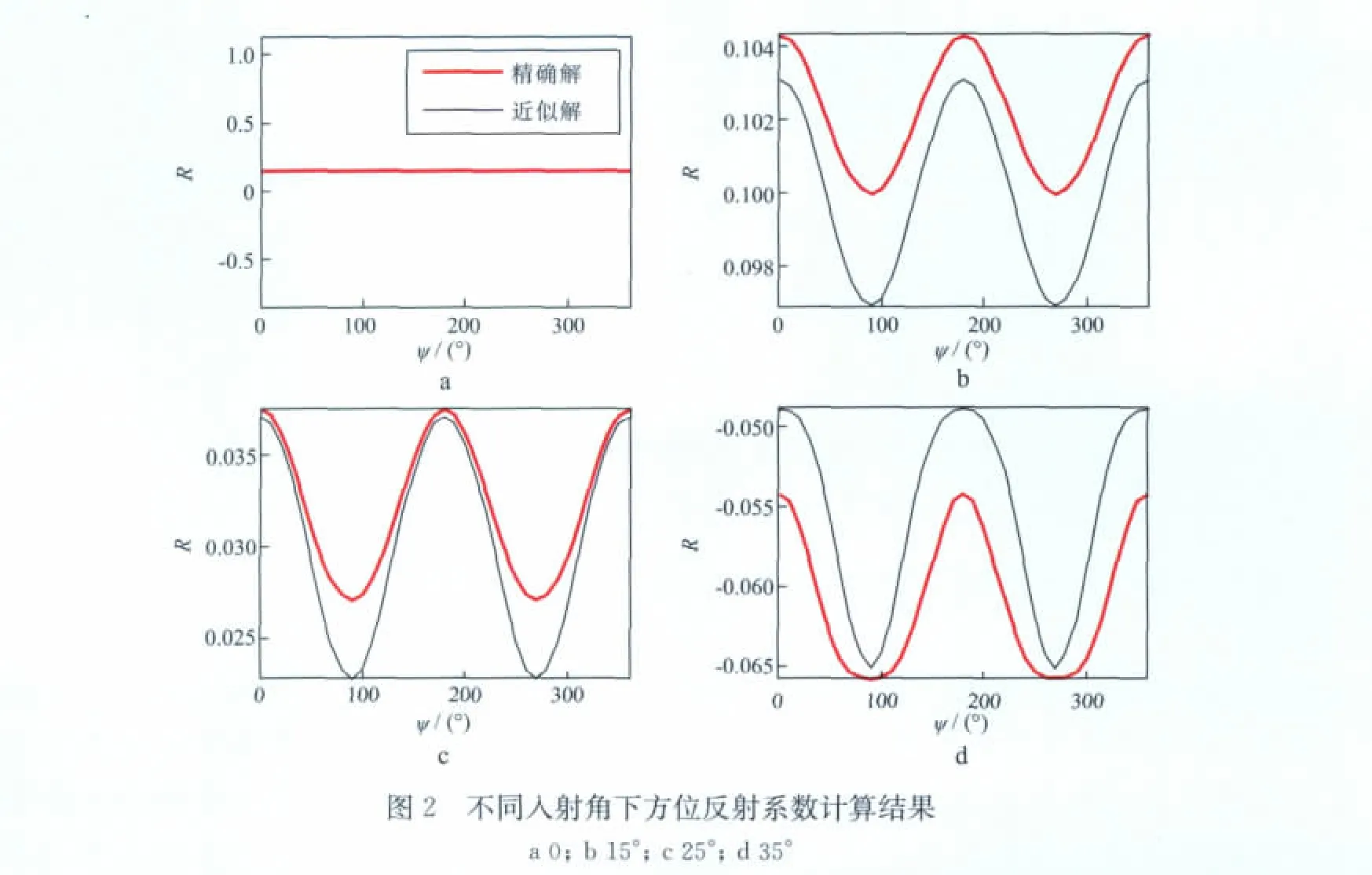
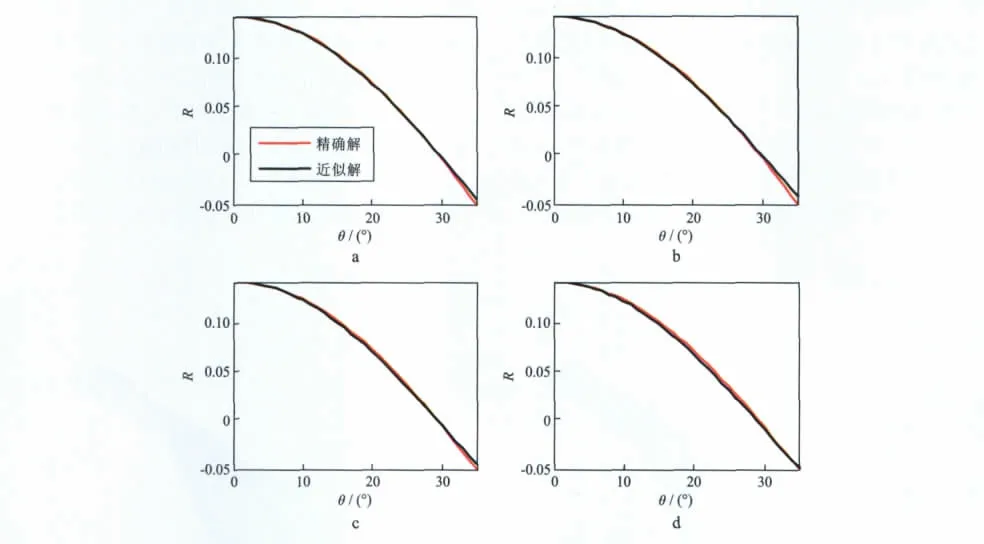
图3 不同方位角下反射系数计算结果

3.2 流体类型对方位反射系数的影响

为了研究流体类型对方位反射系数的影响，共设计了3种类型界面的双层模型，并假定上覆介质均为墨西哥湾黏土，下伏HTI介质为嵌入近垂直定向分布裂缝并且分别饱含水、油、气的黏土砂岩，裂缝密度和裂缝纵横比分别为0.1和0.001（参数见表1和表2），分别计算了入射角为0，15°，25°，35°的方位反射系数，结果如图4所示。

图4 上覆各向同性介质，下伏地层分别饱含水、油、气的HTI介质模型不同入射角的方位反射系数

由图4不难看出，分别饱含水、油、气的3 种HTI介质方位反射系数曲线形态基本一致，相比之下饱含水和饱含气的HTI介质反射系数差异大于饱含水和饱含油之间的差异。进一步求取饱含水和饱含气的HTI介质的反射系数绝对差（见图5），不难发现方位反射系数绝对差值大小与入射角密切相关。当入射角为0 时饱含水和饱含气的HTI介质方位反射系数绝对差是一个常数，说明自激自收的反射系数与方位角无关；随着入射角增大，反射系数绝对差增大。根据Shuey反射系数近似公式，上、下地层泊松比差越大，反射系数变化率随着入射角的变化也越大，下伏地层饱含气时比饱含水的泊松比差大，因此饱含气的反射系数下降速度比饱含水的大，表现为入射角越大反射系数绝对差也越大。进一步分析图5可见，在0～90°内，随着方位角增大反射系数绝对差减小，并且沿裂缝走向（90°方位）的绝对差最小，沿HTI介质对称轴方向（0方位）绝对差最大。这是由于HTI介质中地震波传播受裂缝影响，裂缝的存在使得地层泊松比发生改变，同时导致反射系数发生变化。

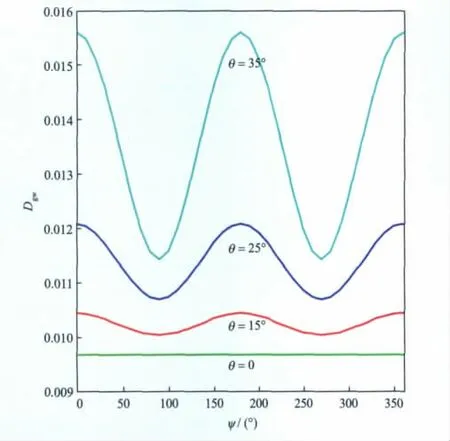
图5 上覆各向同性介质，下伏地层分别饱含水和气的HTI介质模型反射系数绝对差Dgw

3.3 裂缝密度对方位反射系数的影响

为了研究裂缝密度对反射系数的影响，采用前述方法设计了4种具有不同裂缝密度的HTI介质双层模型。同样假设上覆介质是墨西哥湾黏土，而下伏HTI介质为嵌入近垂直定向分布裂缝的饱含水黏土砂岩（参数见表1和表2）。图6为不同裂缝密度HTI介质方位反射系数计算曲线。显然，裂缝密度越大，方位反射系数随方位角变化越明显，且具有周期变化特点。对于同一方位角，裂缝密度越大，方位反射系数值越小，这是由于上覆墨西哥湾黏土速度小于下伏HTI介质，且裂缝密度越大相速度越小，反射界面上、下介质波阻抗差越小，进而使得反射系数减小。图7为裂缝密度分别为0.01和0.13时的反射系数绝对差，可以看出，随着入射角增大反射系数绝对差也在增大。这是由于下伏介质裂缝密度为0.13时的上、下介质泊松比差比裂缝密度为0.01时的大，因此裂缝密度为0.13 时的反射系数下降速度比裂缝密度为0.01时的大。此外，沿裂缝走向（90°方位）的反射系数绝对差最大，而沿对称轴方向（0方位）的反射系数绝对差最小，原因在于裂缝密度越大裂缝走向和HTI对称轴方向相速度差异越大，并且裂缝走向的相速度比HTI对称轴方向的大，使得裂缝走向反射系数绝对差比HTI对称轴方向的大。

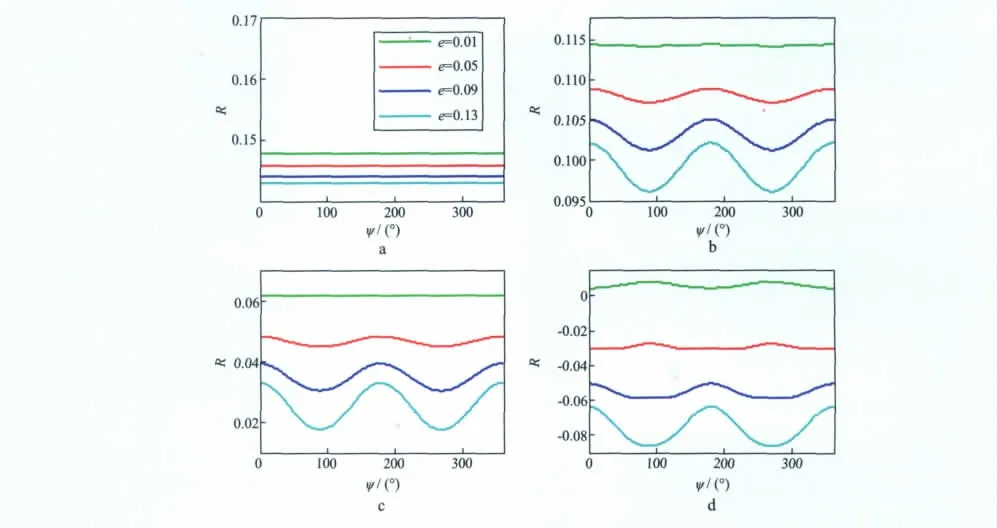
图6 上覆各向同性介质，下伏不同裂缝密度HTI介质模型的不同入射角方位反射系数

图7 上覆各向同性介质，下伏地层裂缝密度分别为0.01和0.13的HTI介质模型的反射系数绝对差Dc

4 结论

1）利用等效介质理论可以估算裂缝岩石背景介质骨架和饱和流体情况的弹性参数，结合Thomsen理论，可以构建HTI裂缝介质弹性矩阵；

2）根据HTI介质弹性矩阵、弹性波波动方程和弹性界面边界条件，可以推导出反映HTI介质弹性波传播特征的反射／透射方程；

3）下伏HTI介质分别饱含水和饱含气的反射系数差异大于饱含水和饱含油之间的差异，饱含气和饱含水反射系数差异随着入射角增大而增大，随方位角（0～90°）增大而减小；

4）下伏HTI介质裂缝密度越大，反射系数越小，不同裂缝密度的反射系数差异随着入射角增大而增大，随方位角（0～90°）增大也增大。

［1］Brown R，Korringa J.On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid［J］.Geophysics，1975，40（3）：608－616

［2］Cheng C H.Seismic velocities in porous rocks：direct and inverse problems［D］.Massachusetters：MIT，1978

［3］Cheng C H.Crack models for a transversely anisotropic medium［J］.Geophysical Research，1993，98（14）：675－684

［4］Hudson J A.Overall properties of a cracked soild［J］.Mathematical Proceedings of the Cambridge Philosophical Society，1980，88（2）：371－384

［5］Hudson J A.Wave speeds and attenation of elastic waves in material containing cracks［J］.Geophysical Journal of the Royal Astronomical Society，1981，64（1）：133－150

［6］Thomson L.Elastic anisotropy due to aligned cracks in porous rock［J］.Geophysical Prospecting，1995，43（6）：805－829

［7］Hill R.The elstic behavior of crystalline aggregate［J］.Proceeding of the Physical Society，1952，65（A）：349－354

［8］Hill R.Elastic properties of reinforced solids：some theoretical principles［J］.Journal of the Mechanics and Physical of Solids，1963，11（5）：357－372

［9］Hill R.A self－consistent mechanics of composite materials［J］.Journal of the Mechanics and Physical of Solids，1965，13（4）：213－222

［10］Kuster G T，Toksoz M N.Velocity and attenuation of seismic waves in two－phase media［J］.Geophysics，1974，39（5）：587－618

［11］Ruger A.Reflection coefficients and azimuthal AVO analysis in anisotropic media［D］.Colorado：Colorado School of Mines，1996

［12］Vavrycuk V，Psencik I.PP－wave refelction coefficients in weakly anisotropic elastic media［J］.Geophysics，1998，63（6）：2129－2141

［13］刘百红，杨强，石展，等.HTI介质的方位AVO 正演研究［J］.石油物探，2010，49（3）：232－240 Liu B H，Yang Q，Shi Z，et al.HTI media AVO forward research［J］.Geophysical Prospecting for Petroleum，2010，49（3）：232－240

［14］朱兆林，赵爱国.裂缝介质的纵波方位AVO 反演研究［J］.石油物探，2005，44（5）：499－504 Zhu Z L，Zhao A G.P－wave AVO research in crack media［J］.Geophysical Prospecting for Petroleum，2005，44（5）：499－504

［15］梁锴.TI介质地震波传播特征与正演方法研究［D］.东营：中国石油大学，2009 Liang K.The study on propagation feature and forward modeling of seismic wave in TI media［D］.Dongying：China University of Petroleum，1996

［16］Gassmann F.Elastic waves through a packing of spheres［J］.Geophysics，1951，16（3）：673－682

［17］Mavko G，Mukerji T，Dnorikin J.The rock physics handbook：tools for seismic analysis in porous media［M］.Cambridge：Cambridge University Press，1998：260－263