管输原油不可逆熵产分析
高东宇,熊小念,李 鹏,贾海洋
(1. 东北石油大学,黑龙江 大庆 163318; 2. .塔里木油田公司, 新疆 库尔勒 841000;3. 辽宁石油勘探局油田建设公司,辽宁 盘锦 124010; 4. 大庆油田工程建设公司油建公司,黑龙江 大庆 163000)
从熵的概念提出至今,它的应用领域远远超越了其热力学与统计物理学的范畴,而是进入到了天体物理、生物学及信息论中,甚至还深入到了社会科学中去。可以说,熵在各个学科领域都得到了极其广泛的应用。如熵可以通过最大熵原理对水环境模糊优化进行评价[1];也可通过气象熵来计算及分析降雨量的分布[2];还可通过农业熵来评价农业经济及农业技术的复合体系[3];甚至可以利用熵来描述人类社会组织结构的合理性及稳定性[4]。上述例子表明,熵科学的发展及应用已经深入到了各个学科领域当中,其重要性恰如爱因斯坦所说:“熵定律是科学定律之最。”熵产分析法是以熵概念为基础,结合传热学及流体力学的研究结果,得到实际体系中各部分的作功能力损失及熵增分布情况,并以最小熵产为前提,从设计及运行角度对系统进行优化[5]。本文从不可逆过程的熵产率着手,确定原油输送过程三种不可逆现象耦合作用的“力”和“流”的具体形式,研究管输过程的熵产率结构组成及变化规律,利用互唯象系数验证互相耦合的传热与传质的熵产率的准确性,并并将管输含蜡原油熵产率的计算结果与热经济的优化结果进行对比,来验证熵产率方程的实用性
1 熵产率数学模型
水平原油管道长l,内径为r,原油流量为Q,管道截面平均温度为T。管壁温度恒温且小于油温。为便于研究可作如下假设:①忽略剪切弥散与布朗运动;②忽略重力影响;③忽略热扩散和分子扩散④假设固体的比热容恒定。
文献[4]中给出了包括吉布斯方程、质量守恒方程、组元质量守恒方程及能量守恒在内的基本场平衡方程组,以这些基本方程组为基础,联立熵平衡方程,得到分别适合三种不可逆现象的熵产率方程,因熵函数具有可加性,系统的熵产率应为各不可逆过程的熵产率之和,从而得到适用于管输原油三种不可逆过程相互作用的总熵产率方程:
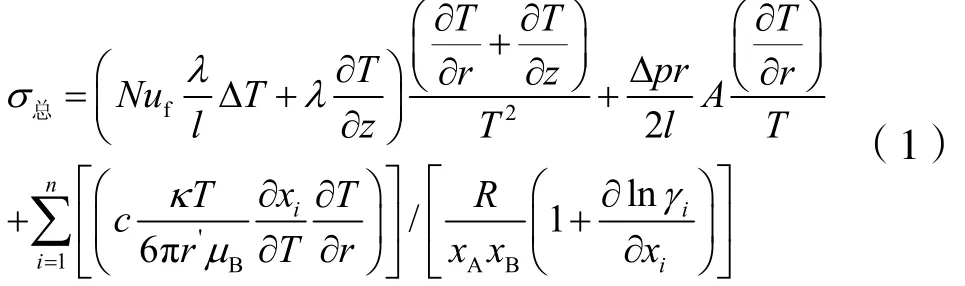
由式(1)可以看出:管输原油的熵产率由三部分组成[5]。第一部分表示反应率及亲和力之间的标量积,第二部分表示热流及温度倒数梯度的向量积,第三部分表示扩散流及化学势梯度减去体积力的向量积。概括的说就是:熵产率是“流”与“力”内积的总和。
由式(1)可以看出:管输原油的熵产率由三部分组成[5]。第一部分表示反应率及亲和力之间的标量积,第二部分表示热流及温度倒数梯度的向量积,第三部分表示扩散流及化学势梯度减去体积力的向量积。概括的说就是:熵产率是“流”与“力”内积的总和。
依据总熵产率的计算模型得到总熵产率的变化趋势如图1所示。

图1 传热、粘滞及传质熵产率对总熵产率的影响Fig.1 The impact of heat transfer, viscous and mass transfer entropy production rate on total entropy production rate
由图1可以看出,粘滞力引起的熵产率随输油温度的降低而升高,传热引起的熵产率随输油温度的降低而下降,传质引起的熵产率随温度的降低先下降后升高;总熵产率也是先下降后升高,输油温度较高时,三者之中对总熵产率贡献最大的是传质熵产率,随着温度的降低,传热熵产率下降幅度比传质熵产率缓慢,导致总熵产率中起主要作用的是传热熵产率。粘滞熵产率在管输过程中相对于传热以及传质熵产率较小,并且温度高于 50 ℃时粘滞力熵产率几乎为零。
根据之前所得到的含蜡原油管输过程的熵产率的计算公式,得到了熵产率随温度的变化曲线,下面讨论流量、管径以及保温层厚度的变化对总熵产率的影响如图2、3及4所示。

图2 管径变化对熵产率的影响Fig.2 The impact of diameter on the entropy production rate

图3 输量变化对熵产率的影响Fig.3 The impact of transmission capacity on the entropy production rate
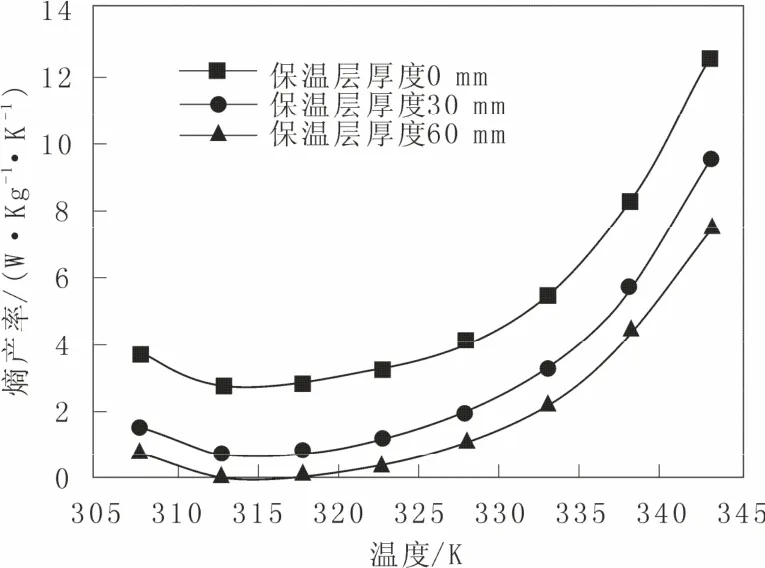
图4 保温层对熵产率的影响Fig.4 The impact of insulation layer on the entropy production rate
由图2,总熵产率随温度的下降先降低后升高,最小熵产率发生在 40 ℃ 左右。随油流温度的降低,最小熵产率随管径的增大而降低。即输送同样的原油,采用大管径的管道时,可以采用较低的输油温度。
由图3可知,输量对熵产率有一定的影响。输量越高,输送单位质量原油的熵产率就越低,但随输量的增加,熵产率降低的幅度逐渐减少;只有适当的原油温度才能保证单位质量原油输送单位距离所产生的熵产率最小。
2 唯象系数的数学模型
一般的,一种“力”可能推动几种“流”;一种“流”也可能是几种“力”共同推动的结果。也就是说,产生某种流的不一定只有它的共轭力,有时还可能有其他的力。“流”与“力”是否可以耦合要依“流”与“力”的张量特性而定。在熵产率方程中,传热和传质的是矢量,粘性流动的则是张量。根据居里原理:在各向同性的系统(即系统处于平衡态时,各方问只有相同的性质)中,相差奇数阶的张量的“流”与“力”将不能耦合[6]。由此可知在上述的熵产率方程中,属于同阶张量的热—质传递的“流”与“力”可以互相耦合,故二者相互耦合的唯象系数分别为:
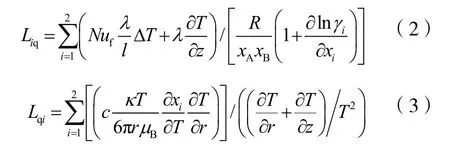
传质与传热之间的互唯象系数的关系如图5所示。
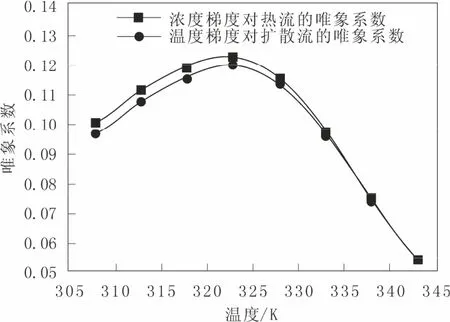
图5 互唯象系数随温度的变化Fig.5 The variation of mutual phenomenological coefficient with temperature
由图 5,传热与传质之间的互唯象系数在数值上大致相等,满足昂色格倒易定律,也就间接的证明了上述熵产率方程的准确性。但在数值上可以看出,互唯象系数比自唯象系数小很多,只是自唯象系数的2%左右
3 与经济分析结果的对比
原油在加热输送过程中,加热温度的升高会导致散热速度加快,即造成更多的燃料消耗;若降低管输原油的加热温度,虽然燃料消耗会减少,但摩擦阻力会增大却会导致更多的泵功耗[7]。因此,管输原油过程需要平衡燃料消耗与泵功耗的费用问题,即动力费用与热力费用的平衡问题[8]。
动力费用:

热力费用:

管道运行总费用:

计算管输过程原油的费用随温度变化趋势如图6所示。

图6 油温对管输过程总费用的影响Fig.6 The impact of the oil temperature on the total cost of the pipeline process
由图1和图6的对比中可以看出:热经济优化结果与熵产率最小的优化结果相同,二者都是最佳的输油温度与最低的管道运行费用相对应,只是热经济优化受诸多因素的影响,如保温材料、电价格以及燃料价格率等,所以尽管热经济优化结果比较直观,但是它会随时随上述因素的影响而发生波动,因此不好控制其最有结果。而原油管输过程熵产最小优化设计结果只与管道的保温层厚度和管径及输量有关,其结果不受当前物价等的影响,由此看出,熵产最小的优化结果比热经济优化的设计结果更具适用性。
4 结束语
本文针对传热、传质以及粘滞耦合作用的原油管输蜡沉积过程,分别研究这三种不可逆现象所对应的熵产率变化规律。粘滞力导致的熵产率随输油温度的降低而升高,传热导致的熵产率随输油温度的降低而下降,传质扩散导致的熵产率随温度的下降先降低后升高;总熵产率也是随温度的下降先降低后升高,最小熵产率发生在40 ℃左右。
总熵产率中传热和传质熵产率作用相当,粘滞熵产率的作用最小。利用互唯象系数验证互相耦合的传热与传质的熵产率的准确性,并将热经济优化结果与熵产率分析结果进行对比,都是最佳的输油温度对应最低的管道运行费用,但熵产率的优化设计不像热经济优化结果那样依赖于材料价格等因素。由此可见,熵产率分析结果比热经济优化的设计结果更具适用性,值得在原油管输过程的的优化设计中推广应用。
[1] 王栋.基于最大熵原理的水环境模糊优化评价模型[J]. 河海大学学报,2002, 30(6): 56-60.
[2]艾南山, 顾恒岳. 泛系地貌学初论[J]. 重庆交通学院学报, 1970, 3(2):72-80.
[3]赵文桐, 陈霞, 赵佩章. 信息熵与气象熵[C]. 熵与交叉科学研讨会论文集, 新疆, 1987: 127-129.
[4]郑龙翔, 邹光勇. 农业生态系统中的熵[J]. 环境污染与防治, 1900,(12): 2-5.
[5]杨东华. 不可逆过程热力学原理及工程应用[M]. 科学出版社,1989:23-25.
[6] J.R. Welty, C.E. Wicks, R.E. Wilson. Fundamentals of Momentum, Heat,and Mass Transfer [M]. 2005, pp:322.
[7]盖平原. 稠油管输起始加热温度熵产最小优化设计[J]. 油气储运,2011, 30(7): 501-504.
[8]王平, 汪国业, 田艺兵,等. 结蜡厚度对输油成本的影响[J]. 石油化工高等学校学报, 2002, 15(1): 47-50.

