小行星着陆装置着陆动力学及着陆性能分析

赵志军 赵京东 刘 宏

(哈尔滨工业大学 机器人技术与系统国家重点实验室，哈尔滨150080)

小行星着陆装置用于实现小行星的本地探测，使得探测小行星可以像探测月球、火星等大行星一样通过投放着陆器来进行.根据着陆器携带仪器设备的不同，可以对小行星展开多方面的研究，如介质特性、温度传导特性、环境特点等，加深对小行星的认识，为下一步开发利用小行星提供科学依据，促进空间科学技术的发展[1].可以将一定的推进装置通过着陆装置固定在小行星表面来改变其运行轨道，避免小行星撞击地球[2].小行星轨道特性多样化，其在轨道上有大的倾斜度和倾角，如果将仪器设备通过着陆装置固定在小行星表面，小行星将成为研究太阳和其他星体的有力平台[3].可见小行星着陆装置研究意义深远.

着陆时的动力学特性及稳定性是着陆装置重要的性能指标，是着陆装置研究的关键问题.通过着陆动力学及稳定性研究，可以分析着陆时的速度、角速度、加速度等动力学参数的变化特性，分析不同着陆条件下的着陆稳定性，从而指导着陆器的设计或着陆初始条件的选择，改善着陆性能.南京航空航天大学对小行星着陆器的着陆动力学及稳定性进行了一定的研究[4];ESA(Europe Space Agency)对Rosetta彗星着陆器的着陆动力学及稳定性采用Simpack软件进行了仿真分析[5];此外，NASA(National Aeronautics and Space Administration)在Apollo月球着陆器研究阶段，进行了大量的着陆动力学及稳定性研究[6－7];国内的哈尔滨工业大学[8－9]，南京航空航天大学[10]，中国空间技术研究院[11]及其他研究院所[12－13]在对月球着陆装置的着陆动力学及稳定性进行了大量研究，取得了丰硕成果.目前着陆装置着陆动力学及稳定性研究的基本思路是:根据着陆装置结构特点建立着陆动力学及稳定性数学模型，经过对模型的分析，得出着陆动力学及稳定性特性，再通过仿真或实验对模型分析的正确性进行验证.

小行星着陆装置在结构特点及着陆策略方面与月球、火星着陆装置存在较大区别，其着陆动力学及着陆性能亦有所不同.本文在分析目标小行星特性、着陆装置特点及着陆策略的基础上，基于Lagrange法对着陆动力学特性进行了描述，并通过仿真分析方法对着陆性能进行了研究.

1 小行星及着陆装置特点分析

小行星与月球、火星等大星体相比，具有表面引力弱，介质特性未知，地貌崎岖不平等特点.不同组成成分的小行星，具有不同的反照率，据此将小行星分为c，S，M等10多种类型[14].在各类小行星中，一般认为C类小行星的组成与碳质球粒陨石(一种石陨石)相似，碳质球类陨石含有碳质，且水、硫、稀有气体等化合物含量较高，通常都含有多种有机化合物，如氨基酸，其矿物学和岩石学特性中缺乏游离的金属或含量很低，其可能含有太阳系形成之前的物质[15].可见C类小行星所含物质原始，是研究太阳系起源的理想对象，且强度低、易锚固，是小行星着陆器着陆的理想选择.

本文所述小行星着陆装置针对C类小行星设计，目标小行星介质最大允许切变强度小于5 MPa.小行星着陆装置设计难点主要体现在微重力环境下着陆装置的反弹、飘走，着陆时的滑移及对未知地形的适应性.小行星着陆装置如图1、图2所示，质量属性如表1所示.

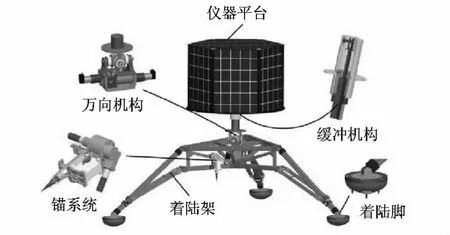
图1 小行星着陆装置示意图

图2 小行星着陆装置

表1 小行星着陆装置质量属性

机械结构包括着陆脚、锚钉、着陆架、万向机构、缓冲机构、仪器平台、锚系统等部分.该着陆装置可以实现微重力环境下的着陆及锚固，其具有以下特点:

1)设计有锚系统.锚系统为着陆装置在小行星表面提供长期锚固，防止着陆后相当长时间内着陆装置的飘走.

2)设计有锚钉.锚钉安装在着陆脚底部，长度约为10 cm.C类小行星主要成分为碳质球类陨石，且可能含有有机物，表面介质较软但不松散，有一定强度(太松散的表层介质由于微重力及高速旋转的离心力不可能在小行星表面存在).着陆时在初始撞击及反推火箭作用下锚钉被压入小行星表面一定深度，此举可以增大着陆脚与着陆面之间的摩擦系数，防止着陆装置发生滑移，同时为着陆装置提供一定的锚固力.

3)设计有万向机构.万向机构一方面缓冲着陆时水平方向的撞击冲量，另一方面在着陆后对仪器平台的姿态进行调整，以适应小行星的崎岖地形，利于其上仪器设备展开探测.

4)缓冲机构置于仪器平台下方.保证仪器平台在竖直方向具有良好的缓冲效果，缓冲机构设计的过载加速度小于10g[16].

5)采用三腿可折叠桁架式结构.该结构质量轻、体积小.在微重力环境下，着陆装置着陆时间长，控制系统有充裕时间对其着陆姿态及速度进行控制调整，以保证小的着陆速度及理想的着陆姿态，因此对着陆装置的结构强度要求较低，所以着陆腿采用可折叠桁架式结构.

6)反推火箭.反推火箭置于仪器平台顶部，属于姿态控制系统，不属于着陆装置机构部分，文中未有图示.其在着陆阶段具有重要作用，是成功着陆不可或缺的部分.在着陆下降阶段，反推火箭实现对着陆装置速度及姿态的控制，以实现接近理想的着陆速度及着陆姿态，在着陆撞击阶段，反推火箭实现对着陆装置的下压作用，防止着陆装置反弹.

2 着陆动力学分析

着陆装置经轨道器释放后在导航、控制系统作用下接近小行星，然后完成在小行星表面的着陆.着陆脚接触小行星瞬间，着陆装置与小行星表面之间发生极其复杂的接触响应，该接触响应的力矢量在三维空间的计算目前还没有完善的分析方法，本文不对其进行研究.本文只对着陆装置初次撞击后到第一次翻转结束之间的动力学特性进行分析，该阶段是着陆过程的核心阶段，其动力学参数足以描述着陆装置的着陆性能及指导结构设计.由于三维着陆动力学模型极其复杂，且二维着陆动力学模型可对着陆性能进行较好的描述，目前月球、火星着陆器的动力学模型以二维平面模型为主.三腿式着陆装置以1-2、2-1模式着陆时，在过第1接触点且垂直着陆面的平面内发生翻转，可简化为二维模型;以1-1-1模式着陆时，可认为其发生两次平面翻转，同时二维模型在三腿式月球、火星着陆装置中广泛使用[6].所以本文通过二维动力学模型对小行星着陆装置的着陆特性进行分析.

2.1 着陆策略

着陆装置的着陆速度较小，横向不大于0.5 m/s，纵向不大于1.5m/s，着陆时不会发生高速撞击，所以着陆器的反弹及滑移易于控制.着陆装置撞击小行星瞬间，缓冲机构及万向机构吸收仪器平台所受撞击冲量，同时着陆脚内的接触开关产生触发信号.控制系统接收到该触发信号后控制锚系统发射及仪器平台顶部的反推火箭点火，该反推火箭为着陆装置提供指向着陆面的推力，防止着陆装置反弹.着陆脚上的锚钉在初始撞击及反推火箭推力作用下被压入C类小行星表面，阻止了着陆装置在着陆面上滑移.初次撞击后着陆装置将绕与小行星接触的着陆脚发生翻转，翻转过程中反推火箭维持恒定推力约5 s，锚系统快速卷线.当3个着陆脚完全与着陆面接触后翻转结束，着陆完成.然后根据需要通过万向机构对仪器平台姿态进行调整，即可展开对小行星的探测.

2.2 二维着陆动力学

根据C类小行星及着陆装置的特点，建立动力学模型时做如下简化:①小行星表面为微重力，重力加速度数量级约为10－4m/s2，所以忽略小行星表面重力加速度;②着陆脚与着陆腿之间为铰接，摩擦系数较小，不计该处的摩擦;③着陆架刚度远大于缓冲机构竖向刚度及万向机构旋转刚度，所以忽略着陆架的柔性;④锚系统发射的锚体质量约为80 g，速度约为50 m/s，着陆装置质量约为100 kg，且有反推火箭提供推力，所以忽略锚系统发射对着陆装置的反冲作用;⑤锚系统拉紧线绳时间约为5 s，着陆翻转过程小于2 s，所以翻转过程中锚系统线绳尚未拉紧.

撞击后着陆装置绕O点翻转，如图3下所示，其具有3个自由度，分别为m1的转动，m2的转动，m2随缓冲机构的平动.可采用Lagrange法建立其动力学方程，动能、势能及瑞利耗散函数如式(1)、式(2)所示.

可得Lagrange动力学方程如式(3)～式(5)所示，式中各参数意义如图3中所示.

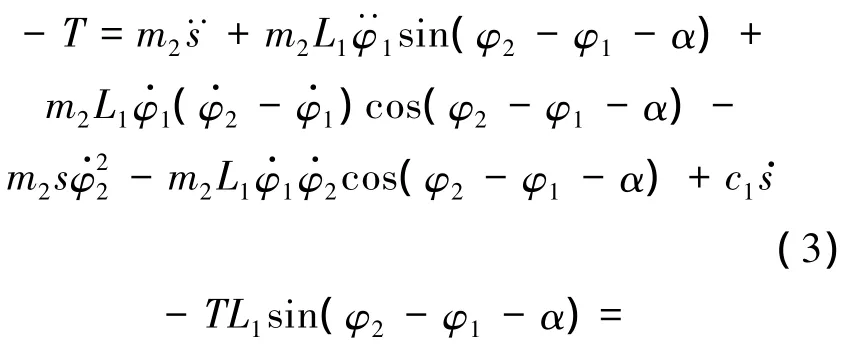
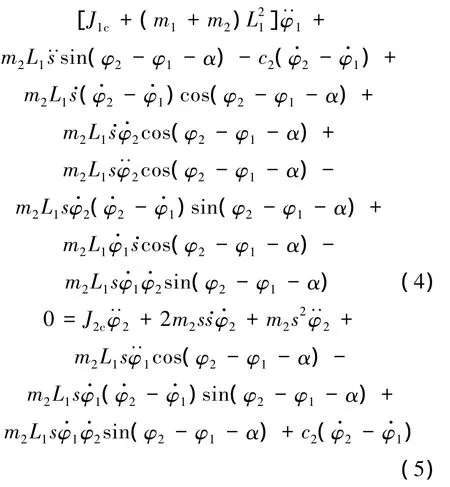
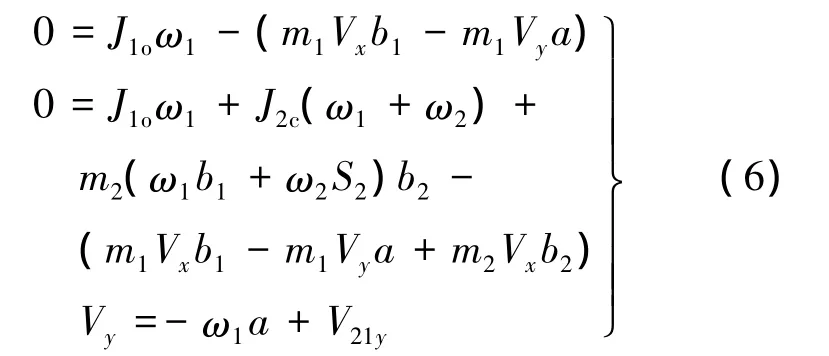
由方程式(6)可求得ω1，ω2，V21y，即为着陆装置着陆撞击后翻转运动的初始值.

2.3 动力学模型正确性验证

当着陆装置以初始速度Vx=－0.5 m/s，Vy=－1.5 m/s着陆于θ=30°着陆斜面时的值如图4～图6所示.“数据3”虚线所示为上述动力学方程求解结果，“数据1”实线所示为与着陆装置对应的二维模型在Adams中着陆仿真结果，“数据2”点划线所示为上述动力学方程利用“数据1”实线中的初值进行求解的结果.

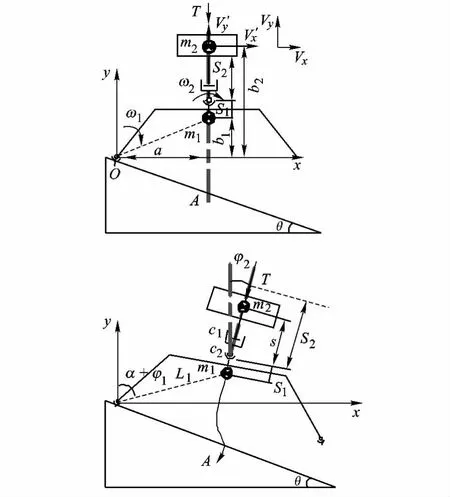
图3 着陆撞击及翻转示意图

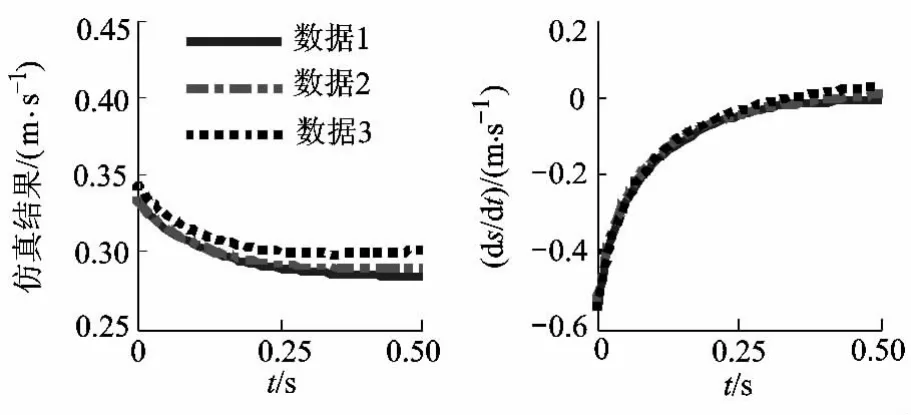
图4 s和的方程求解及Adams仿真结果

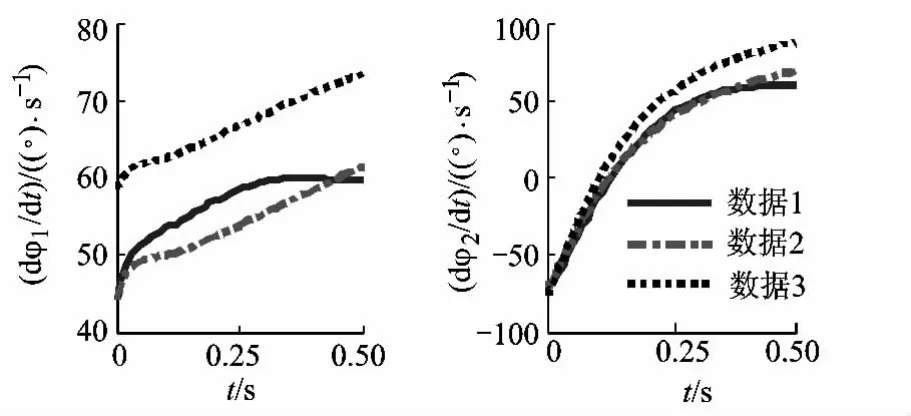
图5 1和2的方程求解及Adams仿真结果

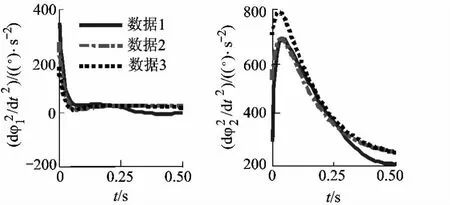
图6 1和2的方程求解及Adams仿真结果

图4～图6中各组曲线较为接近且具有一致的变化趋势，各组曲线相互之间误差分析如表2所示.可见本文提出的Lagrange动力学模型可以较为准确的描述着陆装置的着陆动力学特性，同时表明初始值对动力学方程求解有较大影响.由于着陆装置不发生反弹，所以动力学模型的初始值计算未考虑着陆脚与着陆面之间的接触模型，Adams仿真时软件自身考虑了接触模型，导致本文计算的初始值与Adams仿真初始值之间存在误差.

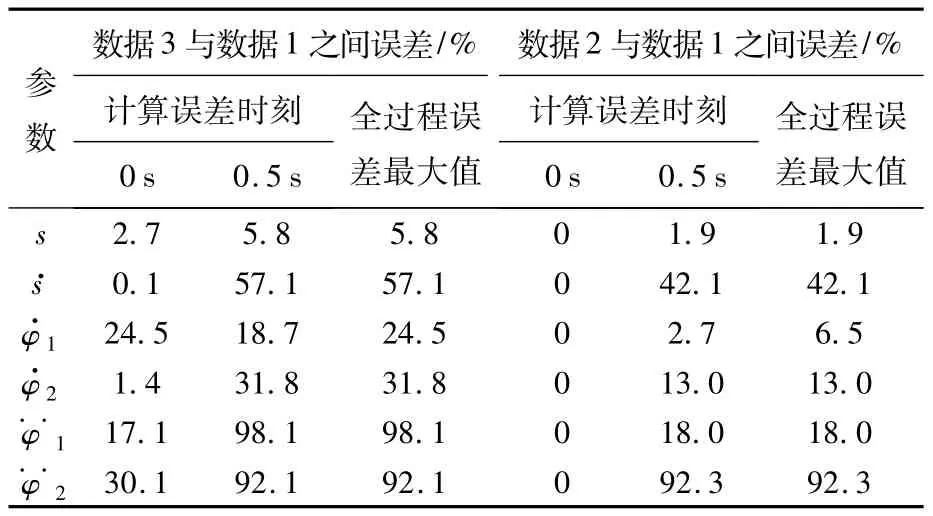
表2 方程求解与仿真结果误差分析

3 着陆性能研究

过载加速度及着陆稳定性是衡量着陆装置性能的关键指标，过载加速度太大容易造成仪器设备损坏，着陆不稳定会造成着陆装置翻倒，都将导致着陆失败，本文所述的着陆性能即指上述两方面.采用Adams仿真的方法，对多种着陆速度及偏航角条件下在最大允许倾斜表面着陆时的性能进行统计分析.分析具有普遍性及代表性，可以对着陆装置的着陆性能进行较好的评估.

3.1 仿真条件

着陆装置的着陆姿态定义如图7所示，定义Oixiyizi为惯性坐标系，Olxlylzl为机体坐标系，将xl轴绕Zi轴旋转的角度定义为偏航角，xl轴绕yi轴旋转的角度定义为俯仰角，zl轴绕xi轴旋转的角度定义为翻滚角，定义顺时针方向为正.

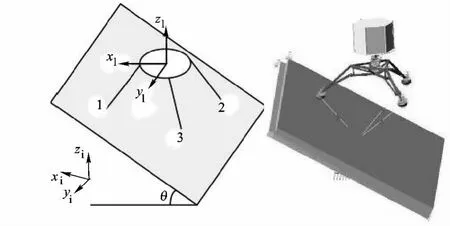
图7 着陆姿态示意图

仿真参数定义如表3所示，着陆装置下部质量m1指表1中着陆脚、着陆架、万向机构等组成的质量，约为22 kg;着陆装置上部质量m2包括表1中缓冲机构、仪器平台质量及着陆装置承载的负载质量，共计约78 kg;由于设计有锚钉，着陆时锚钉可以穿透C类小行星表面，造成较大的摩擦系数，参照Rosetta彗星着陆器着陆仿真将着陆面摩擦系数取为2.0;缓冲机构阻尼、万向机构等效阻尼、反推火箭推力是着陆装置的固有设计参数;在较硬的表面着陆更能检验着陆性能，所以将着陆面接触刚度取为月球表面接触刚度的2倍[11].

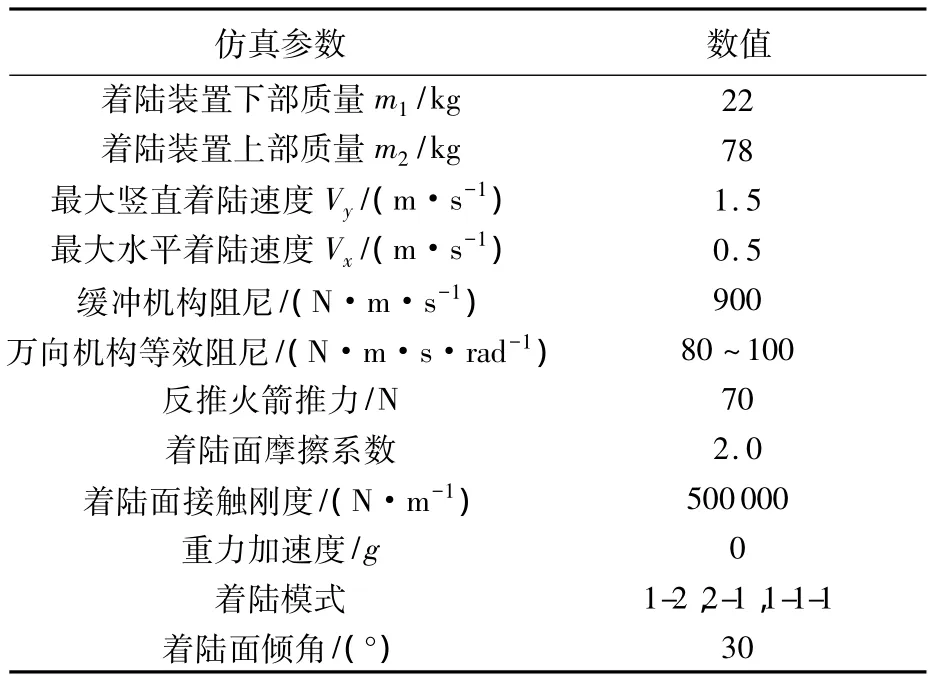
表3 着陆仿真参数

3.2 着陆性能仿真分析

着陆装置水平方向最大允许合速度为0.5 m/s，竖直方向最大允许合速度为1.5m/s，最大允许着陆面倾角为30°.仿真分析时，着陆面倾角为30°，翻滚角及俯仰角为0°，偏航角从0°以10°步长递增到120°，产生13种着陆姿态(第13种姿态与第1种姿态在理论上是同一种姿态)，每种着陆姿态具有10种代表性的着陆速度，分别为(－0.5，0，－1.5)、(0.5，0，－1.5)、(0.2，0.2，－1.5)、(0.4，0.4，－1.5)、(0.5，0.5，－1.5)、(0.6，0.6，－2)、(－0.2，0.2，－1.5)、(－0.4，0.4，－1.5)、(－0.5，0.5，－1.5)、(－0.6，0.6，－2)，单位为m/s.因此，可以得到130种着陆条件下的着陆性能.

图8所示为着陆装置在上述多种着陆条件下着陆时的最大过载加速度.可见，当着陆速度达到(0.5，0.5，－1.5)或(－0.5，0.5，－1.5)时，最大过载加速度接近10g，此时水平方向合速度为0.707 m/s，大于水平方向允许着陆速度0.5 m/s;当着陆速度为(0.6，0.6，－2)或(－0.6，0.6，－2)时，最大过载加速度大于10g，此时水平方向着陆速度已远大于允许的着陆速度.图9所示为着陆装置在上述多种着陆条件下着陆时的着陆稳定时间，即从开始着陆到停止翻转所需的时间.为便于描述，将着陆不稳定时的稳定时间取为10 s.可见，只有在(－0.6，0.6，－2)速度下着陆时，会出现着陆不稳定的状态，其他着陆条件下的着陆稳定时间均小于5 s，可以稳定着陆.

综上所述，着陆装置在允许的着陆速度范围内，以不同着陆姿态着陆时，其最大过载加速度均小于10g，着陆稳定时间均小于5 s，着陆装置具有良好的着陆性能.同时可知着陆装置在偏航角为60°，即采用2-1着陆模式时，具有最小的过载加速度及最短的着陆稳定时间，具有最佳的着陆性能.

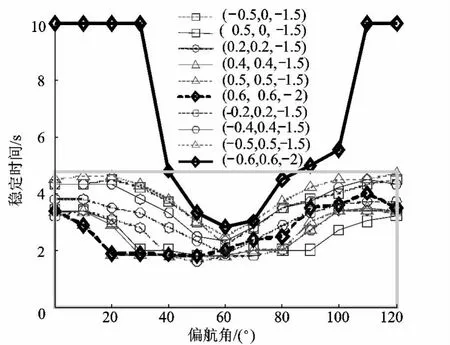
图8 不同着陆速度下偏航角对过载加速度影响

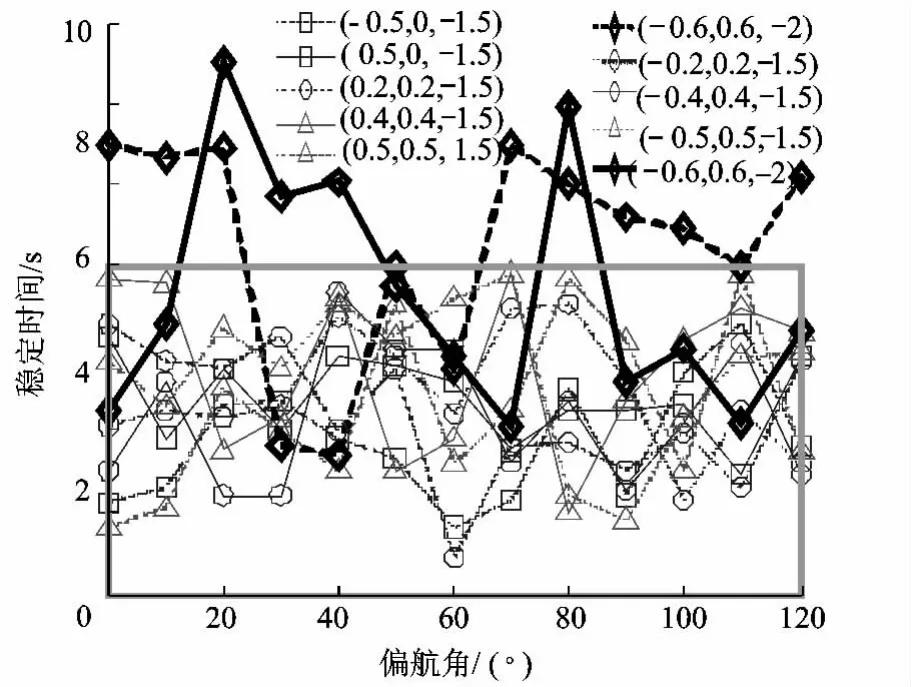
图9 不同着陆速度下偏航角对着陆稳定时间影响

4 结论

1)提出了采用Lagrange方程建立二维着陆动力学模型的方法，实现对着陆装置翻转阶段动力学特性的描述.模型求解与仿真分析结果接近且具有一致变化趋势，可较为准确的描述着陆装置的着陆动力学特性.该模型也可应用于其它具有相似结构的着陆装置分析中.

2)采用仿真方法，对着陆装置在130种着陆条件下的着陆性能进行了统计分析.在最大允许倾角30°斜面上，着陆装置以水平方向≤0.5 m/s，竖直方向≤1.5 m/s着陆时，过载加速度小于10g，着陆稳定时间小于5s，具有良好的着陆性能，且以偏航角为60°即2-1模式着陆时着陆性能最佳.

References)

[1]Binzel R P，Lupishko D，Martino M D，et al.Asteroids III:physical properties of near-earth objects[M].Tucson:University of Arizona Press，2002:255－271

[2]Chapman C R.The hazard of near-earth asteroid impacts on earth[J].Earth and Planetary Science Letters，2004(222):1－15

[3]Blessing M，Quintana E，Persaud R，et al.Asteroids working group report[C]//Next Generation Exploration Conference 2006，2006

[4]吴志斌.小天体着陆器附着机构设计研究[D].南京:南京航空航天大学航空宇航学院，2008

Wu Zhibin.Investigation of attaching technology for a small body lander[D].Nanjing:Institute of Technology of Aeronautics and Astronautics，Nanjing University of Aeronautics and Astronautics，2008(in Chinese)

[5]Hilchenbach M，Kuchemann O，Rosenbauer H.Impact on a comet:rosetta lander simulations[J].Planetary and Space Science，2000(48):361－369

[6]Lavender R E.Touchdown dynamics analysis of spacecraft for soft lunar landing[R].NASA TN D-2001，1964:1－32

[7]Herr R W，Leonard H W.Dynamic model investigation of touchdown stability of lunar-landing vehicles[R].NASA TN D-4215，1967:1－22

[8]Wang Shaochun，Deng Zongquan，Hu Ming，et al.Dynamic model building and simulation for mechanical main body of lunar lander[J].Journal of Central South University，2005，12(3):329－334

[9]王闯，刘荣强，邓宗全，等.月球着陆器着陆过程动力学分析[J].北京航空航天大学学报，2008，34(4):381－385

Wang Chuang，Liu Rongqiang，Deng Zongquan，et al.Dynamics analysis of lunar lander's landing process[J].Journal of Beijing University of Aeronautics and Astronautics，2008，34(4):381－385(in Chinese)

[10]Chen Jinbao，Nie Hong.Overloading of landing based on the deformation of the lunar lander[J].Chinese Journal of Aeronautics，2008(21):43－47

[11]蒋万松，黄伟，深祖炜，等.月球探测器软着陆动力学仿真[J].宇航学报，2011，32(3):462－469 Jiang Wansong，Huang Wei，Shen Zuwei，et al.Soft landing dynamic simulation for lunar explorer[J].Journal of Astronautics，2011，32(3):462－469(in Chinese)

[12]逯运通，宋顺广，王春洁，等.基于刚柔耦合模型的月球着陆器动力学分析[J].北京航空航天大学学报，2010，36(11):1348－1352

Lu Yuntong，Song Shunguang，Wang Chunjie，et al.Dynamic analysis for lunar lander based on rigid flexible coupled model[J].Journal of Beijing University of Aeronautics and Astronautics，2010，36(11):1348－1352(in Chinese)

[13]龙铝波，卿启湘，文桂林，等.基于ADAMS的着陆器软着陆稳定性仿真分析[J].工程设计学报，2010，17(5):334－387

Long Lubo，Qing Qixiang，Wen Guilin，et al.Simulation analysis of lander soft landing stability based on ADAMS[J].Journal of Engineering Design，2010，17(5):334－387(in Chinese)

[14]Lupishko D F，Martino M D.Physical properties of near-earth asteroids[J].Planet Space Sci，1998，46(1):47－74

[15]王道德.陨石类型简介[J].地球与环境，1980(2):9－18

Wang Daode.Meteorolite classification introduction[J].Earth and Environment，1980(2):9－18(in Chinese)

[16]Alazzam N，Banks B，Burke J，et al.Lunar landing gear[R].Queen's University，Kingston Ontario，Canada，2009