盘绕式伸展臂展开模式的力学原理

韩建斌 王新升 马海波

(北京航空航天大学 宇航学院，北京100191)

盘绕式伸展臂是一种空间伸展臂，靠纵杆的螺旋变形来实现展开和收拢的，可用于太阳电池阵、太阳帆、探测臂等空间伸展机构［1-3］.在中心绳索控制下，伸展臂有2种展开模式［4］:螺旋展开和逐层展开.处于螺旋状态的伸展臂极不稳定，其侧向弯曲刚度很差.形成逐层展开模式后，刚度较好［5］，是盘绕式伸展臂展开的理想状态.

对于盘绕式伸展臂已经有一些分析研究［5-6］.但由于纵杆的大变形及整个系统的复杂性，对其进行变形分析仍然是一个难点.普通的有限元分析和微分方程并不适用于盘绕式伸展臂的展开特性研究［7］.Kirchhoff动力学比拟理论是研究细长弹性杆超大变形的有效工具，利用Kirchhoff动力学研究圆柱面约束的弹性杆问题已有很多研究［8-11］，因此利用Kirchhoff动力学可以分析纵杆的变形.此外，为了简化问题，可以假设伸展臂伸展过程足够缓慢，因此可以忽略伸展过程的动力学效应［10］.本文针对三角形横框铰接盘绕式伸展臂进行了研究，提出了伸展臂展开模式的判据，最终得到伸展臂构型和展开模式之间的关系.

1 盘绕式伸展臂变形的几何分析

盘绕式伸展臂的两种展开模式见图1.将小范围内纵杆的变形分为螺旋(螺旋角在0～90°之间)和伸直(螺旋角接近0°，且保持稳定)2种状态，如图1所示.

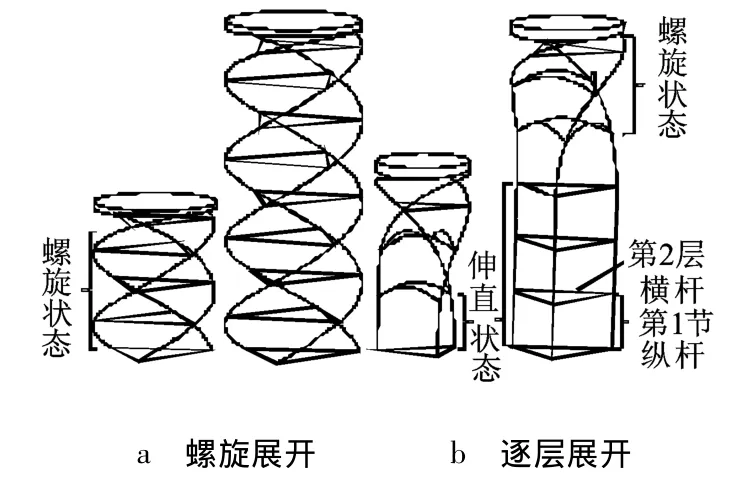
图1 盘绕式伸展臂的2种展开模式

为方便后文描述，定义如下:每两个横框之间的纵杆为一节，向上依次标记为第 1，2，3，…，n节;第1节纵杆上部的横杆标记为第2层横杆，向上依次标记为第 3，4，5，…，n 层.

认为盘绕式伸展臂变形过程中斜拉索长度不变，而横杆可以弯曲.假设一节伸展臂以均匀螺旋方式盘绕，其几何变形如图2所示.

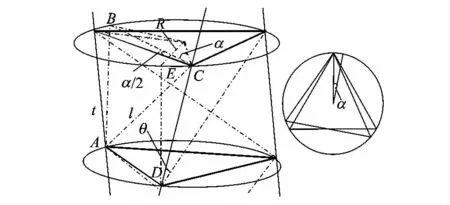
图2 盘绕式伸展臂几何关系示意图

图2中，α为伸展臂相邻两个横框间的相对扭转角;t为伸展臂节距;R为盘绕半径;θ为纵杆螺旋角，是纵杆轴向切线与伸展臂轴向的夹角;l为斜拉索长度.其中t，l为恒值.

在直角三角形ABC中有

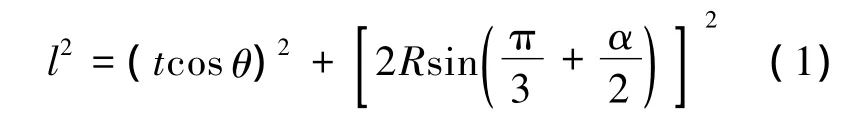
圆柱面上的区域CED部分是直角三角形CED沿圆柱面弯曲后的形状.因此有

设螺旋角为0时伸展臂半径为 R0.得到t/R0=1.5时，R/R0随螺旋角θ变化的曲线见图3.

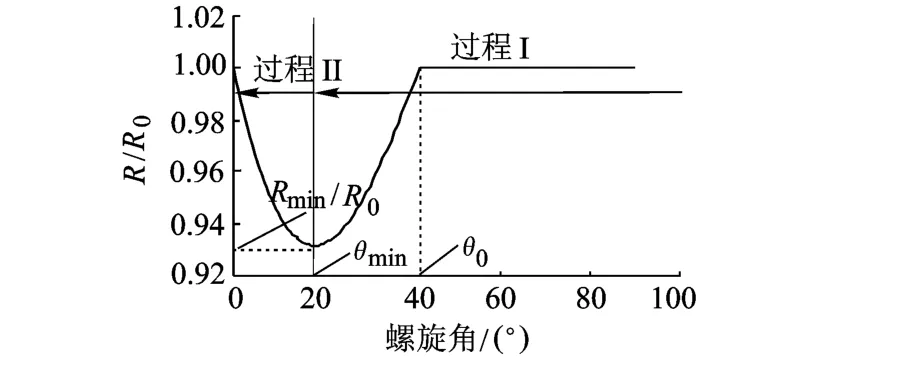
图3 在斜拉索限制下伸展臂半径随螺旋角变化

设螺旋角等于θmin时，盘绕半径的最小值为Rmin.此时横杆两端距离

可见盘绕式伸展臂伸展时，纵杆压缩横杆至其两端距离为dmin，之后横杆释放能量，推动纵杆伸展.文献［6］将这一现象叫做“snap through”.因此横杆的弯曲刚度对伸展臂的展开有一定影响.

2 盘绕式伸展臂展开模式的判据

2.1 横杆弯曲刚度的影响

以表1所示NASA的ST8(Space Technology 8)任务中使用的盘绕式伸展臂(简称ST8伸展臂［12-13］)为对象，在Adams中建立仿真模型，如图4所示.

根据第1节所述，单节纵杆在伸展到一定长度时，需要压缩横杆，因此展开速度会变慢.此时上面一节纵杆开始伸展.即盘绕式伸展臂展开初期以螺旋状态逐节伸展，如图5所示.

图5 盘绕式伸展臂以螺旋状态逐节伸展

为得到横杆刚度对伸展臂展开过程的影响，以表1所示盘绕式伸展臂为准，取横杆半径为0.5 mm，0.6 mm，0.65 mm，0.7 mm，按图5 所示进行展开过程仿真计算.其中顶板伸展速度为1mm/s.在第2层横杆处发生“snap through”现象时，截取伸展臂的变形状态进行比较.

图6a～图6c的第1幅图都是在第2层横杆弯曲程度最大时的状态.由图6可以得到以下结论.

1)第2层横杆发生“snap through”现象后，盘绕式伸展臂开始以逐层展开模式伸展(横杆的弯曲状态反映了盘绕半径的变化).

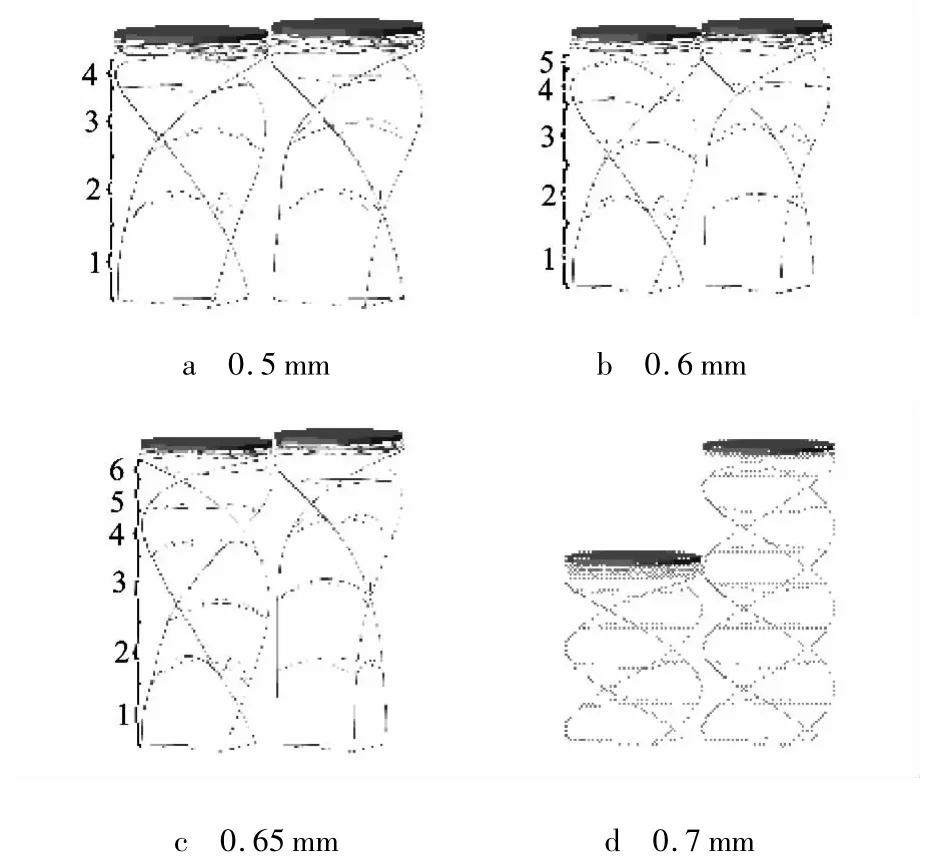
图6 不同横杆半径的盘绕式伸展臂展开

2)随着横杆半径的增加，第2层横杆发生“snap through”现象时伸展臂的长度逐渐增大.从半径为0.5mm的4节到0.65mm的6节.极端情况下纵杆无法伸直而逐级螺旋伸展(图6d).

3)当横杆半径足够大时，纵杆能量不足以压弯横杆，使得伸展臂以螺旋展开模式伸展(图6d).

考虑到盘绕式伸展臂以中心绳索控制方式展开时，其收纳筒一般较短.当螺旋状态的节数较多时，会发生较大的晃动.因此在本文中只认为伸展臂发生“snap through”效应时，伸展节数为5节以下的情况为逐层展开，5节以上定义为螺旋展开.其中第n节纵杆开始伸展以第n层铰链和收拢段纵杆脱离接触为准，如图7所示.

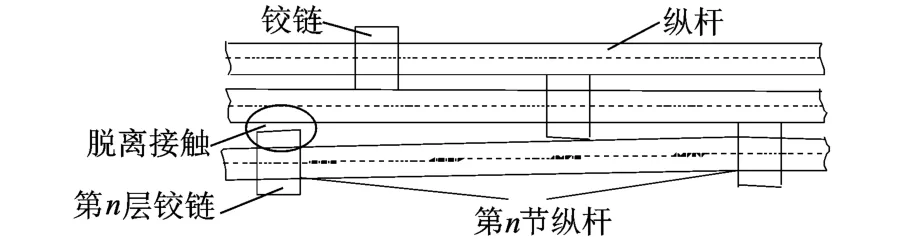
图7 第n节纵杆开始伸展

2.2 展开模式的判据

从上述分析可知:第2层横杆抗弯能力和纵杆对其压缩能力决定了盘绕式伸展臂的展开模式.若第2层横杆可以被压缩至两端距离为dmin，且此时展开节数小于5，伸展臂就可以逐层展开.

若盘绕式伸展臂缓慢伸展，则可以忽略动力学效应［10］.取第2层横杆张力最大时(两端距离为dmin)伸展臂的状态进行分析.设此时第2层横杆的张力为Fdm，用Fdm反映横杆的抗弯能力.

反映纵杆压缩能力的参数按下述方法定义:

1)调整横杆半径至某一个值rl，使得第2层横杆刚好可以弯曲至两端距离为dmin，且此时第6层铰链恰好与收拢段铰链脱离接触.定义此时盘绕式伸展臂的构型参数为临界参数.

2)定义在上述变形下，纵杆作用在第2层横杆上的压力为Fdl.用Fdl来表示纵杆的压缩能力.

3)Fdm＜Fdl，说明纵杆压缩能力较大，盘绕式伸展臂可以逐层展开

4)Fdm＞Fdl，说明横杆抗弯能力较大，盘绕式伸展臂无法逐层展开(包括形成逐层展开模式时伸展节数为6节的情况).

上述判据的前提条件为伸展臂缓慢伸展，为静力平衡.实际上在伸展臂展开过程中会有冲击、干扰等因素，因此会有一定误差.

2.3 判据的验证

与2.1节相同，用图4所示ST8伸展臂模型进行仿真计算.调整横杆半径约为0.63 mm，此时伸展臂可以形成逐层展开模式，且满足上节临界参数定义.观察第2层横杆受力与距离变化曲线，以及第2层横杆发生“snap through”前后的变形如图8所示(压力的负值表示横杆受拉).

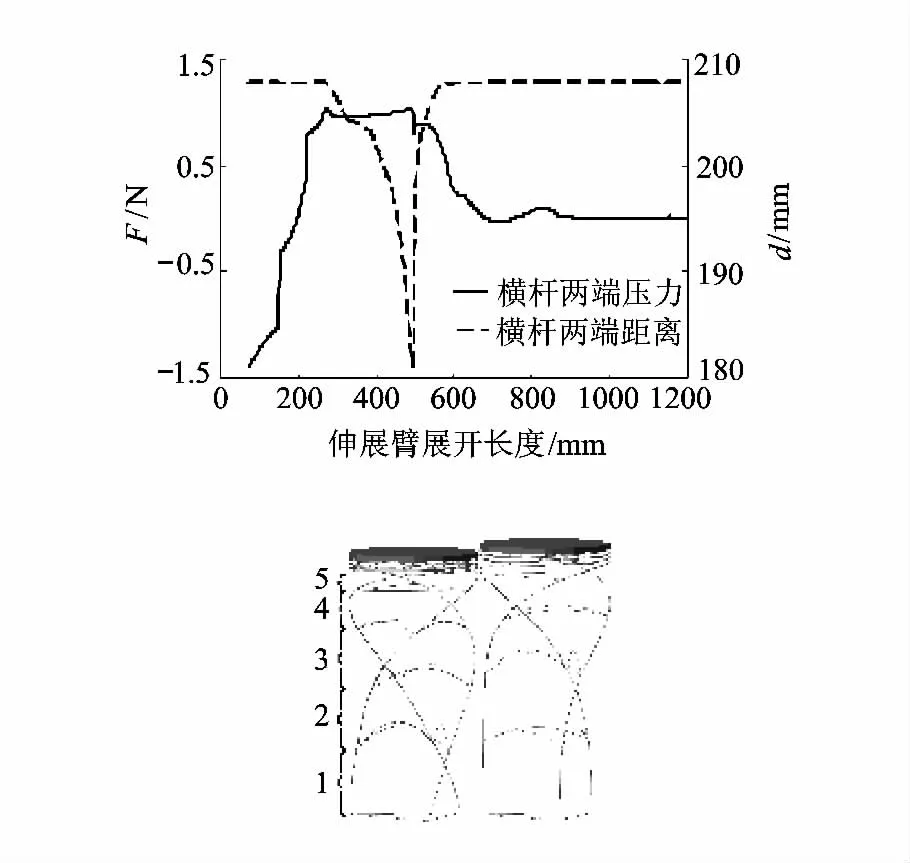
图8 临界参数下横杆受压及伸展臂snap through变形

当两端距离最小时(虚线)，横杆所受压力即为Fdm.由于伸展臂缓慢展开，可以认为横杆弯曲最大时处于平衡状态.因此取临界参数(图8)的Fdm为Fdl.由图8得到Fdl约为1.04 N.

另外分别研究横杆半径为0.62mm，0.64mm时的情况，得到仿真结果见图9.

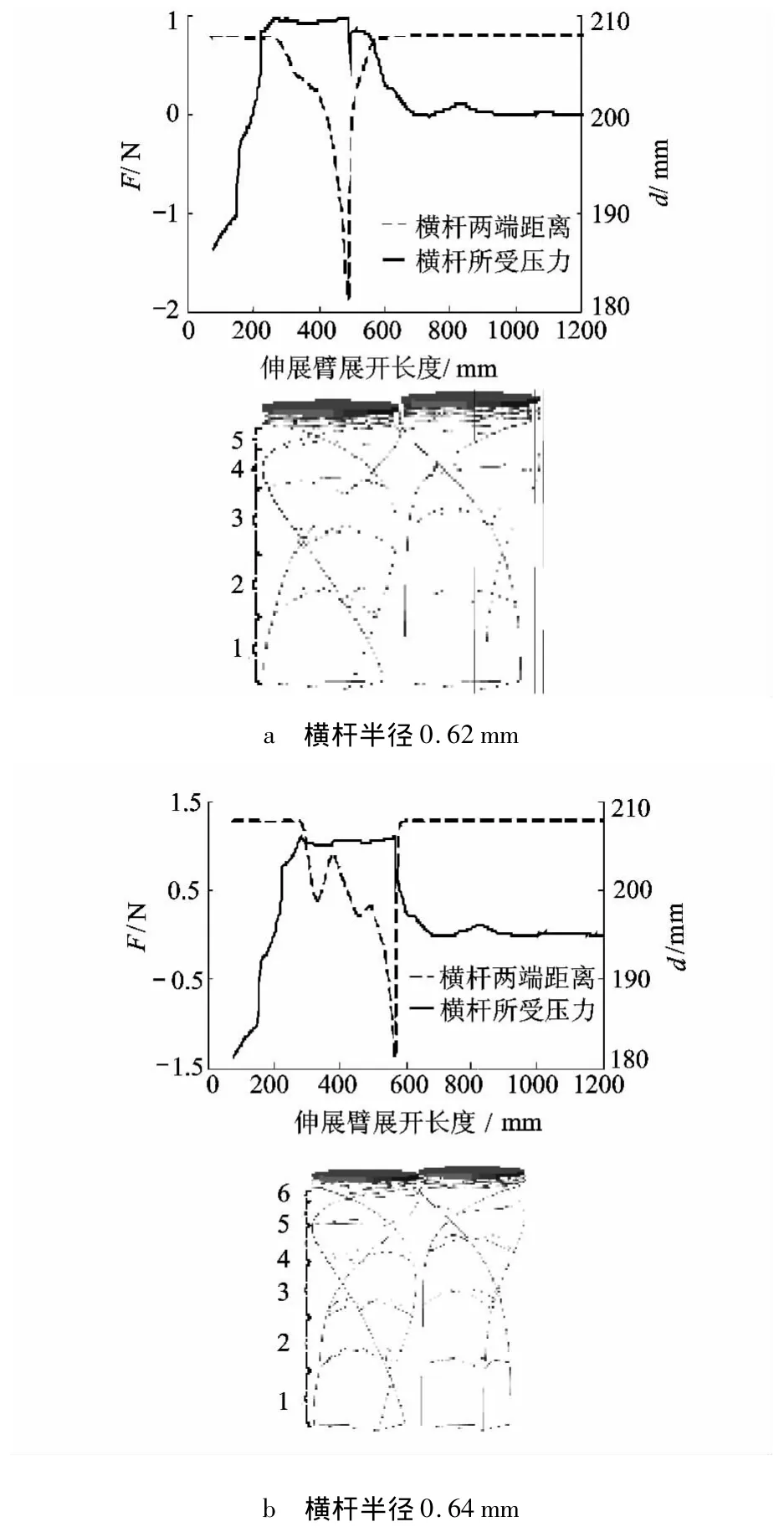
图9 第2层横杆受压及伸展臂snap through变形

图9a得到横杆半径为0.62 mm时，Fdm约等于0.97 N;图9b得到横杆半径为0.64 mm时，Fdm约等于1.11 N.即

横杆半径为0.64 mm:Fdm＞Fdl，纵杆在发生snap through现象时已有6层开始伸展;

横杆半径为0.62 mm:Fdm＜Fdl，纵杆在发生snap through现象时展开层数为5层.

仿真结果说明了判据的正确性，但判据所需要的Fdm，Fdl不能直接得到.下文研究利用伸展臂设计参数推导Fdm，Fdl，从而得到展开模式.

3 判据参数的求解

3.1 Fdm求解

横杆端部与铰链连接如图10所示，在受压时会发生类似于平面简支梁的变形.

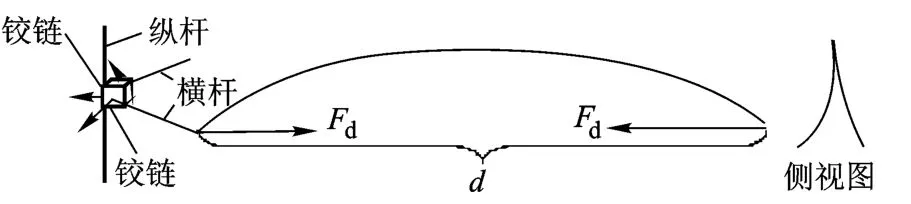
图10 横杆端部连接及变形

文献［14］利用弹性细杆的Kirchhoff动力学给出了简支梁两端受压情况下压力与距离的公式:

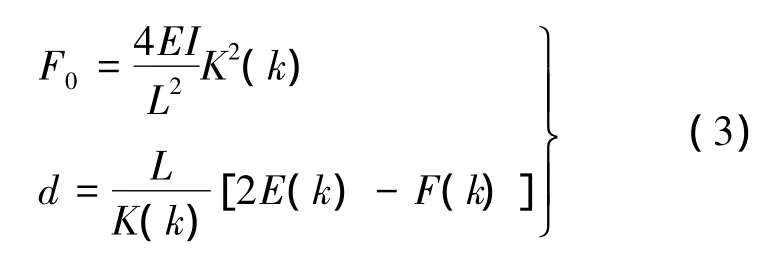
式中，EI为横杆弯曲刚度;L为横杆长度.k为随压杆弯曲程度增大而变大的量;K(k)，E(k)，F(k)为关于 k的椭圆积分［14］.

根据图4所示ST8伸展臂模型(横杆半径为0.5 mm)的仿真结果，取横杆两端压力及距离，与式(3)对比见图11.

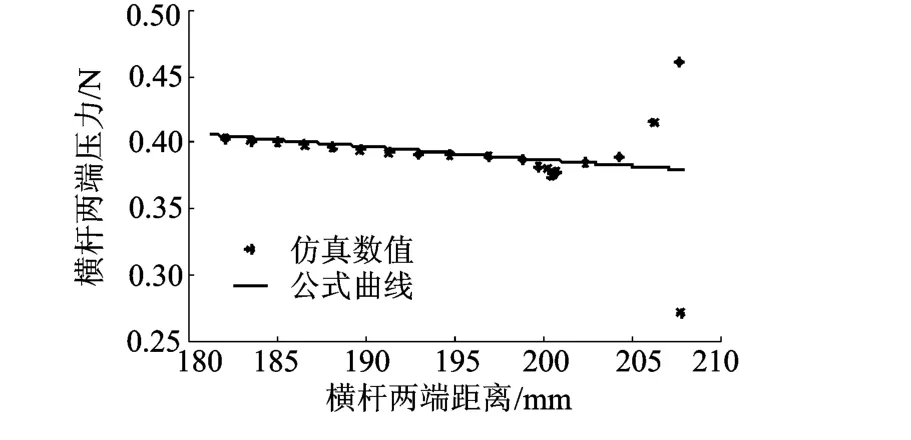
图11 横杆受压及两端距离变化

横杆原长207.8 mm，由图中可见，横杆变形较小时，仿真结果和式(3)有较大差别.但变形较大时，二者较为吻合.因此，可以用式(3)近似反映Fdm.

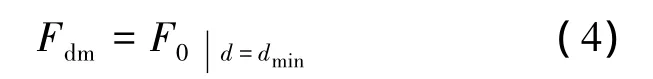
3.2 Fdl求解

Fdl是纵杆展开5节且第2层横杆弯曲至两端距离为dmin的条件下，纵杆对第2层横杆的压力.假设此时纵杆变形如下:

1)纵杆的第1，2节保持纯螺旋状态(螺旋角不变)，螺旋角为θmin(图3);

2)从第3节开始，经过3节纵杆，螺旋角逐渐增大到收拢段(接近90°).

在图8所示伸展臂发生“snap through”现象时，将纵杆在圆柱面上投影可描述纵杆变形.与上述定义的纵杆变形进行比较，如图12所示.

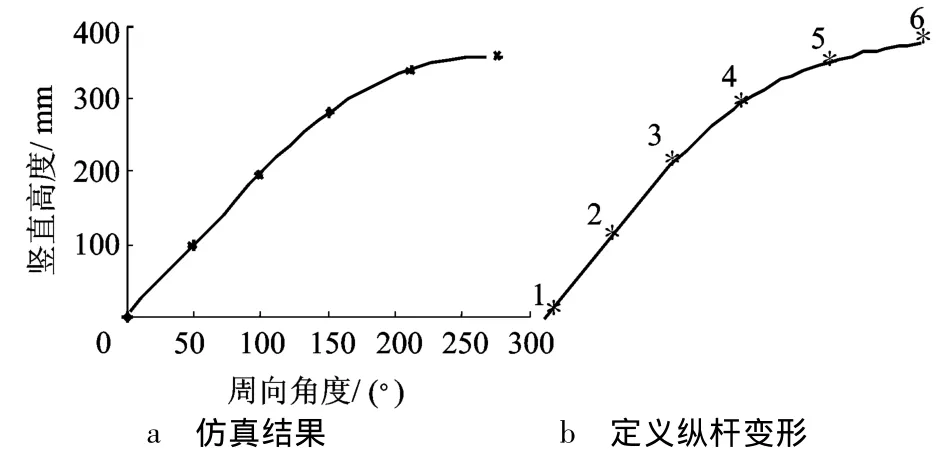
图12 纵杆变形

由图12可知，假设的纵杆变形较为合理.以此假设纵杆变形为前提，分析纵杆对横杆的压力.

盘绕半径在伸展时会减小，但变化幅值相对较小，图3盘绕半径最大变化约7%.因此可以认为纵杆沿圆柱面发生变形，圆柱面半径为R0.

3.2.1 上层纵杆变形分析

图12b所示纵杆，上层3～5节与1，2节变形不同，其螺旋角是连续变化的.对3～5节纵杆应用圆柱面约束假设，根据弹性细杆的Kirchhoff动力学理论，满足下述平衡方程［14］.

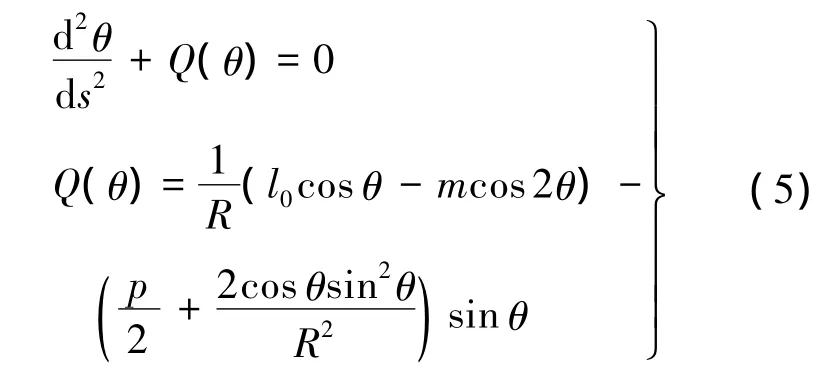
式中，θ为纵杆某一截面处的螺旋角;s为纵杆弧坐标;p，l0，m 是与纵杆受力有关的量［14］.其中，p与纵杆竖直方向压力Fz成正比，m与纵杆扭转变形相关，l0与纵杆所受竖直方向上扭矩成正比.

利用式(5)求解图12b中第3～5节纵杆螺旋角的变化.积分初值为第5节纵杆顶端的螺旋角及其变化率:θ0=89°，dθ0=0.

调整Fz大小，使得第3节纵杆下端的螺旋角为θmin.即在确定纵杆变形的条件下可以得到纵杆所受竖直方向压力Fz，且Fz沿纵杆不变［14］.

3.2.2 螺旋段纵杆

图12所示第1，2节纵杆的螺旋角恒定为θmin.第2层横杆受两节纵杆对应的斜拉索作用，对铰链进行受力分析如图13所示.

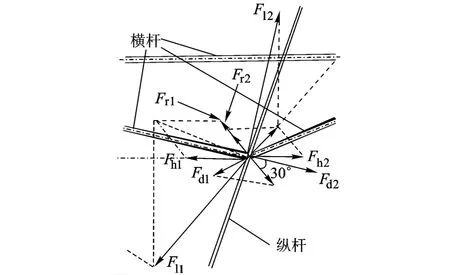
图13 第2层横杆受力分析

图13中Fl为斜拉索拉力，沿竖直、径向、周向分解为Fr，Fh，Fv.Fd为横杆对铰链的张力.

由于第1，2节均为纯螺旋杆，因此式(5)中 Q(θ)=0［14］.即

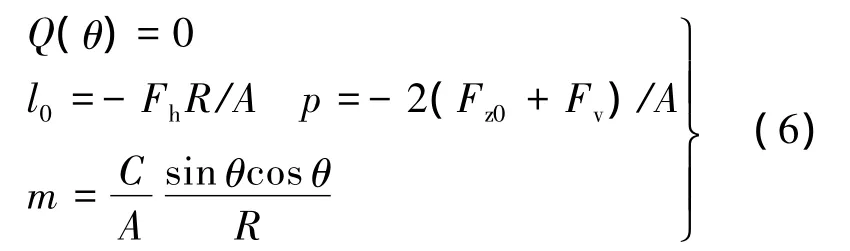
式中，θ取θmin;Fz0由3.2.1节上层纵杆变形计算得到;Fh，Fv均为斜拉索分力，可以通过几何条件得到.这样就可以得到Fh或Fv的值，从而得到斜拉索拉力沿径向的分量Frhelix.

图13中沿铰链径向受力平衡，因此可以得到

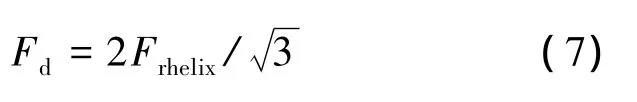
式(7)即为第2.2节判据所定义的Fdl.

4 盘绕式伸展臂构型与展开模式

根据图12定义的纵杆变形，采用第3节的方法，可以求得多组构型参数对应的Fdl和Fdm.利用第2.2节的判据，就可以判断不同构型参数的盘绕式伸展臂对应的展开模式.

参照文献［15］取节距与盘绕半径比值t/R为横轴，纵、横杆刚度比值为纵轴，列出盘绕式伸展臂展开模式与构型参数的关系，如图14所示.其中点 D，C，E分别对应图8，图9a，图9b的情况.ST8点为ST8伸展臂，可逐层展开.

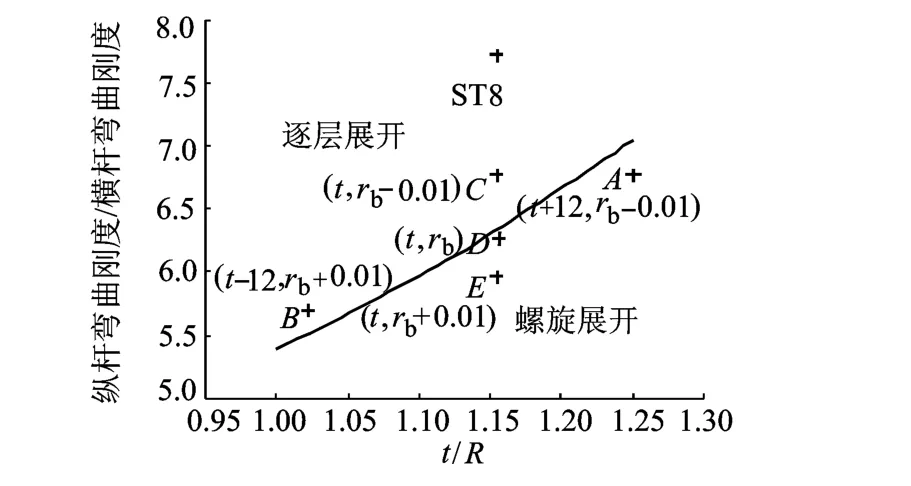
图14 盘绕式伸展臂伸展模式图

图14坐标平面中的每个点代表一组伸展臂的构型参数，其中斜线对应在图12所定义纵杆变形情况下的临界参数(此时Fdm=Fdl)，斜线上方满足Fdm＜Fdl，斜线下方满足 Fdm＞Fdl.根据第2.2节判据，可以得到对应的展开模式.

选取图14中5个点，取第2层横杆处发生“snap through”现象前后伸展臂变形进行比较.

其中D点对应图8所示盘绕式伸展臂，较为靠近临界点.C，E对应图9a，图9b所示盘绕式伸展臂，在D点基础上改变横杆半径.

A点在C点基础上增大节距为150 mm.展开图形见图15a.和图9b相似，伸展臂虽然可以发生“snap through”效应形成逐层展开，但此时长度为6节，根据2.1节定义认为A点螺旋伸展.

B点在E点基础上减小节距为126 mm，伸展臂以逐层展开.展开图形见图15b，长度5节.

上述5个盘绕式伸展臂的仿真结果说明:

1)图14可以判断盘绕式伸展臂的展开模式.

2)通过增大纵、横杆刚度比或减小节距、盘绕半径比值，可以调整盘绕式伸展臂的展开模式.

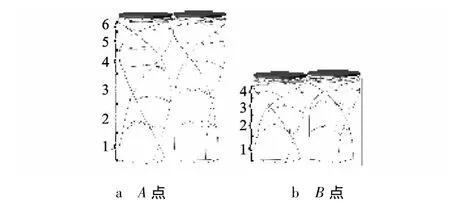
图15 伸展臂展开过程变形状态

5 结论

盘绕式伸展臂能否以逐层展开模式伸展，关键在于第2层横杆的变形.当作用在第2层横杆上的压力能使其弯曲到一个最大值时，会发生“snap through”效应而形成逐层展开模式.

横杆刚度越小，盘绕式伸展臂可以在展开节数越小的情况下形成逐层展开模式，反之展开节数越长.当横杆刚度足够大时，伸展臂最终只能形成整体的螺旋形状，而无法自行伸展.

考虑到实际盘绕式伸展臂展开过程中的冲击和干扰，图14与实际结果会有一定的误差.较稳妥的方法是选择离图14中斜线较远的点来设计伸展臂，在通过试验及仿真计算来调整参数，可以准确的控制伸展臂的展开模式.

References)

［1］于登云，杨建中.航天器机构技术［M］.北京:中国科学技术出版社，2011:94-104 Yu Dengyun，Yang Jianzhong.The spacecraft mechanism technology［M］.Beijing:China Science and Technique Press，2011:94-104(in Chinese)

［2］ McEachen M E.Validation of SAILMAST technology and modeling by ground testing of a full-scale flight article［C］//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Orlando，Florida:AIAA，2010

［3］ Murphy D M.Deployment demonstration and validation of SABUR:a stable articulating backbone for ultra-long radar［C］//AIAA SPACE 2007 Conference＆ Exposition.Long Beach，California:AIAA，2007

［4］陈务军，张淑杰.空间可展结构体系与分析导论［M］.北京:中国宇航出版社，2006:25-34 Chen Wujun，Zhang Shujie.Deployable space structures and analysis theory［M］.Beijing:China Astronautic Publishing House，2006:25-34(in Chinese)

［5］ McEachen M E，Trautt T A.Confirmation of new analytics for ultra-light lattice column strength using a 40-m flight article［C］//50th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics＆ Materials Conference.Palm Springs，California:AIAA，2009

［6］ Eiden M，Brunner O，Stavrinidis C.Deployment analysis of olympus astromast and comparison with test measurements［J］.Journal of Spacecraft and Rockets，1987，24(1):62-68

［7］ Natori M，Okazaki K，Sakamaki M，et al.Model study of simplex masts［C］//15th Internatiional Symposium on Space Technology Science.Tokyo:［s.n.］，1980

［8］ Seemann W.Deformation of an elastic helix in contact with a rigid cylinder［J］.Archive of Applied Mechanics，1996，67(1/2):117-139

［9］ Van der Heijden G H M，Champneys A R，Thompson J M T.Spatially complex localization in twisted elastic rods constrained to a cylinder［J］.International Journal of Solids and Structures，2002，39(7):1863-1883

［10］刘延柱，薛纭.弹性杆盘绕折叠的力学分析［J］.力学季刊，2008，29(3):343-348 Liu Yanzhu，Xue Yun.Mechanical analysis of coiling process of an elastic rod ［J］.Chinese Quarterly ofMechanics，2008，29(3):343-348(in Chinese)

［11］刘延柱，薛纭.受圆柱面的螺旋杆伸展为直杆的动力学分析［J］.力学学报，2011，43(6):1151-1156 Liu Yanzhu，Xue Yun.Dynamical analysis of stretching process of helical rod to straight rod under constraint of cylinder［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43(6):1151-1156(in Chinese)

［12］ Murphy D M，Macy B D.Demonstration of a 10-m solar sail system ［C］//45th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics ＆ Materials Conference.Palm Springs，California:AIAA，2004

［13］ Murphy D M，McEachen M E，Macy B D.Demonstration of a 20-m solar sail system［C］//46th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics ＆ Materials Conference.Austin，Texas:AIAA，2005

［14］刘延柱.弹性细杆的非线性力学——DNA力学模型的理论基础［M］.北京:清华大学出版社，2006 Liu Yanzhu.Nonlinear mechanics of thin elastic rod—theoretical basis of mechanical model of DNA［M］.Beijing:Tsinghua University Press，2006(in Chinese)

［15］ Kitamura T，Okazaki K，Natori M，et al.Development of a“HINGLESS MAST”and its applications［J］.Acta Astronautica，1988，17(3):341-346