基于全相FFT的多频比相测距方法研究

江晓东，谢京稳

(北京跟踪与通信技术研究所， 北京100094)

0 引言

连续波比相测距雷达通过测量不同频率信号之间的相位差来对目标距离进行测量，此种雷达具有结构简单、测距精度高、便于采用数字信号处理技术等优点［1］。连续波比相测距雷达一般采用快速傅里叶变换(FFT)求解相位差。然而，传统的FFT存在比较严重的频谱泄露效应，频谱泄漏会降低相位测量精度［2-3］。尤其是在多目标的情况下，信号的频谱泄露会对其他信号频谱的相位产生严重影响，降低相位估计精度，进而降低目标的测距精度。文献［4］提出一种全相位FFT谱分析方法，并指出全相FFT比传统FFT具有更优良的抑制频谱泄漏性能。本文用全相FFT代替传统的FFT来进行测量相位，并通过仿真验证了全相FFT可有效得抑制频谱泄露，从而提高此种雷达的测距精度。

1 比相测距原理

连续波比相测距的基本原理是双频比相测距，其原理如图1所示。

假设发射两个频率为f0、f1，频差为Δf的连续正弦波(f1=f0+Δf)。发射信号为S0(t)=cos(2πf0t+φ0)和S1(t)=cos(2πf1t+ φ1)，其中φ0和φ1为任意(常量)初相。回波信号由于多普勒效应产生频移。接收机将两个回波信号成分区分开来，并分别将各成分与相应的发射波形混频，取出两个多普勒频率成分x0(t)、x1(t)。发射的两个信号由于频率差产生了一个与目标距离有关的相位差。

图1 比相测距基本原理

FFT比相测距的一般流程如图2所示，首先对x0(t)、x1(t)进行采样，获取 x0(n)、x1(n)，再对其分别作FFT，接着进行谱峰搜索，获取谱峰谱线的位置序号k0、k1，再根据各自谱峰的实虚部求出相位φ0(k0)、φ1(k1)，以此作为各自对应信号的相位，然后求出两者的相位差Δφ，再根据此相位差与距离的关系式就可确定对应的目标距离R。

双频比相测距系统由于存在最大不模糊距离和测距精度的矛盾［5］，现实中一般采用多频测距来克服这一矛盾，常用的方法有“参差多频”“二次差频”等。本文采用“参差多频”法，其具体内容及解模糊方法见文献［5-6］。

图2 比相测距算法基本流程

2 全相FFT谱分析方法简述

全相位频谱分析详见文献［7］，其大致过程如图3所示。

图3 全相位FFT谱分析的基本框图(N=4)

传统FFT谱分析直接对采样数据截断后进行FFT即得谱分析结果，但一般情况下会导致较严重的频谱泄漏效应。而全相FFT谱分析如图3所示，即需用长为(2N-1)的卷积窗ωc对中心样点x(0)前后(2N-1)个数据进行加权，然后将间隔为N的数据两两进行重叠相加，再对重叠相加后的N个数据进行FFT即得全相位谱分析结果。

图3中的卷积窗由前窗f与翻转的后窗b卷积而成［4］，即

当 f，b 为对称窗时，ωc(n)满足

若f=b=RN(RN为矩形窗)，则称为无窗全相位频谱分析;若f，b中其一为RN，则称单窗全相位频谱分析;若f=b≠RN则称为双窗全相位频谱分析。这里只讨论无窗的情况。

全相FFT谱分析方法如下:首先用长为(2N-1)的卷积窗ωc对中心样点x(0)前后(2N-1)个数据进行加权，然后将间隔为N的数据两两进行重叠相加，再对重叠相加后的N个数据进行FFT即得全相位谱分析结果。由可见FFT和全相FFT之间惟一的差别是对截断数据预处理的方式不同［8］。

文献［7］证明了全相FFT的两个重要性质:

1)长度为(2N-1)的复指数序列经过N阶无窗全相位FFT谱分析后，其主谱线上的相位谱值等于输入序列的中心样点相位的理论值，与信号的频率偏差值无关。即全相位FFT谱分析具有“相位不变性质”。

2)序列{x(n)=ej(ω0n+θ0)，-N+1≤n≤N-1}归一化后的全相位FFT振幅谱与传统FFT振幅谱存在平方关系。

性质2是全相FFT谱分析的一个重要性质，它所揭示的平方关系是对所有N条谱线而言的，这就使得旁谱线相对于主谱线幅度的比例也按平方关系而减小，从而使主谱更为突出，继而获得很好的抑制频谱泄漏性能。

3 基于全相FFT法的比相测距系统

本文提出利用全相FFT代替传统FFT，这就构成基于全相FFT的比相测距系统，其一般计算流程如图4所示。

图4 基于全相FFT的比相测距算法流程

全相FFT的输入数据为2N-1个数据{x(n)=ej(ω0n+θ0)，0≤n≤(2N-1)}其相位差与距离的转换公式如下

式中:Δf=f1-f0;Δφ为两个多普勒信号谱峰的相位差。

由式(3)可知:在目标作径向匀速直线运动的情况下，经全相FFT处理所得的两个多普勒信号谱峰相位之差Δφ按式(3)计算所得的距离表示的是t0+(N-1)Δt时刻的目标距离，即所对应采样时间段中间时刻点的距离。

需要说明的是，式(3)是在目标作径向匀速直线运动的条件下推导出来的，文献［9-10］则给出了目标一般运动时的距离与相差的理论表达式，证明了目标在作一般运动时，其多普勒频率不再是作径向匀速直线运动时的常数，而是时变函数。然而这一公式需要首先求出目标的瞬时速度和加速度，这两个量往往本身就是未知的，所以这一公式还无法直接运用到工程实践中。但是，目标在作一般运动时，只要其径向加速度不大，在很短的采样间里，其多普勒频率变化不大，仍然可以利用式(3)求解目标距离。

4 仿真结果

为验证全相FFT在多目标下抑制频谱泄露的性能，对多目标作径向匀速直线运动情况进行计算机仿真。

1)仿真条件:

目标参数:设雷达波束范围内共有4个目标，其速度分别为 100 m/s ，230 m/s，260 m/s，400 m/s(远离雷达为负，否则为正);目标初始距离均为10 km;雷达回波幅度均为常数1，不随目标距离改变。

雷达参数:雷达基准频率f0=10.5 GHz，基本频差5.4 MHz，参差重数取3，参差系数为(7，8，9)。采样频率125 kHz。FFT点数为1 024，每隔1 024个采样点计算1次距离，共计算1 000点。

2)仿真结果:

(1)波束范围内单目标

设在测量时段，速度为100 m/s，230 m/s，260 m/s，400 m/s的四个目标回波依次出现在雷达波束范围内，互不影响，且回波信号没有受到噪声干扰，即信噪比为无穷大。雷达对单目标进行距离测量，则对4个目标的测距精度如图5所示。

图5 无噪单目标情况下的测距精度

由图5可知，传统FFT和全相FFT比相后解得的距离与理论上的理想距离(采样时间段中间点所对应目标距离)之间绝对误差均小于10-7m，所以在无噪声且雷达波束内只有单目标的情况下，FFT和全相FFT均可准确得测得目标距离，这也证明了式(3)的正确性。

(2)波束范围内多目标

设在测量时段，速度为100 m/s ，230 m/s，260 m/s，400 m/s的4个目标回波同时出现在雷达波束范围内，且没有受到噪声干扰，即信噪比为无穷大。雷达对多个目标同时进行距离测量，则对4个目标的测距精度如对图6所示。

将图6与图5对比可知，在无噪多目标的情况下，不论是采用传统FFT，还是采用全相FFT，4个目标的测距精度都严重下降。这是由于各个信号的频谱泄露互相影响，降低了相位测量精度，从而降低了测距精度。

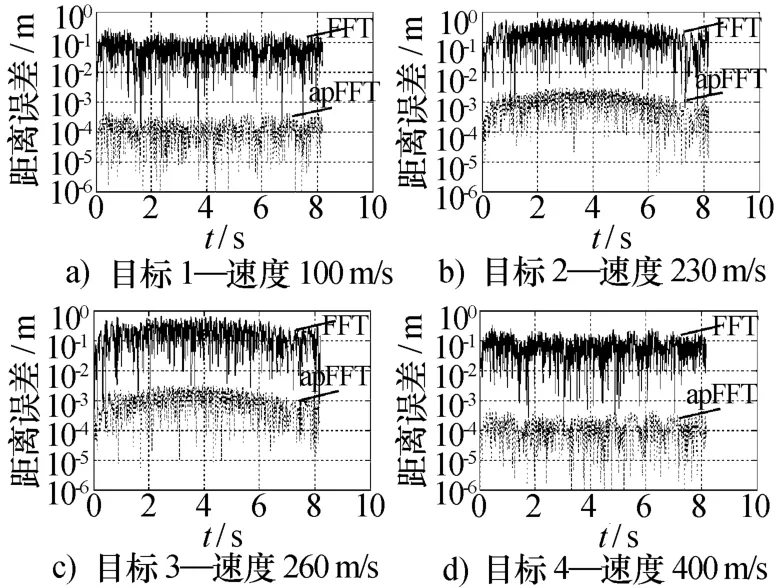
图6 无噪多目标情况下的测距精度

对于FFT法来说，4个目标的测距精度均由约10-7m降低到10-1m，整整降低了6个数量级，由此可见在无噪多目标的情况下，当采用FFT比相测距时，频谱泄露对相位测量的影响是十分严重的。这极大地降低了此种雷达的多目标情况下的测距精度，故必须采用一些抑制频谱泄露的方法。

对于全相FFT来说，由于具有较好的频谱泄露能力，相比于传统FFT，频谱泄露造成影响较弱。对于目标1和4来说，由于速度与其他目标速度相差较远，故多普勒频率相差较远，所以受到其他多普勒信号频谱泄露的影响较轻，故其测距精度相对于无噪单目标情况下测距精度只降低了约4个数量级，优于10-3m，远远高于传统FFT在此种情况下10-1m的测距精度;而对于目标2和目标3来说，由于彼此的频率间隔较近，频谱泄露较为严重，其测距精度相对于无噪单目标情况下测距精度约降低了5个数量级，但依然优于10-2m，仍高于传统FFT在此种情况下10-1m的测距精度。

(3)波束范围内多目标，信噪比为40 dB，蒙特卡洛仿真200次

设在测量时段，速度为100 m/s ，230 m/s，260 m/s，400 m/s的4个目标回波一同出现在雷达波束范围内，同时回波受到噪声干扰，信噪比为40 dB。雷达对多个目标同时进行距离测量，则对4个目标的测距精度如图7所示。

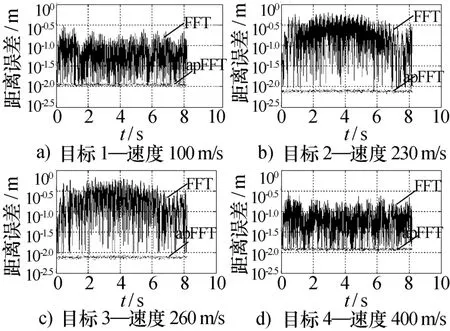
图7 有噪多目标情况下的测距精度

对比图6与图7可知，在有噪声的情况下，由于回波信号受到噪声干扰，不论是采用FFT，还是采用全相FFT，测距精度均下降，但是全相FFT的测距精度，仍然要比FFT高出一个数量级，可见即使是在有噪多目标的情况下，全相FFT也要比FFT有着更高的测距精度。

综上可知，若雷达波束内同时出现多目标，由于不可避免的频谱泄露，会极大地降低多频比相测距雷达的测距精度。在此种情况下，全相FFT相比于传统FFT，能够较好的抑制了频谱泄露，从而极大地提高了多频比相测距雷达在多目标情况下的测距精度。

5 结束语

在多频连续波比相测距雷达中，本文利用全相FFT代替了传统FFT，通过计算机仿真，证明了全相FFT比传统FFT有着更好得抑制频谱泄露的能力，提高了各频率分量的测相精度，进而有效提高了多频比相测距雷达在多目标情况下测距精度。

［1］许邦建，王 展，皇甫堪.FFT比相测距雷达中的相差—距离关系研究［J］.兵工学报，2001，22(1):53-56.Xu Bangjian，Wang Zhan，Huang Fukan.Relationship between phase difference and range in FFT phase-comparing ranging radars［J］.Acta Armamentarii，2001，22(1):53-56.

［2］Xie Ming，Ding Kang.Correction for the frequency amplitude and phase in FFT of harmonic signal［J］.Mechanical System and Signal Processing，1996，10(2):211-221.

［3］Dusan Agrez.Improving phase estimation with leakage minimization［J］.IEEE Transactions on Instrumentation and Measurement，2005，54(4):1347-1353.

［4］王兆华，黄翔东.数字信号全相位谱分析与滤波技术［M］.北京:电子工业出版社，2009.Wang Zhaohua，Huang Xiangdong.Digital signal all-phase spectrum analysis and filtering technology［M］.Beijing:Publishing House of Electronics Industry，2009.

［5］曹延伟.多频连续波雷达跟踪控制器设计及相关理论和算法研究［D］.长沙:国防科技大学，2005.Cao Yanwei.Design of tracking controller of multiple frequency CW radar and research on related theory and algorithm［D］.Changsha:National University of Defense Technology，2005.

［6］许邦建，李 纲，皇甫堪.测距雷达解距离模糊的两种快速算法［J］.电子与信息学报，2001，23(9):905-911.Xu Bangjian，Li Gang，Huang Fukan.Two fast algorithms of deambiguous technique in ranging radar［J］.Journal of Electronics and Information Technology，2001，23(9):905-911.

［7］黄翔东.全相位数字信号处理［D］.天津:天津大学，2006.Hua Xiangdong.All-phase digital signal processing［D］.Tianjin:Tianjin University，2006.

［8］王兆华，黄翔东.基于全相位谱分析的相位测量原理及其应用［J］.数据采集与处理，2009，24(6):777-782.Wang Zhaohua，Huang Xiangdong.Principle of phase measurement and its application based on all-phase spectral analysis［J］.Journal of Data Acquisition and Processing，2009，24(6):777-782.

［9］袁俊泉.皇甫堪.机动目标情况下FFT比相测距方法研究［J］.现代雷达，2005，27(9):14-17.Yuan Junquan，Huang Fukan.A study on ranging method based on FFT phase comparison for maneuvering target［J］.Modern Radar，2005，27(9):14-17.

［10］Yasotharan A，Thayaparan T.The performance of the fourier method in detecting an accelerating target and estimating its median velocity［C］//IEEE International Radar Conference(Section II).［S.l.］:IEEE Press，2000:59-64.