全容式LNG储罐在外爆炸荷载作用下的计算分析
宋延杰,李金光,郑建华
(中国寰球工程公司,北京 100012)
0 引言
根据参考文献 [1]的规定,LNG储罐设计时应考虑爆炸荷载对储罐的冲击作用。爆炸时产生的爆炸波是瞬间形成的高温高压气流,它从爆心以超音速向四面八方传播,作用时间只有几秒钟,当它到达储罐时,会使空气压强突然升高形成超压,并迫使空气迅速流动形成动压。由于实际工程中还没有出现过LNG储罐遭受爆炸荷载作用而破坏的实例,所以国内外对LNG储罐的爆炸荷载作用分析还仅仅处于理论研究阶段,本文采用ABAQUS软件对16万m3LNG储罐在爆炸荷载作用下的效应进行了数值模拟分析。
1 爆炸荷载特性
1.1 爆炸荷载的选取
根据国外工程的计算经验,一般采用以下两种形式的等效爆炸荷载来对LNG储罐进行计算:
(1)峰值入射超压:Ps0=32.5 kPa;作用时间:t=40 ms。
(2)峰值入射超压:Ps0=9.5 kPa;作用时间:t=85 ms。
上述两种爆炸荷载的形状都是右三角形,瞬间达到峰值,然后线性减小到零,如图1所示。
[2]和 [3]给出了波速U(m/s)的计算公式:

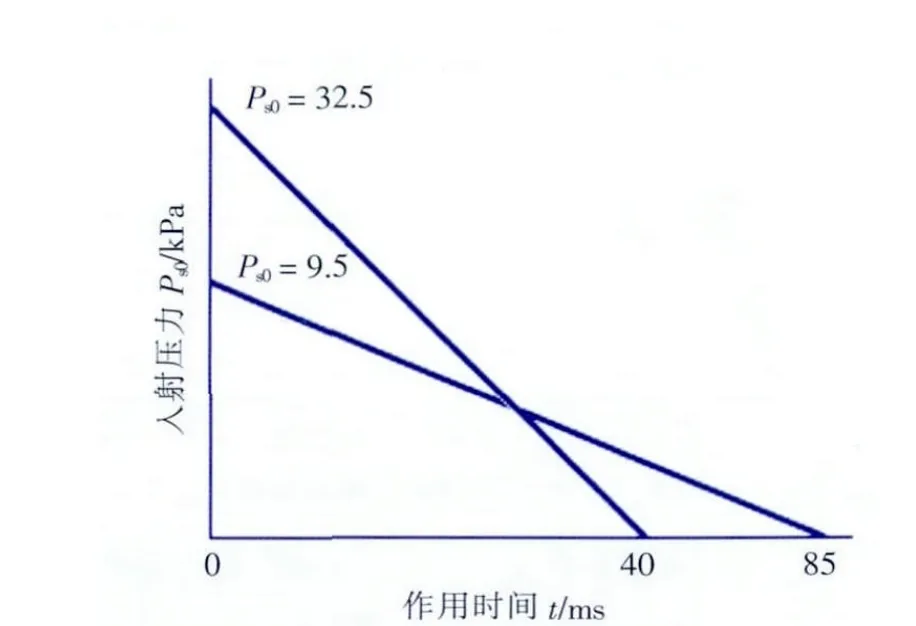
图1 爆炸荷载时程曲线
由公式 (1)计算可得,当Ps0=32.5 kPa时,U=389 m/s; 当 Ps0=9.5 kPa时, U=358 m/s。
1.2 反射压力分布曲线
当自由空间中的爆炸波撞击到物体的表面时,爆炸波会被反射,因此该表面将遭受一个比入射压力值更大的压力。反射压力值Pr_a既与峰值入射超压Ps0有关,也与爆炸波和作用面夹角α有关,该反射压力值可通过下面的公式得出:

式中,Cr_α是爆炸波与作用面成α夹角时的反射系数。参考文献 [2]和 [3]给出了α=0时的反射系数计算公式:

对于圆柱形罐壁,可由参考文献 [2]得到不同夹角α下的Cr_α分布曲线,如图2所示。

图2 Cr_α 分布曲线
1.3 爆炸荷载沿储罐的传播过程
在不同的时刻,爆炸荷载沿储罐罐壁传播时的反射压力分布如图3~5所示。

图3 t0、t1时刻罐壁反射压力分布
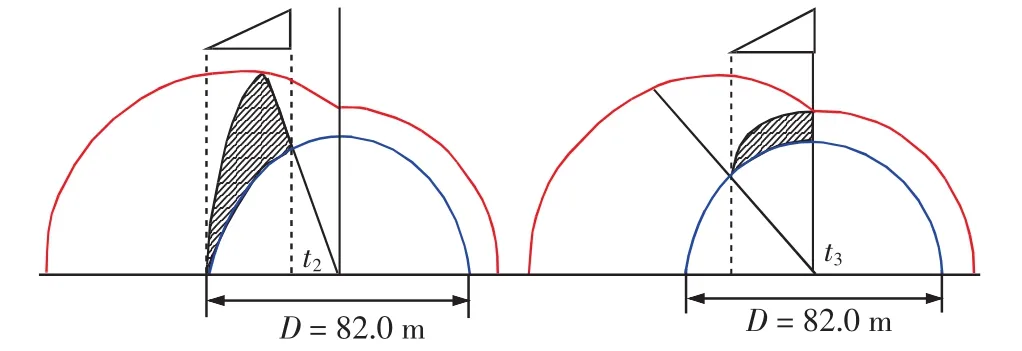
图4 t2、t3时刻罐壁反射压力分布
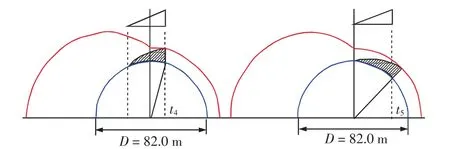
图5 t4、t5时刻罐壁反射压力分布
在不同的时刻,爆炸荷载沿储罐罐顶传播时的反射压力分布如图6所示。
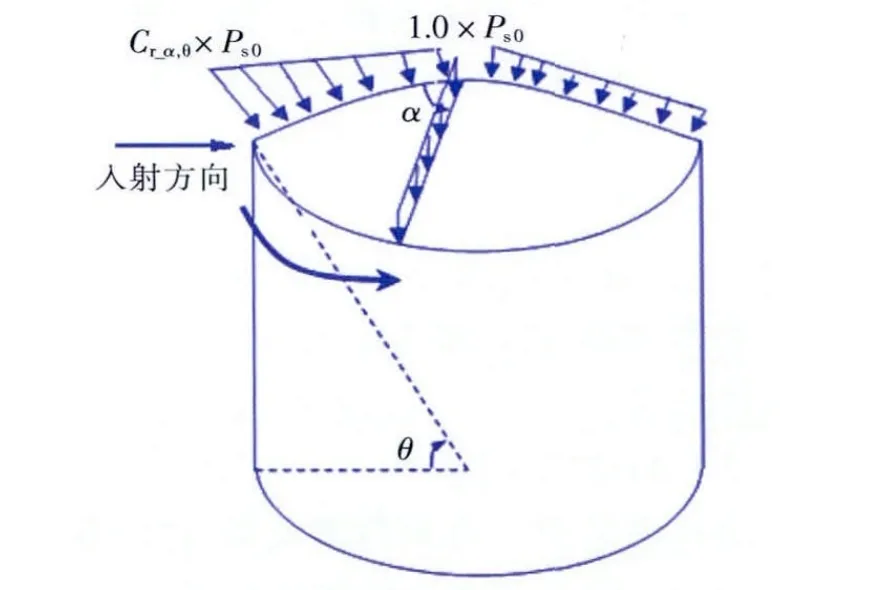
图6 不同时刻罐顶反射压力分布
2 动力分析要点
2.1 荷载简化
内罐罐壁和弹性毯自重简化为集中荷载施加到底板上;珍珠岩保冷层、内罐底板和附于底板上的材料 (保温材料、混凝土)自重简化为面荷载施加到底板上;抗压环、钢罐顶、吊顶及吊顶保温材料自重简化为集中荷载施加到罐壁上。
2.2 罐内液体简化
当LNG储罐受到爆炸荷载作用时,一部分液体与内罐罐壁刚性联系在一起运动,相当于实体接触,划分为冲击部分;另一部分液体则柔性地与罐壁接触,在罐内晃动,划分为晃动部分。在进行全容式LNG储罐爆炸荷载作用下的计算分析时,罐内液体质量和刚度均可简化为晃动部分和冲击部分,其数值大小可根据参考文献[4]计算得到。
2.3 爆炸作用计算步骤
全容式LNG储罐的爆炸作用计算分两步进行:
第一步为模态分析,计算得到储罐在盛满液体状态时对结构反应有显著贡献的前两阶圆频率。
第二步为爆炸作用分析,根据第一步得到的前两阶圆频率,计算出经典Rayleigh阻尼矩阵的质量比例系数α和刚度比例系数β;然后对罐体单元施加不同时刻的爆炸荷载进行动力时程分析,得到储罐在爆炸作用下的动力效应。
3 计算实例
3.1 基本参数
某16万m3全容式LNG储罐基本几何参数见图7。
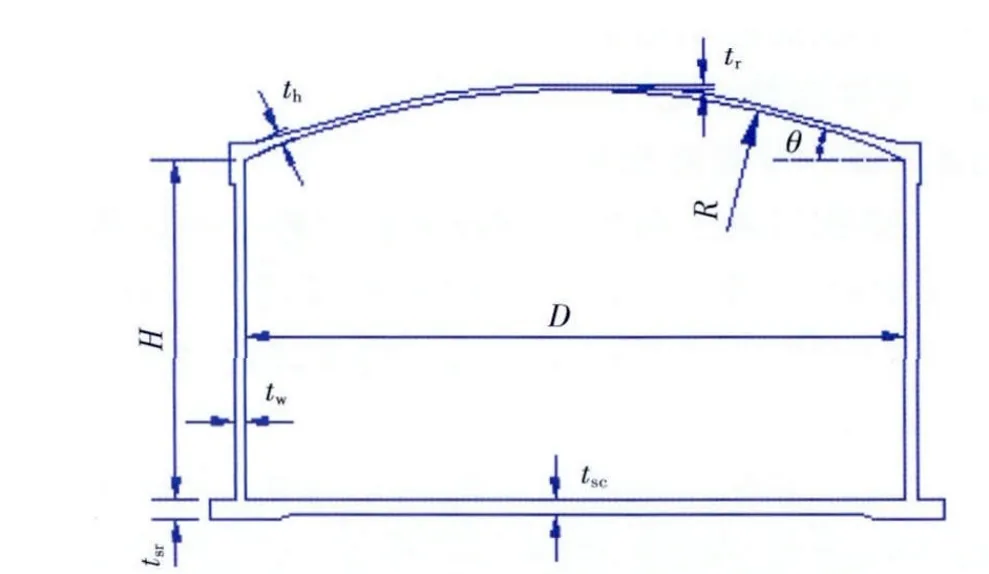
图7 全容式LNG储罐基本几何参数
外罐内直径D=82 m,罐壁高度H=38.55 m,壁厚tw=0.8 m,罐顶厚度中心tr=0.4 m,罐顶腋部厚度th=0.8 m,罐顶半径R=82 m,底板中心厚度tsc=0.9 m,底板边缘厚度tsr=1.2 m;C50混凝土,其密度ρc=2 500 kg/m3;内罐泄漏后的液位HL=33.3 m,液体密度ρL=480 kg/m3;考虑土体对地面以下桩的水平约束Kx=Kz=1.61×108N/m,竖向约束Ky=1.28×109N/m,抗弯约束Kxz=Kzx=4.67×108N·m/rad。
3.2 有限元模型
全容式LNG储罐的爆炸作用计算采用ABAQUS 6.7-3版软件。由于结构和边界条件的对称性,取一半实体模型来进行网格划分,计算模型如图8所示。其中,外罐部分的节点数为30 982,单元数为32 709,单元类型采用壳单元S4和S3;桩的节点数为1 800,单元数为1 620,单元类型采用梁单元B31;根据参考文献 [4],内罐液体部分简化为两个质点,通过弹簧弹性连接于底板中心;当罐内盛满液体时,冲击部分液体质量mi=2.027×107kg,水平刚度ki=3.513×109N/m,晃动部分液体质量mc=2.044×107kg,水平刚度kc=8.57×106N/m。
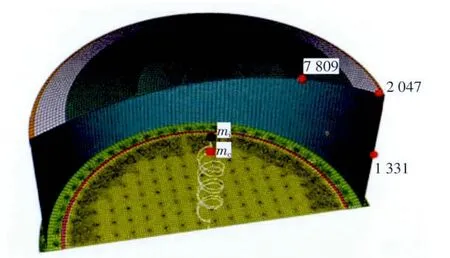
图8 选取的节点位置
3.3 阻尼参数计算
假设两个振型ωi和ωj具有相同的阻尼比ξ,则经典Rayleigh阻尼的质量矩阵和刚度矩阵的系数计算公式分别为[5]:

通过模态分析,得到对储罐反应有显著贡献的前两阶圆频率为 ωi=10.687 Hz和 ωj=23.489 Hz,当ξ=0.05时,由公式 (4)和 (5)计算得到:α =0.734 5, β=0.002 93。
根据参考文献[4]可以计算得到内罐冲击部分液体周期Ti=0.477 1 s,晃动部分液体周期Tc=9.70s。
因此,冲击部分液体的阻尼系数ξi取0.05时,其质量比例系数为:

晃动部分液体的阻尼系数ξc取0.005时,其质量比例系数为:
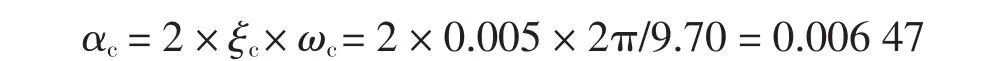
3.4 计算结果
3.4.1 结构变形
在爆炸荷载作用下,LNG储罐随时间变化的结构变形如图9~11所示。

图9 t=0.01 s时刻的结构变形/m

图10 t=0.1 s时刻的结构变形/m

图11 t=0.2 s时刻的结构变形/m
在峰值入射超压Ps0=32.5 kPa和Ps0=9.5 kPa的爆炸荷载作用下,LNG储罐在不同作用时刻的结构变形形状相似,但数值不同。
3.4.2 轴力—弯矩分布
为了对爆炸效应进行直观的对比分析,选取了罐壁节点号1 331、罐顶节点号2 047和7 809作为对比分析的数据点,具体位置见图8。此三节点在两种不同爆炸荷载作用下不同时刻的轴力—弯矩分布如图12~17所示。

图12 节点1 331在不同时刻的环向轴力—弯矩分布

图13 节点1 331在不同时刻的竖向轴力—弯矩分布

图14 节点2 047在不同时刻的径向轴力—弯矩分布
4 结果分析
(1)从图12~17的爆炸作用计算结果可以看出,峰值入射超压为Ps0=32.5 kPa的爆炸荷载对储罐的作用效应较Ps0=9.5 kPa的大。因此,在对全容式LNG储罐进行爆炸荷载作用分析时,应该选用Ps0=32.5 kPa的爆炸荷载。
(2)在爆炸荷载作用下产生的罐壁环向和竖向最不利作用效应在一、三象限拉力、正弯矩和压力、负弯矩呈对称分布,且轴力很大、弯矩较大。
(3)罐顶肋部径向轴力弯矩点主要分布在二、四象限 (拉力、负弯矩和压力、正弯矩),且轴力较小、弯矩很大;环向轴力弯矩点主要分布在一、三象限 (拉力、正弯矩和压力、负弯矩),且轴力很大、弯矩较小。
(4)罐顶中部径向轴力弯矩点全象限分布,且轴力较小、弯矩很小;环向轴力弯矩点全象限分布,且轴力很大、弯矩很小。
(5)储罐在爆炸荷载作用下,罐壁和罐顶在环向的作用效应较竖向和径向显著,且主要表现为使截面受拉,这对混凝土结构的受力非常不利,会引起截面配筋量的大幅度增加。

图15 节点2 047在不同时刻的环向轴力—弯矩分布

图16 节点7 809在不同时刻的径向轴力—弯矩分布
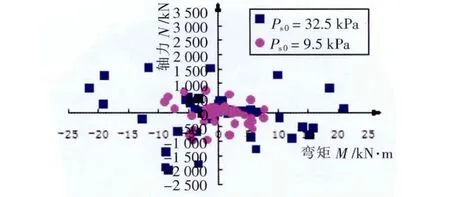
图17 节点7 809环向轴力—弯矩分布
参考文献:
[1]BS EN 14620-1:2006, Design and manufacture of site built,vertical, cylindrical, flat-bottomed steel tanks for the storage of refrigerated,liquefied gases with operating temperatures between 0℃ and-165℃ Party1:General[S].
[2]Task committee on blast resistant design.Design of Blast Resistant Buildings in Petrochemical Facilities [M].Reston,VA:ASCE Publications,1997.25-29.
[3]SH/T 3160-2009,石油化工控制室抗爆设计规范[S].
[4]郑建华,李金光,李艳辉.全容式LNG储罐的地震作用计算模型研究[J].化工设计,2012,22(2):11-14.
[5]乔普拉.结构动力学:理论及其在地震工程中的应用 (第二版)[M].谢礼立,吕大刚,译.北京:高等教育出版社,2007.341.

