PMD和PDL同时存在下偏振复用系统的ICA解复用

赵玲，胡贵军，吕金华，李公羽，李莉

（吉林大学 通信工程学院，吉林 长春130012）

1 引言

为了适应高速发展的信息化社会，通信系统在不断地追求更高的传输速率和更大的传输容量，这就使通信系统的扩容成为了一个亟待解决的问题。

偏振复用利用了光在单模光纤中传输的偏振特性，以同一波长的光在传输时产生的两个相互正交的偏振模作为两个独立信道，分别传输不同的信号。这种复用方式可以使现有的WDM系统容量和频谱利用率提高一倍[1,2]，且无需重新铺设线路，可以在已有系统的基础上实现快速、低成本的扩容升级。在偏振信号的传输过程中，由于光纤中存在双折射效应，导致了偏振模色散（PMD, polarization mode dispersion）的产生[3]。同时，系统中的连接器、耦合器等光器件中存在偏振相关损耗(PDL, polarization dependent loss)[4]。在偏振复用系统中，这2种效应会导致信号间的串扰，影响传输质量[5]。

针对偏振复用系统中PMD造成的串扰，现有的研究中多数采用相干检测，并应用数字信号处理（DSP, digital signal processing）对串扰进行消除，取得了很好的效果[6～9]。但是，系统中存在的 PDL会引发信号非酉变换，不仅造成偏振态之间正交性损失，同时还会使2个偏振支路之间的功率不均等，这使 2个各支路之间的串扰更加难以消除，所以PDL带来的影响成为了偏振复用系统中一个必须考虑的问题[10～13]。在实际系统中，PMD和PDL通常是同时存在的，且它们之间的相互作用十分复杂，对系统的综合影响难以具体计算，这种影响可以统一地归结为两路偏振信号间的相互串扰。而独立成分分析（ICA, independent component analysis）是一种盲估计算法，它的最大特点就是可以在混合过程未知的情况下，以信号间独立性为准则分离混合信号。由此可见，ICA算法对于 PMD和PDL同时存在下的偏振复用系统解复用有很大优势。因此，本文采用基于负熵最大化的不动点复数ICA算法对PMD和PDL同时存在时的偏振复用系统进行解复用，得到了很好的解复用效果，证明了ICA算法可以成功消除PMD和PDL并存时造成的串扰。

2 ICA算法与偏振解复用

2.1 ICA算法的基本思想

为了对ICA做出定义，首先需要设s为未知的源信号，x为观测到的混合信号，A表示未知的混合矩阵，则

式(1)中的统计模型就是一个ICA模型，ICA算法的目标就是根据混合信号 x，估计出可能的源信号s和混合矩阵A[14]。

为了达到目标，ICA算法中要做的核心工作就是找到一个分离矩阵W，并使它满足条件

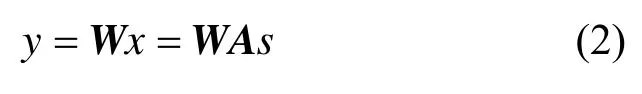
其中，y代表ICA估计出的源信号。当y中的分量相互之间统计独立时，则可以看作是源信号s的近似估计。

2.2 基于负熵最大化的不动点复数ICA算法

自1988年被提出以来[15]，ICA算法不断发展，出现了很多分支。对于一个偏振复用系统，通常采用 QPSK或 QAM 等高阶调制格式（本文采用QPSK），每路信号分别有I、Q 2个支路，需要对两路复数信号进行分离，所以应选择用复数ICA算法进行解复用。2008年，NOVEY M与ADALI T提出基于负熵最大化的不动点复数ICA算法(T-CMN算法)[16]。T-CMN算法的主要优势在于能将代价函数和源信号分布相匹配，尤其对于非圆信号来说这种算法的顽健性很强。考虑 T-CMN算法对不同调制格式的信号都有较好的适应性，本文将其引入偏振复用系统的解复用，以实现对偏振系统输出信号的有效分离。

T-CMN算法对独立成分的估计过程主要分为6个步骤。

1) 对观测数据x进行白化处理，得到z = V x。

2) 初始化矩阵 wi,i = 1 ,… ,n ，使其具有单位范数。

3) 更 新 wi, wi←- E ｛G*（y） g （ y） x ｝+E｛g （ y） g*（y ） ｝wi+E ｛ xxT｝E ｛ G*（y） g'（ y ）｝wi*。

4) 利用 W ← (W WH)-1/2W正则化 W = [w1,…,wn]T。

5) 若W未收敛则返回步骤3)。

6) 利用 y =WHx估计出源信号。

3 仿真系统与结果

本文仿真所用的偏振复用系统结构如图1所示。在VPI系统中进行仿真时，偏振复用系统的发送端使用了2个集成的QPSK信号发送模块，设置激光器的输出光分别为x和y方向的线偏振光，发送的光信号波长为1 550 nm，线宽1 MHz，比特率为 56 Gbit/s，经偏振合束器（PBC）复用后送入单模光纤进行传输，复用后系统传输速率为112 Gbit/s。为了更接近实际的通信系统，采用两段含有PMD的单模光纤与一个集总的PDL元件的级联模型[17]。两段光纤长度均为20 km，偏振模色散系数设置为 0.05ps/km，PDL设置为1 dB。

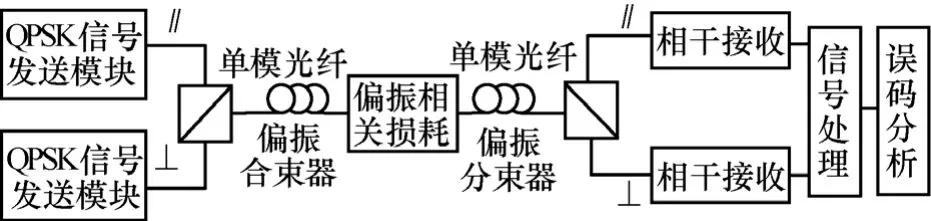
图1 偏振复用系统结构

在接收部分，考虑到本系统为偏振复用系统，因而相干接收部分采用了通用的偏振分集相干接收机，这样既能测量输入信号的复振幅，同时还可以控制输入信号的偏振态。偏振分集相干接收的结构如图2所示[18]，由2个偏振分束器（PBS）将输入信号光和本振光（LO）分为x、y 2个方向的正交偏振光，这4路偏振光按偏振态分为两组，分别输入2个独立的90°混频器进行混频，之后经过平衡检测器（BPD）检测，得到4个有串扰的信号分量IPD1～IPD4，由此得到两路相互串扰的偏振复用信号 Ix、 Iy，分别为

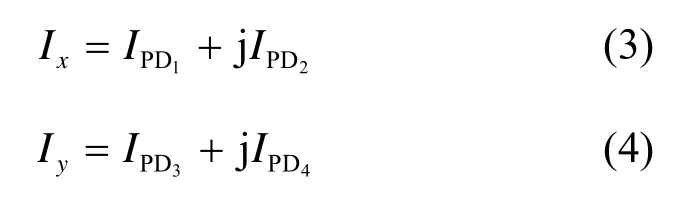
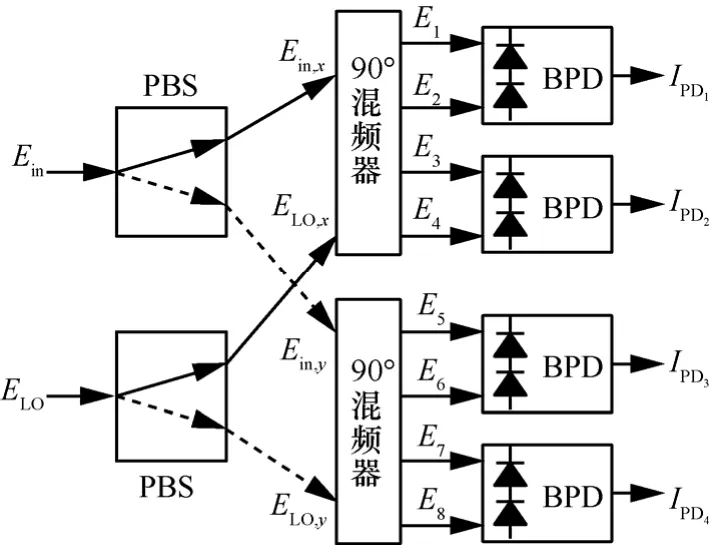
图2 偏振分集相干接收结构

随后两路相互串扰的偏振复用信号xI、yI进入DSP部分，DSP部分主要完成解复用和相位恢复两部分功能。两路信号首先由ICA算法进行解复用，消除PMD和PDL导致的信号间串扰；然后由载波相位恢复程序对QPSK信号进行相位恢复。最后输出的结果经解调后输入误码分析部分，计算误码率。

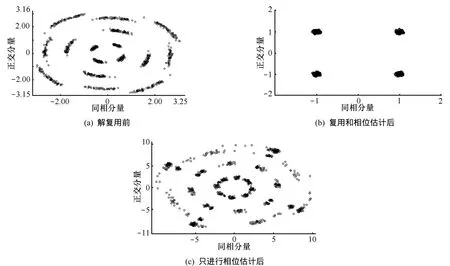
图3 信号星座图对比

图3(a)为未进行解复用前的原始信号星座图，可以看出信号点分布散乱，幅度和相位均有较大失真，传输质量极差。图3(b)是经ICA算法解复用和相位估计后的信号星座图，此时的QPSK信号很好地分布在星座图的4个相位点上，传输质量大幅度提高。作为对比，图3(c)给出了只进行相位估计（未经ICA处理）后得到的信号星座图，从星座图中信号点的分布情况可以看出此时信号依旧严重失真，这表明ICA解复用在消除信号串扰、改善传输质量方面起了决定性的作用。

图4中给出了解复用前和经过解复用及相位估计后的 I、Q两路信号眼图，可以看出解复用前信号眼图基本没有张开，码间串扰很大，信号存在严重畸变。经过解复用和相位估计之后，眼图张开大而清晰，信号传输质量明显改善。

4 噪声性能分析

为了重点分析偏振复用系统中PMD和PDL同时存在时ICA算法的解复用效果，以上的实验仿真过程中并没有考虑噪声因素。然而，在一个实际的通信系统中噪声是必然存在的。因此，下面将在偏振复用系统中加入噪声，得到系统中含噪声时的解复用效果。

系统误码率随OSNR的变化曲线如图5所示。结果表明：当系统中OSNR大于20.86 dB时，系统的误码率低于10-9，满足通信系统对误码性能的要求。图6和图7分别为OSNR等于20.86 dB时系统输出信号的星座图和眼图，可以看出信号的传输质量较好，可以保持正常通信。

图4 信号眼图对比

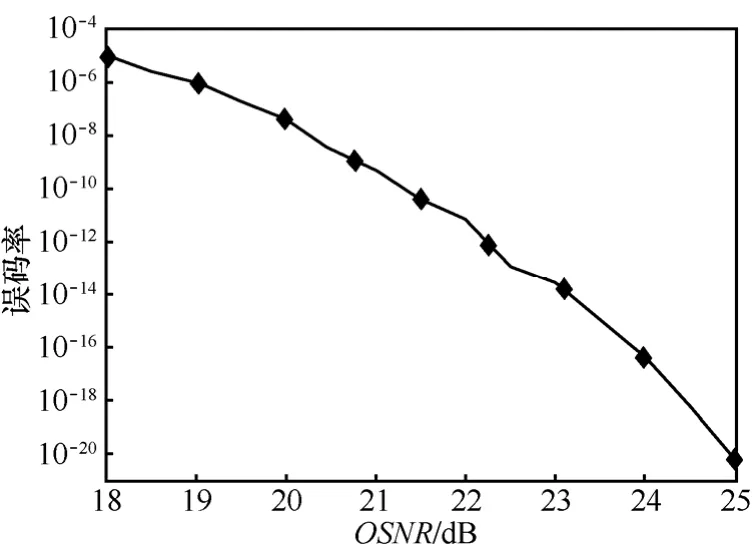
图5 系统误码率随OSNR的变化

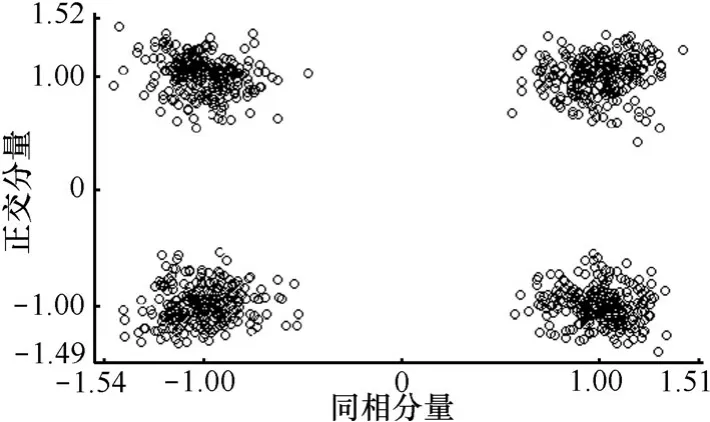
图6 噪声条件下信号星座（OSNR=20.86 dB）

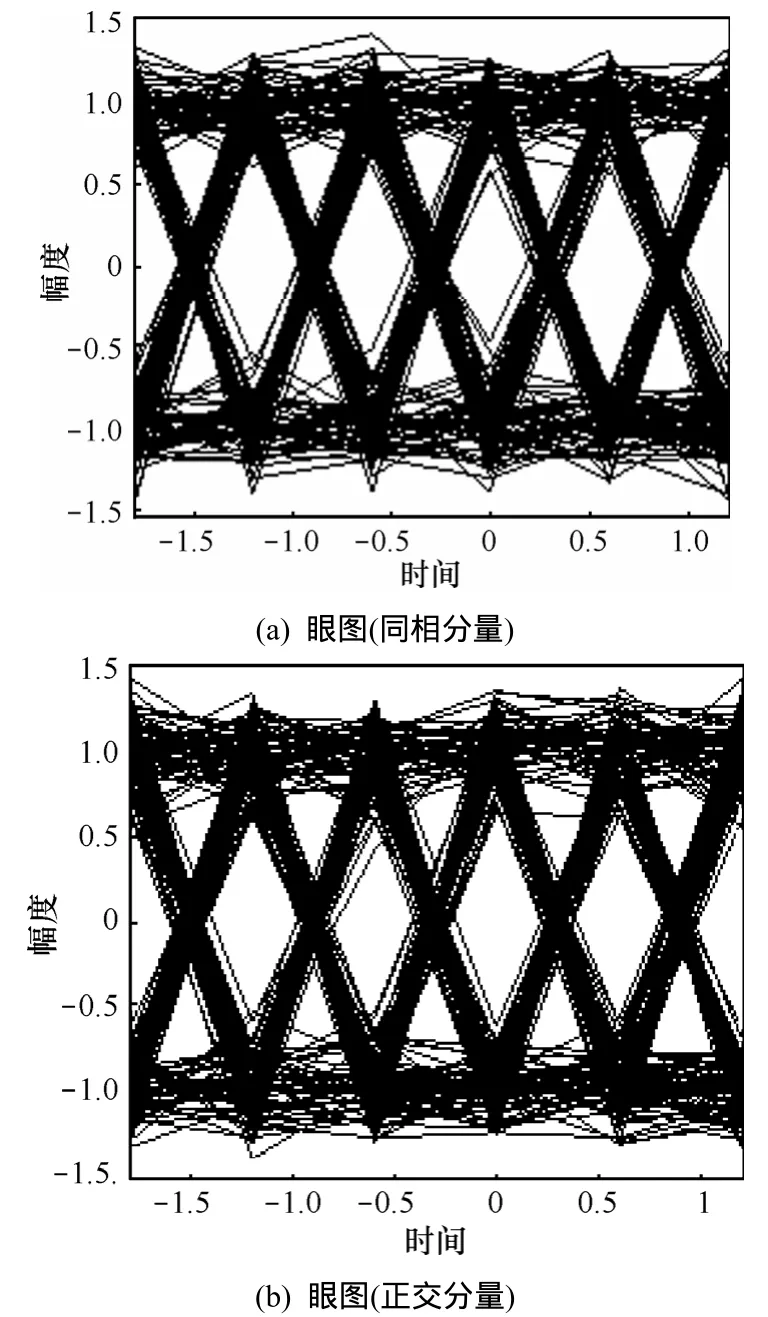
图7 噪声条件下信号眼（OSNR=20.86 dB）

5 结束语

本文采用基于负熵最大化的不动点复数 ICA算法（T-CMN算法）对同时存在PMD和PDL的偏振复用系统进行了解复用。通过观测星座图和眼图可以看出，经ICA算法解复用后，系统性能明显改善，噪声容限为20.86 dB。结果表明，T-CMN算法能够在PMD与PDL同时存在的情况下很好地实现偏振解复用。

[1] HECKER N E, GOTTWALD E, KOTTEN K. Automated polarization control demonstrated in a 1.28 Tbit/s (16×2×40 Gbit/s) polarization multiplexed DWDM field trial[A].European Conference on Optical Communication 2001[C]. Amsterdam, Netherlands, 2001. 86-87.

[2] CHO P S, HARSTON G , KERR C J. Investigation of 2-b/s/Hz 40-Gb/s DWDM transmission over 4×100 km SMF-28 fiber using RZ-DQPSK and polarization multiplexing[J]. IEEE Photonics Technology Letters, 2004, 16(2)：656-658.

[3] POOLE C D. Optical Fiber Telecommunications Ⅲ A[M]. New York：Academic, 1997.

[4] 王铁城.偏振模色散和偏振相关损耗效应在偏振复用中的影响[D].天津：天津大学，2008.WANG T C. PMD and PDL Effects in Polarization Division Multiplexing Transmission[D]. Tianjin： Tianjin University, 2008.

[5] WANG Z, XIE C, REN X. PMD and PDL impairments in polarization division multiplexing signals with direct detection[J]. Optics Express,2009, 17(10)：7993-8004.

[6] RENAUDIER J, CHARLET G, SALSI M. Linear fiber impairments mitigation of 40-Gbit/s polarization-multiplexed QPSK by digital processing in a coherent receiver[J]. Lightwave Technol, 2008, 26(1)：36-42.

[7] NELSON L E, WOODWARD S L, FOO S, et al. Performance of a 46-Gbps dual-polarization QPSK transceiver with real time coherent equalization over high PMD fiber[J]. Lightwave Technol, 2009, 27(3)：158-167.

[8] LAPERLE C, VILLENEUVE B, ZHANG Z. WDM performance and PMD tolerance of a coherent 40-Gbit/s dual-polarization QPSK transceiver[J]. Lightwave Technol, 2008, 26(l)：168-175.

[9] SUN H, WU K T, ROBERTS K. Real-time measurements of a 40 Gbit/s coherent system[J].Optics Express, 2008, 16(2)：873-879.

[10] SHTAIF M. Performance degradation in coherent polarization multiplexed systems as a result of polarization dependent loss[J]. Optics Express, 2008, 16(18)：13918-13932.

[11] XIE C. Polarization-dependent loss induced penalties in PDM-QPSK coherent optical communication systems[A]. OFC 2010[C]. San Diego,USA, 2010.

[12] VASSILIEVA O, HOSHIDA T, WANG X. Impact of polarization dependent loss and cross-phase modulation on polarization multiplexed DQPSK signals[A]. OFC 2008[C]. San Diego, USA, 2008.

[13] TOSHIHIKO H, TOSHIYUKI H, YUTARO T. PMD-induced crosstalk in ultrahigh-speed polarization-multiplexed optical transmission in the presence of PDL[J]. Journal of Lightwave Technology, 2011, 29(19)：2963-2970.

[14] HYVARINEN A, KARHUNEN J, OJA E. 独立成分分析[M]. 北京：电子工业出版社, 2007.HYVARINEN A, KARHUNEN J, OJA E. Independent Component Analysis[M]. Beijing： Publishing House of Electronics Industry, 2007.

[15] JUTTEN C, HERAULT J. A neuromimetic solution for the problem of sources discrimination[J]. Traitement Du Signal,1988,5(6)：389-403.

[16] NOVEY M, ADALI T. Complex ICA by negentropy maximization[J].IEEE Journal on Neural Networks, 2008, 19(4)：596-609.

[17] 戴峰, 杨伯君, 张晓光等. 偏振相关损耗和 PMD 共同作用对群时延带来的影响[J]. 现代有线传输, 2005,(3)：59-62.DAI F, YANG B J, ZHANG X G , et al. The influence of PDL and PMD on group time delay[J]. Modern Cable Transmission, 2005,(3)：59-62.

[18] TSUKAMOTO S, ISHIKAWA Y, KIKUCHI K. Optical homodyne receiver comprising phase and polarization diversities with digital signal processing[A]. ECOC 2006[C]. Paris, France, 2006.1-2.