武汉市流动人口影响因素的因子分析

朱祥和 (华中科技大学武昌分校基础科学部，湖北 武汉 430064)

沈 敏 (湖北省电力勘测设计院，湖北 武汉 430040)

武汉市流动人口影响因素的因子分析

朱祥和 (华中科技大学武昌分校基础科学部，湖北 武汉 430064)

沈 敏 (湖北省电力勘测设计院，湖北 武汉 430040)

通过因子分析找出影响武汉市流动人口的主要因素，预测了未来10年武汉市流动人口数量。

流动人口；因子分析；等维灰数递补动态预测

流动人口是国家和社会的财富，对城市的发展做出了巨大贡献。然而，流动人口的管理是各个城市都面临的棘手问题，因此，了解流动人口的数量和影响城市流动人口的主要因素具有极为重要的现实意义。目前，对于影响人口因素的分析方法有很多，如主成分分析法、逐步回归分析法、多层次分析法等。因子分析是主成分分析的推广与发展，它将具有错综复杂关系的变量综合为少数几个因子，以再现原始变量和因子之间的相互关系，同时根据不同因子对变量进行分类，属于多元分析中处理降维的一种实用方法[1]。

1 近10年武汉市流动人口数据

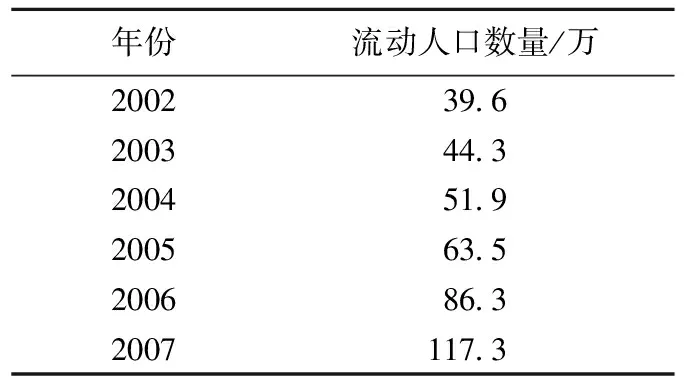
表1 近10年武汉市流动人口数据表

首先，通过统计年鉴仅能查找到武汉市1998～2002年以及2007年流动人口数据，对于数据的缺失，运用等维灰数递补动态预测法，估计出2003～2006年以及2008～2011年的流动人口数据。由于流动人口规模的迅速扩大主要是在1998年以后，这就使得能够掌握的流动人口数据的统计年限不长，如果利用灰色系统中常用的灰色动态模型 GM(1,1)直接预测未来流动人口的状况，会因为数据变化较大，模型所得预测灰区间过大，难以达到满意的结果。因此，采用修正了的“等维灰数递补动态预测”模型，其数学原理是：用已知数列建立的GM(1,1)模型预测得到第一个预测值(灰数)，将其补充在已知数列之后，同时去掉其第一个已知数据，保持数据序列的等维，然后再建立GM(1,1)模型预测下一个值，如此逐个预测，依次递补，直至完成预测目地或达到一定精度为止。其优点为:①及时补充和利用新的信息，提高灰色区间的白化度，即使预测灰数，在多数情况下也是有效信息；②每预测一步，灰参数作一次修正，模型得到改进，这样灰参数不断修正，模型逐步改进，因而预测值均产生于动态之中，结果如表1所示。

2 因子分析

在建立模型进行数据分析时，首先，考虑影响武汉市流动人口的主要因素，如反映经济发展状况的因子、反映居民生活的因子、反映公共服务的因子，反映市场物价的因子等。查阅武汉市统计年鉴，了解到近十年影响流动人口数量的10个指标的相关数据，分别是：GDP(x1)、社会消费品零售总额(x2)、第三产业生产总值比重(x3)、城镇居民人均年可支配收入(x4)、农村居民人均年纯收入(x5)、CPI(x6)、商品零售价格指数(x7)、城镇人口比重(x8)、城镇登记从业率(x9)、教育财政支出(x10)。通过SPSS软件进行因子分析，选择变量(流动人口)与影响因素之间进行数据处理[2-3]。

建立因子分析模型如下：

式中，X=(X1,X2,…,X10)′是原有的10个指标；F=(F1,F2,…,Fm)′称为X的公因子，即综合指标；aij为因子载荷，是第i个变量在第j个公共因子上的负荷；ε为X的特殊因子。

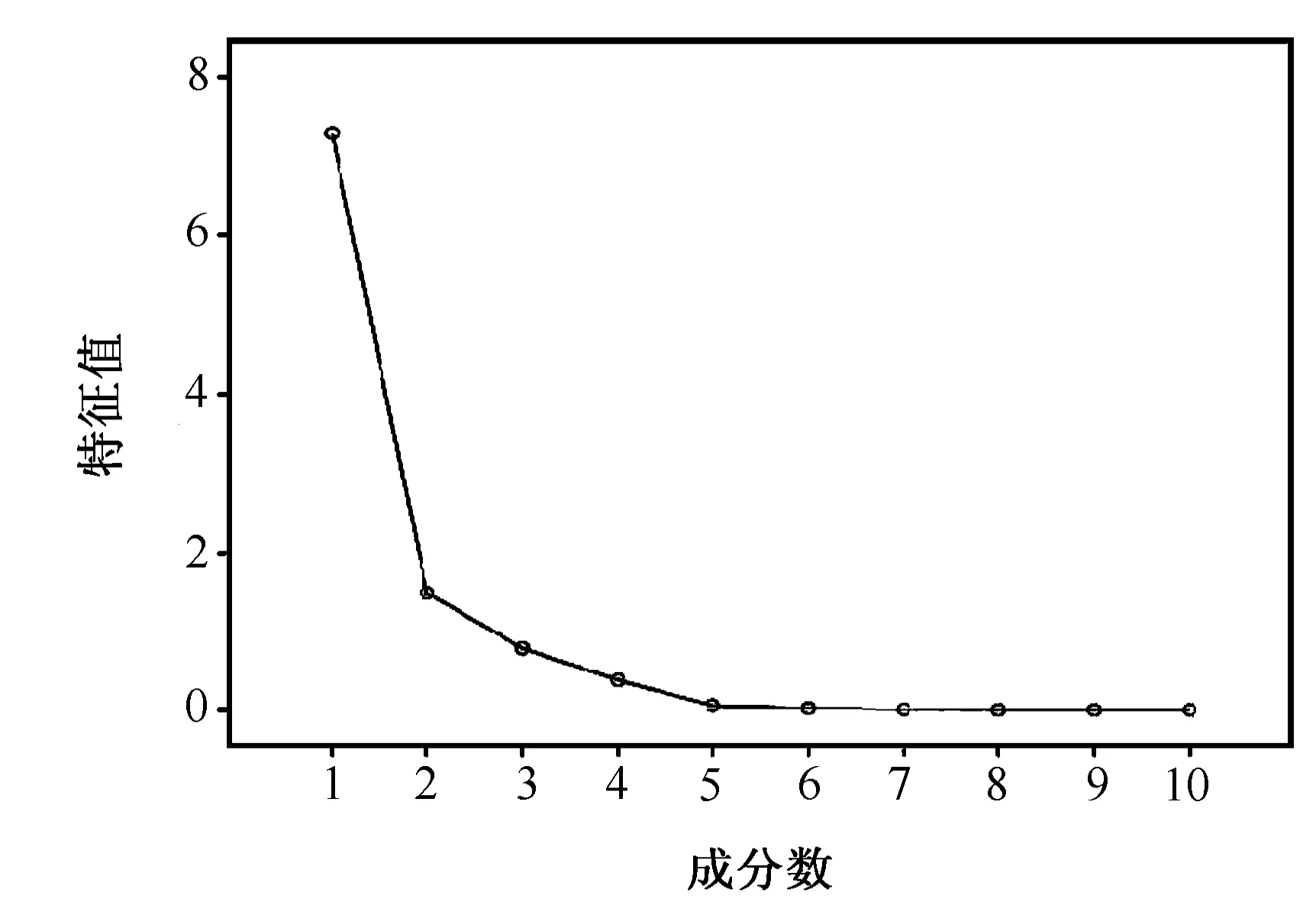
图1 特征碎石图

将数据调入SPSS软件，得到如下结果：

1)初始变量间相关性检验 由相关系数矩阵知，绝大多数的相关系数在0.5左右，而且对应的相关性检验Sig值大都小于0.01，说明变量间存在较为明显的相关性，适合因子分析。另外，在KMO检验和Bartlett球形检验中，KMO=0.638>0.5，Bartlett球形检验统计量Sig的值小于0.01，再次说明各变量间存在显著的相关性，能够进行因子分析。

2)公因子提取的方差 该数据中提取的变量共同度绝大多数都在85%以上，可见公因子对变量方差的解释效果很好。

3)方差解释表 首先对数据进行一致化和标准化处理，接着建立指标间的相关系数阵求出特征值和特征向量，画出特征值的碎石图，结果如图1和表2所示。

表2 方差解释表

表2显示，前2个因子的累积方差达到了87.624%，故而提取这2个公共因子就能够比较好的对问题进行分析。2个公共因子解释如下： 第1个公共因子(经济发展因素)代表教育财政支出、GDP、社会消费零售总额、农村居民人均年纯收入、城镇居民人均年可支配收入；第2个公共因子(价格因素)代表CPI和商品零售价格指数。从图1中，发现2个公共因子的特征变化趋缓，故而进一步说明选取2个公共因子是比较恰当的。

4)因子得分系数 由于公共因子能反应原始指标的相关关系，为便于描述研究对象的特征，需要用公共因子代表原始变量，即用指标的观测值来计算各个因子的得分，其数学模型为：

Fj=bj1X1+bj2X2+…+bj10X10j=1,2

式中,Xp为标准化后的数据。因子的得分系数如表3所示。

表3 因子的得分系数

5)综合评分 可对2个公共因子的得分(FAC1,FAC2)进行加权求和，权数就取其方差贡献率作为加权变量，得到综合得分ZF计算公式为：

ZF=56.630%×FAC1+30.994%×FAC2

由表4可知，前3年，第1因子得分高于第2因子，表明武汉市在当时价格因素方面比经济发展因素方面对流动人口的吸引力更大；而近2年，第2因子明显高于第1因子，说明影响武汉市流动人口的主要因素是经济发展因素。

表4 因子得分与综合得分

表5 未来10年武汉市流动人口预测表

3 流动人口预测

考虑阻滞增长模型[5]，采用曲线拟合的方法对未来10年人口进行预测，得到结果如表5所示。由表5可见，流动人口人数在逐年递增。如何加强管理，如何保障他们的社会权益，是急待解决的问题。从长远出发及时把流动人口的社会保障问题纳入建设规划，可为将来建立全民基本保障奠定基础[4]。

[1]杜强，贾丽艳.SPSS 统计分析从入门到精通[M].北京：人民邮电出版社，2009.

[2] 孙鹃娟，杜鹏，唐健.中国流动人口的养老保险状况及主要问题[J].北京行政学院学报,2011,5(1):13-16.

[3] 余甜甜,陈晔华.武汉市流动人口状况研究[J].统计与决策,2005,21(1):38-40.

[4] 黄健元,刘洋.流动人口预测模型构建及其应用[J].统计与决策,2008,23(1):42-46.

[5]冯守平.国人口增长预测模型[J].安徽科技学院学报，2008,6(1)：73-76.

2012-11-15

朱祥和(1981-)男，硕士，讲师，现主要从事概率统计方面的教学与研究工作。

O212.4

A

1673-1409(2013)04-0027-03

[编辑] 洪云飞