一种稳健的周期平稳信号的盲波束形成算法

高荣山

（中国电波传播研究所，山东 青岛 266107）

0 引言

传统波束形成算法（如MUSIC-SS多信号分离和ESPRIT信号子空间类算法）的实现需要导向向量、信号个数等先验信息，且性能受导向向量的估计误差影响非常大，期望信号向量与导向向量误差会严重恶化波束形成的性能，并且其分离信号个数受阵元数限制。而零点波束形成技术虽然可以抑制干扰信号，但受瑞利限的限制，其采用的干扰置零条件不一定是最佳的，可能降低干扰的同时增大输出噪声，从而使信干噪比得不到改善。盲处理算法的优点不需要先验信息，在通信领域应用越来越广，如分别针对信道编码的卷积码、分组码的盲识别算法[1-2]；在波束形成算法方面，由于通信中的绝大部分信号均存在循环平稳的性质，利用信号的循环平稳性能已经形成了很多应用和算法，如用于通信中信号检测器或频率估计[3-5]， W.A.Gardne等人提出的 SCORE(Self一 Coherence Restore)算法[6]，以及循环自适应波束形成算法CAB（Cyclic Adaptive Beamforming）算法[7]，这些算法利用信号的循环平稳特性进行波束合成，其优点是基于感兴趣信号(SOI，Signal of Interest)的循环频率的特性进行盲检测和识别，不需要其他的统计信息，如干扰信号个数、导向向量信息等。然而，实际中阵列输入中的干扰和噪声会使SOI的自相干性发生畸变，同时 SOI也会因多普勒频移等原因造成周期循环频率变化，从而造成周期频率的失配，周期频率误差由于存在sinc函数的零点效应，算法性能会随快拍数出现周期性的恶化；为提高算法的鲁棒性，一些学者提出了一些改进算法，如Y.T.Lee 等提出了基于传统 SCORE算法的两种改进算法[8]，然而这些改进算法是在提供附加的先验信息的基础上提出的；文中基于CAB算法，提出了利用信号干扰空间的权值来纠正导向向量的循环频率的失配的一种稳健的盲波束形成算法，仿真说明改算法对随机和非随机的周期频率失配条件下均能保持很好的性能。

1 周期平稳信号特性及信号模型

假设x(t)是一周期平稳信号，则必满足遍历性，从而可以用样本平均来估计其均值。

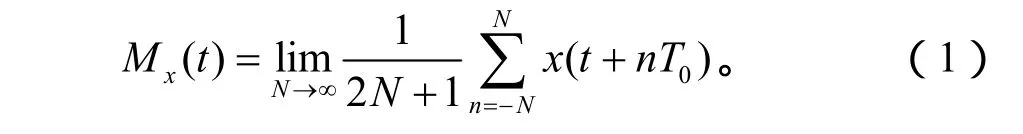
由于Mx(t)是周期为T0的周期函数，令m/T0=α，将其作Fourier级数展开，

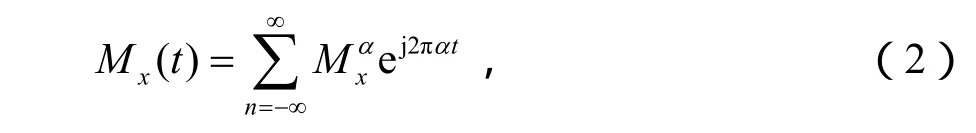
式中，Fourier系数

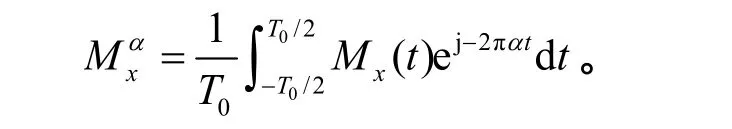
同样，x(t)的相关函数的周期也为T0，将其离散化，用Fourier级数展开，其Fourier系数可表示为

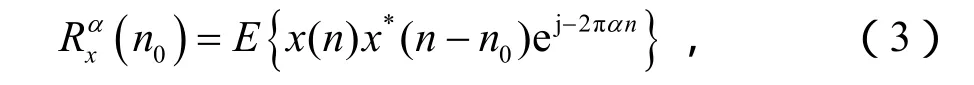
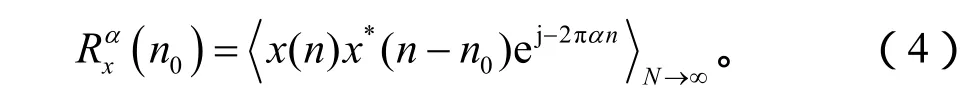
对于大多数人工信号，α往往取决于调制特性，如对AM信号，循环频率 α=2fc，fc为载波频率；对于BPSK信号，α=kfb,fb为调制波特率；对于高斯白噪声，在α≠0时循环相关函数均等于0。

考虑一个自适应波束形成器，天线由M个阵元组成，则接收信号为 M×1维向量，可以表示为期望信号，干扰和噪声的线性组合。即：

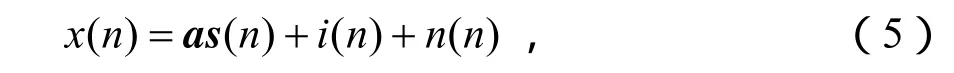
式中，a为窄带信号s(n)的导向向量，i(n)是窄带的干扰信号，n(n)为噪声；文中假设期望信号与干扰i(n)和噪声 n(n)均统计不相关，且期望信号与干扰信号的循环频率不相同。

2 CAB算法简介

波束形成算法为空间谱估计的一种应用，其的目的就是寻找最优权矢量 w，使得有用信号从阵列输出y(n)=wHx(n)中提取，去除不希望的信号的噪声。

为了利用信号的循环平稳特性，假定SOI即s(n)循环频率为α,定义阵列向量x(n)的循环相关矩阵：

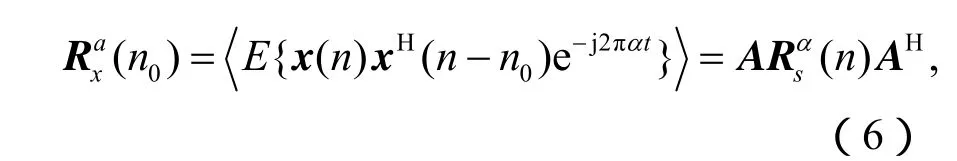
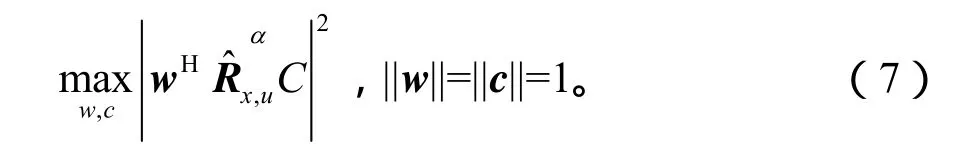
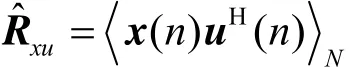
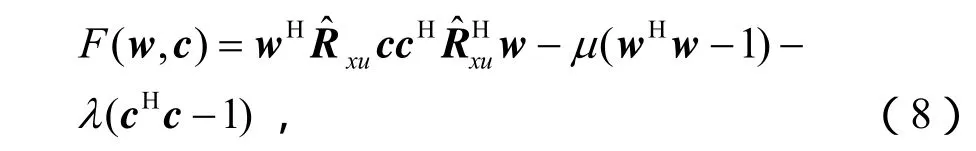
分别求关于w, c的偏导数，令其为零，可得到：

3 改进的CAB算法

文献[9]提出一种改进的 CAB算法，利用最小方差线性约束，提出了C-CAB算法，在w向量无失真相应的约束下，通过信号输出功率最小化求最优权值，所得结果为:

文献[10]提出了一种基于信号时空特征的波束形成算法，同时对信号进行空域和时域处理，提高算法的稳定性和性能，通过对阵列观测信号采样，求其相关矩阵，进行奇异值分解，所得的最大奇异值对应的奇异向量即为算法的最佳权向量，将其称为S-CAB算法，即基于空间的CAB算法。

将这两种算法的思想结合起来，提出基于子空间约束的SC-CAB算法，SC-CAB算法的中心思想是通过修正 CAB算法的信号干扰空间的权值来纠正导向向量的循环频率的失配。可通过下面的最优化问题解决：

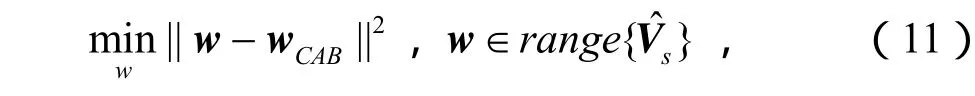
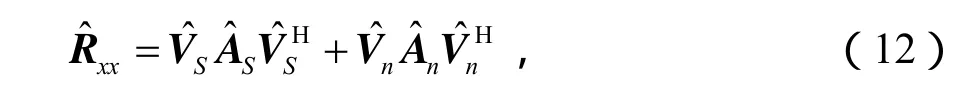
应用C-CAB算法的思想，可得SC-CAB算法的权向量可表示为：

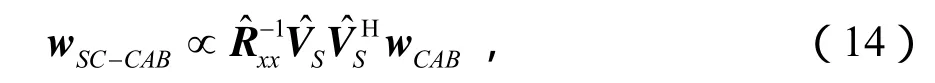
将式（12）代入式（14），得：

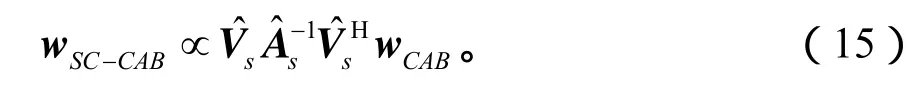
由于 S-CAB 算法中已经将wCAB、、求出，所以 SC-CAB算法只需增加计算式（15）的步骤即可。

4 计算机仿真

计算机模拟中，通过输出信号的信噪比来比较算法的性能。输出信号信噪比定义为：

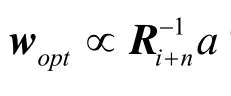
模型采用8元均匀线阵，d/λ=0.5, 信号形式为BPSK，归一化载频为0.1,噪声为空间白噪声，信噪比SNR=5 dB，入射方向为4º，干扰信号也为BPSK信号，归一化载频为0.2，入射方向为40º，干噪比INR为10 dB，快拍采样率为1 Hz，仿真分析了具有循环频率误差的算法的输出信干燥比情况。实验结果中，图1显示的是CAB、SC-CAB算法的数号信噪比，图2是不同算法对循环频率的失配后的性能比较。两种方法的模拟仿真结果都是50次独立实验的平均结果。

图1给出了输出SINR与样本数据的关系，数据长度为1200个点。从图1中可清楚地看出，随着快拍数的增加，CAB算法输出信干噪比会有小的周期性下降，SC-CAB算法接近最优解，具有更快的收敛行为，与CAB相比有明显的优势。

图2给出了波束形成器输出的SINR与循环频率不匹配的情况，纵轴表示SINR(dB) ,横轴表示失配度Δ。从图2中可看出，SC-CAB算法具有更好的稳健性。

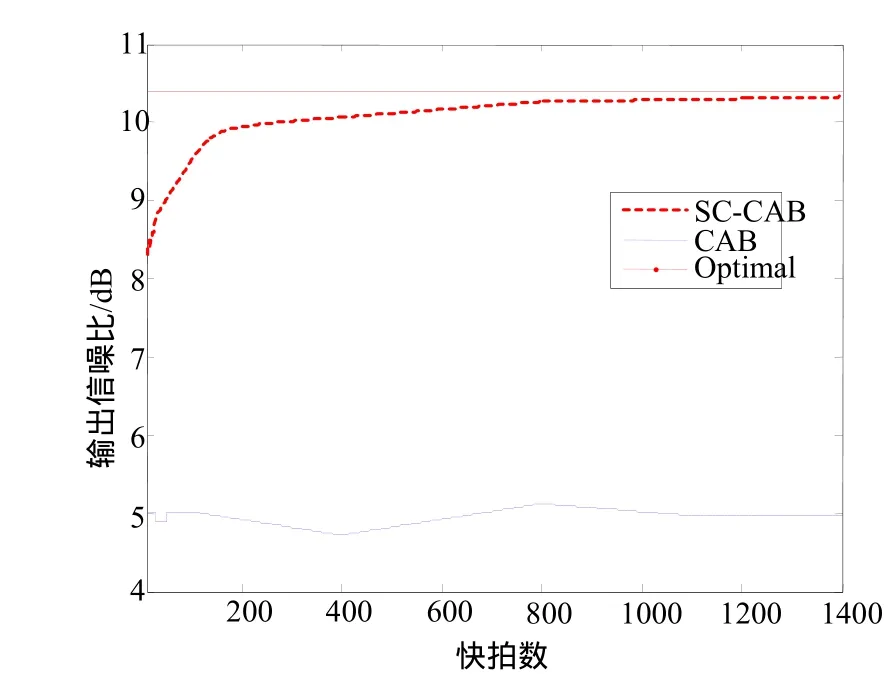
图1 CAB、SC-CAB算法的性能比较

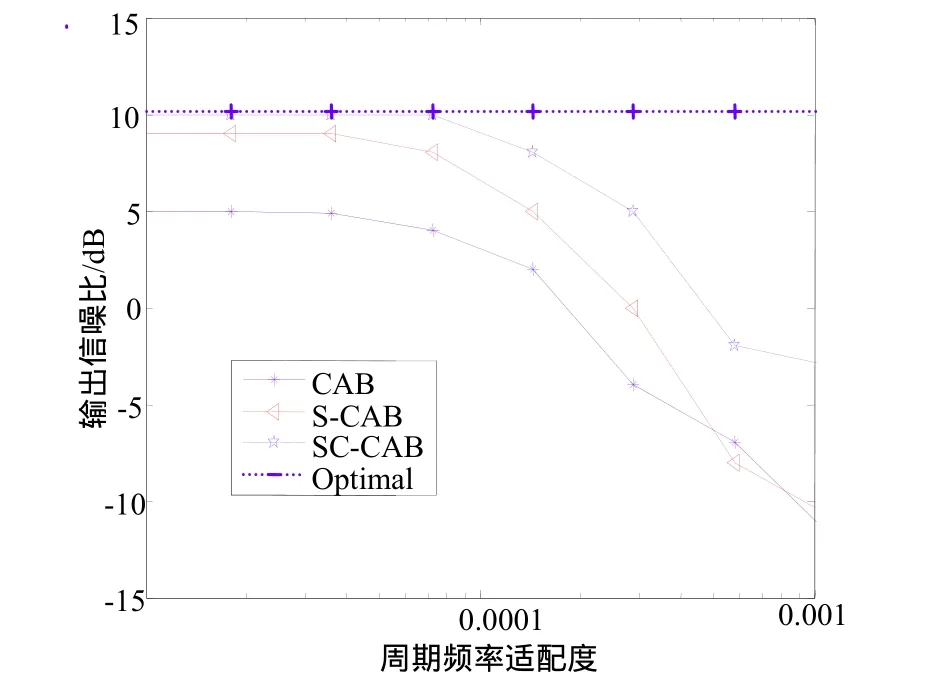
图2 算法的输出SINR与循环频率不匹配关系

5 结语

在传统CAB算法的基础上，针对循环频率的估计误差会降低算法性能，提出了一种稳健的基于信号周期平稳特性的自适应波束形成算法，对循环频率的失配具有较强的稳健性和适应能力。仿真实验结果表明了文中提出的方法既可以提高输出SINR，在估计循环频率有较大误差情况下仍有较好的性能。

[1]薛国庆,李易,柳卫平.系统卷积码盲识别[J].信息安全与通信保密,2009(02):57-60.

[2]底强,苏彦兵.二进制线性分组码盲识别问题研究[J].信息安全与通信保密,2012(08):74-77.

[3]张意忠,郭英.一种基于自适应方法的循环平稳信号检测器设计[J].通信技术,2009,42(09):44-46.

[4]崔小准,陈豪,胡光锐.OFDM系统频率和时间估计的循环平稳实现[J].通信技术,2003,36(03):45-46.

[5]尹万学,王可人.基于循环平稳特性的高速数传信号载频获取[J].通信技术,2008,41(05):35-37.

[6]AGEE B G,SCHELL S V,GARDNER W A.Spectral Self-coherence Restoral:a New Approach to Blind Adaptive Signal Extraction Using Antenna Arrays[J].IEEE,1990,78(04):753-767.

[7]GARDNER W A.Exploitation of Sepectral Redundancy in Cyclostationary Signals[J].IEEE ASSP Magazine,1991(04):14-36.

[8]LEE Y T,LEE J H.Robust Adaptive Arry Beamforming Wigh Random Error in Cycle Frequency[J].IEEE proc.-Radar,Sonar Navig.,2001,148(08):193-199.

[9]WU Q,WONG K M.Blind Adaptive Beamforming for Cyclostatioanary Signals[J].IEEE Trans.Signal Processing, 1996,44(11):2757-2767.

[10]吕泽均,肖先赐,南建设,等.一种稳健的循环时空波束形成算法[J].电子与信息学报,2003(06):741-746.