分布式电源的选址和定容

徐延波，卢京祥，刘苏云，徐 晨，蒋 丹，周 竞

（1.日照供电公司，山东 日照 276826；2.河海大学能源与电气学院 电力系统及其自动化，江苏 南京 211100；3.南京大学金陵学院，江苏 南京 210044）

0 引 言

分布式发电（DG）是指将发电系统以小规模（发电功率在数千瓦至50MW的小型模块）分散式的方式布置在用户附近，可独立地输出电能的系统［1］。按电源的不同DG分为两类:一类是可再生能源DG；另一类是不可再生能源DG。目前DG的研究热点之一是可再生能源发电技术，其中水利发电已经步入成熟，而风力、太阳能、潮汐等还在研究之中。分布式电源（DG）常以接入配电网运行为主，会对配电网的电能质量、供电可靠性、线路损耗、继电保护等方面产生影响，在不考虑配电网络的拓扑结构和负荷分布的情况下，其影响程度主要与DG的安装位置和安装容量分布密切相关［2］。

1 分布式电源的规划数学模型

由于连接到配电网的模型［3］既可简化为PV节点也可简化为PQ节点，本文将其当作有恒定功率因数的PQ节点；且分布式电源靠近负荷中心，假设分布式电源的位置在负荷节点上且安装分布式电源的个数为2个。此外由于配电网通常是辐射状，只有一个电源，线路潮流单相流动，而系统的保护也是根据这一特性来设计。为了保证分布式电源接入后电网潮流方向不发生变化，限制安装的分布式电源的容量不超过所在节点的负荷大小。由此可以将分布式电源的规划问题看作以下的数学模型，目标函数为网损最小，等式约束为各个节点的功率平衡约束方程，不等式约束为DG容量的约束，公式如下所示:

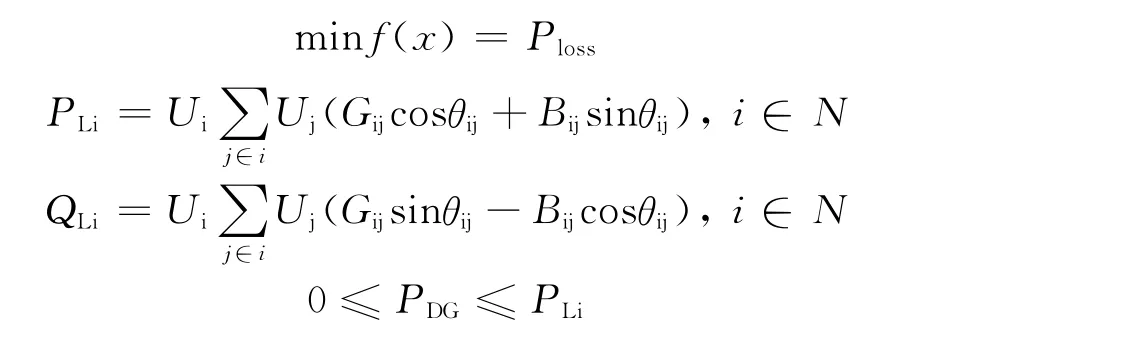
2 序优化理论

序优化理论［4－6］是一个能够有效解决单目标复杂优化问题的工具。并且序优化理论能够在复杂的目标函数和解空间的条件下，有较高的概率求得较好的解，能有效地提高计算效率，满足一般求解问题的需要。序优化理论的基本思路可表述为:

先从所有的解空间Θ中随机选取m个可行解，由这m个可行解构成新的可行解空间Θm，在所有可行解空间Θ中，取前n%个构成较好的解空间Θn，Θm中至少有一个解位于Θn中的概率为:

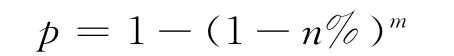
则构成新解空间的解个数m为:

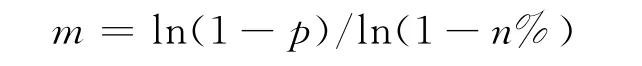
一般对目标函数进行序优化的步骤如下:

步骤一:从所有解空间按一定原则随机抽取m个可行解组成新的可行解空间。

步骤二:采用特定的选择规则对第一步中m个可行解来做快速的粗糙估计，排序后的可行解序号作为横坐标，其目标函数值作为纵坐标，近似的确定优化问题的类型。

步骤三:在确定OPC的类型后，取排序的前s个可行解作为选定的集合S，S的大小确定如下:

式中，z0、ρ、γ、η为曲线类型所对应的值；k、g 为预先给定的值，其中g的含义是新可行解集合Θm经过精确评估后的前g个足够好的解，k的含义是选定的集合S中要有至少k个真实的足够好的解。

步骤四:对S中所有的解进行精确的求解，再根据目标函数的大小对S集合进行排序，取目标值最好的解作为最终结果。

3 二次电流矩理论

上面步骤二和步骤四中都有对网损的计算，为了能够快速准确地计算网损，在步骤二中结合二次电流矩作为粗糙估计，从而可节省人力机时。一般辐射型配电网具有单相流动性的特点，对配电网中的节点与线路做以下两个规定:第一，支路的编号与支路流入的节点的编号相同；第二，规定相对的电流方向，在农村配电网中，对某一条线路，其流出节点为父节点，相对应的流入节点为子节点；而对于某一个节点，其流入支路为父支路，相对应的流出支路为子支路，为了更好地说明问题，对二次电流矩模型定义四个概念。

（1）回流路径Wi:若令根节点为n0，从网络中某个节点ni到根节点n0所经历的支路的集合就称为节点ni的回流路径。

（2）阻抗距离Zi:回流路径中所有支路的阻抗之和称为回流支路的阻抗距离:

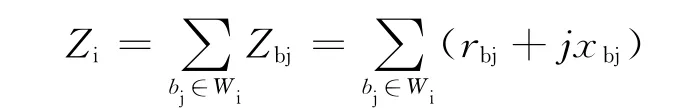
（3）等效二次电流:对网络中的某个节点，此节点的等效二次电流值为该节点的父支路中电流幅值的平方与该节点的子支路中电流幅值的平方之差。

（4）二次电流矩:定义回流路径的二次电流矩为T2Wi，公式为:T2Wi＝

并且由公式可知回流路径的Wi的电能功率损耗▽˙S（Wi）就是回流路径的二次电流矩T2Wi，即有:

经以上分析就可以给出用二次电流矩做粗糙评估的序优化方法的流程图，见图1所示。

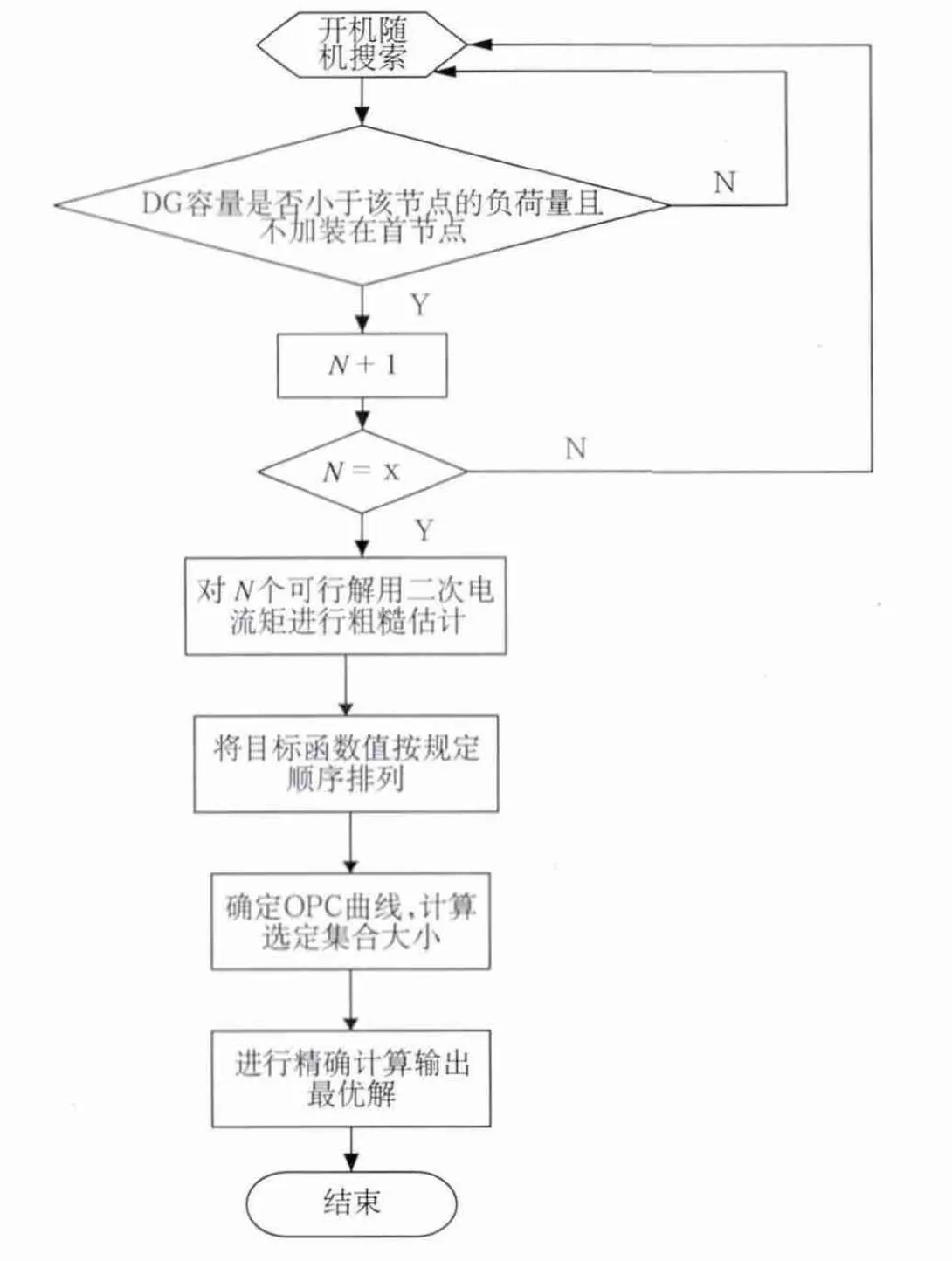
图1 结合二次电流矩的序优化方法选址定容流程图

4 算例

本文程序在 Matlab环境下编写，以10kV，33节点和某农村6kV，24节点配电网为算例，以网损最小为目标函数，基准功率为1MVA，如图2所示。

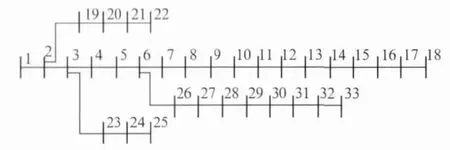
图2 33节点配电网网络拓扑图

这里装设两个分布式电源，其容量以0.05MVA为步长且不超过该节点的负荷容量，功率因数取λ＝0.9，可见此问题是一个离散量的优化问题。在上述条件的约束下，解空间不是很庞大，适当增加解空间容量，取新解空间为2600时，已经基本上能够反映整个解空间的情况。下面用二次电流矩对新可行解空间进行粗糙估计，计算结果按网络损耗来排序。

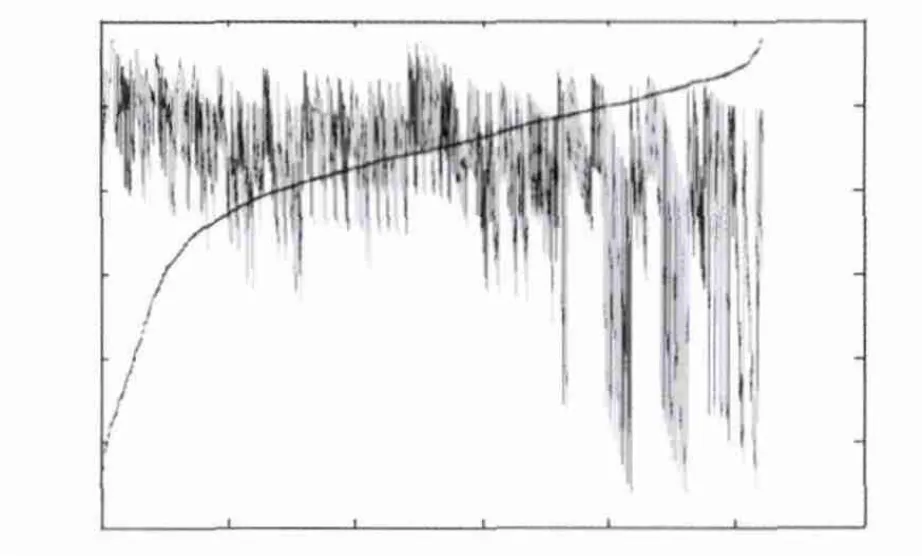
图3 33节点网损粗糙估计分析图

由图3可知，此曲线属于Bell型，令g＝20，k＝1，P＝95%。根据文献［8－10］中给定的参数值，Z0＝8.1998，ρ＝1.9164，γ＝ －2.025，η＝10，结合公式可以算出集合S的大小约为20个，现取前20个可行解进行精确计算，具体见表1所示。

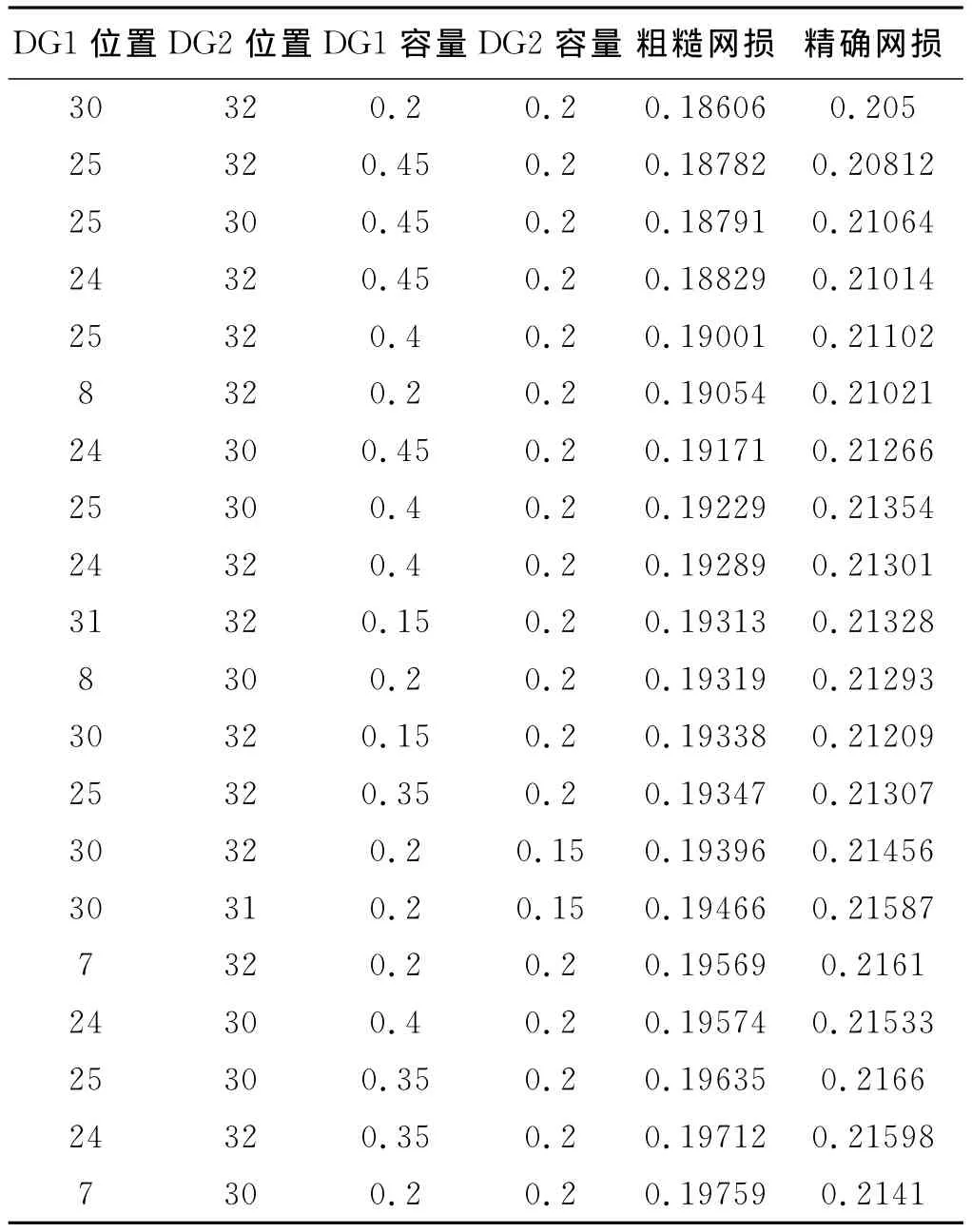
表1 前20个可行解的粗糙估计与精确计算

图4是粗糙估计和精确计算的趋势图比较。可见粗糙估计的值与精确值趋势一致，粗糙估计的排序合理。这里取最优解，即网损最小，精确网损为0.2110，而在加入分布式电源之前，通过潮流计算的网损是0.3180，说明了此方法对分布式电源的选址定容效果较好，起到了节能降损的作用。

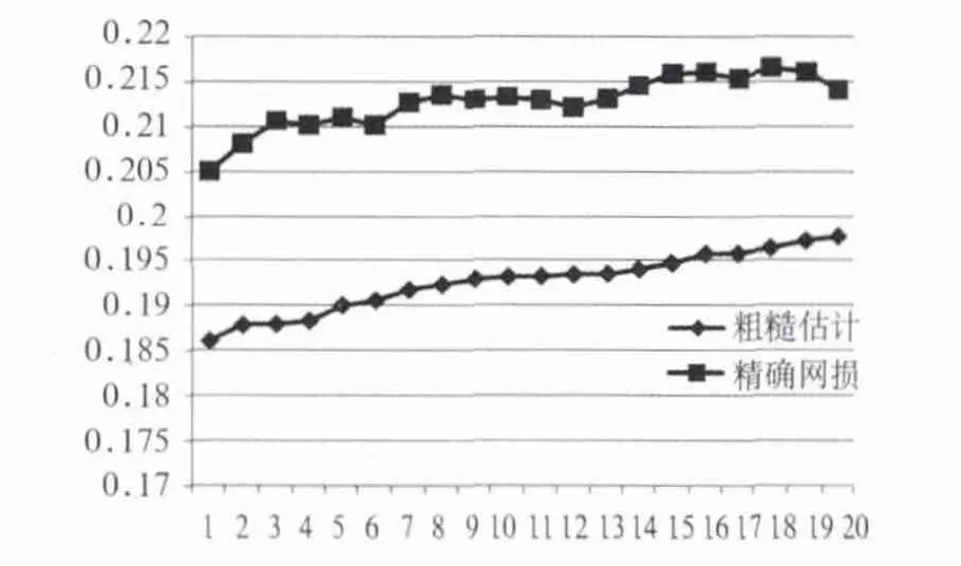
图4 粗糙估计与精确计算的损耗趋势图

对加入分布式电源的系统进行分析如图5。对加入前后的节点电压做对比，分析的结果是，加入DG前的平均电压为0.9220V，加入DG后的平均电压为0.9333V，电压水平有所改善，且电压水平普遍提高；此外，在接入分布式电源后，除去根节点之外的电压最高为0.99603V，没有出现电压超标的现象，电压提升最大的节点为末端的节点33，由原来的0.8736V提升到0.90422V，改善了末端电压偏低的现象；总体而言在降损的同时改善了原系统的电压质量，减轻了大电网的供电负担。

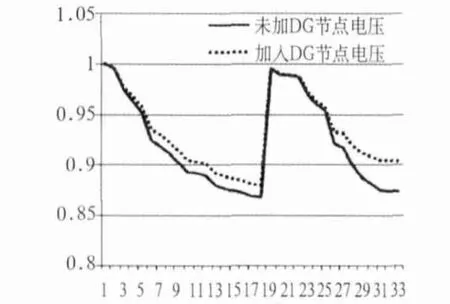
图5 加入DG前后负荷节点的电压变化图

5 结 论

本文将分布式电源的选址和定容的模型定位于网损和电压质量，充分运用二次电流矩理论可以快速计算线损的优点，将二次电流矩首先作为粗糙估计结合序优化理论知识充分发挥两种方法的优势，扬长避短，提高了效率，并通过对接入分布式电源以后网损和节点电压的分析证明此种方法的可行性，可对以后农村电网的分布式电源的选址和定容提供借鉴。

［1］唐小波，徐青山，唐国庆.基于“负荷质心”的分布式电源并网优化配置［J］.电力自动化设备，2011，31（2）:12－16.

［2］张俊潇.含分布式电源的20kV新型配电网规划［J］.陕西电力，2010，38（5）:57－60.

［3］熊一权.燃料电池发电技术［J］.中国电力，1998，31（9）:61－64.

［4］梁有伟，胡志坚，陈允平.分布式发电及其在电力系统中的应用研究综［J］.电网技术，2003，27（12）:71－75，88.

［5］Gubina A F，Gubina F，Golob R.Intelligent coordinative voltage and reactive power control［J］.Electrical Power and Energy Systems，2001，23（6）:313－321.

［6］Edward T W，Ho Y C.Universal Alignment Probabilities and Subset Selection for OrdinalOptimization［J］.Journal of Optimization Theory and Applications，1997，93（3）:455－489.

［7］白 茜.分布式发电对配电网电压调整作用的机理研究［D］.保定:华北电力大学硕士学位论文，2007.

［8］陈 琳.分布式发电接入电力系统若干问题的研究［D］.杭州:浙江大学博士学位论文，2007.

［9］王成山，陈 恺，谢莹华，郑海峰.配电网扩展规划中分布式电源的选址和定容［J］.电力系统自动化，2006，30（3）:38－43.

［10］张节潭，程浩忠，姚良忠，王 淳.分布式风电源选址定容规划研究［J］.中国电机工程学报，2009，29（16）:1－7.