“算两次”在自主招生解题中的应用

●

(嘉兴市第一中学 浙江嘉兴 314050)

“算两次”在自主招生解题中的应用

●沈晓飞吕峰波

(嘉兴市第一中学 浙江嘉兴 314050)

近几年自主招生的地位及权重逐渐提升，越来越受到师生的重视．由于自主招生实施的主体是高校，教育理念与高中有所不同，其命题风格及试题特点与高考也有一定的差异．作为优秀人才选拔模式的新探索，各高校的自主招生数学试题相对于高考数学试题而言，更加关注数学思维品质，强调数学学科和思想方法的考查．

笔者通过研究近几年的自主招生试题，发现“算两次”在自主招生解题中有着广泛应用．“算两次”又称富比尼原理，是指对同一对象从2种不同的角度去分析研究，从而找到解决问题的途径．在实际解题中，往往可以就线段的长度、数值的大小、模型的种数、函数的最值、事件的概率等“算两次”．

1 算线段的长度

例1如图1，用2个钢珠测算一工件的圆柱体内直径d，若半径为r1的钢珠上端与孔口平面距离为h1，半径为r2的钢珠上端与孔口平面距离为h2，则内直径d=______．

(2010年上海交通大学自主招生试题)

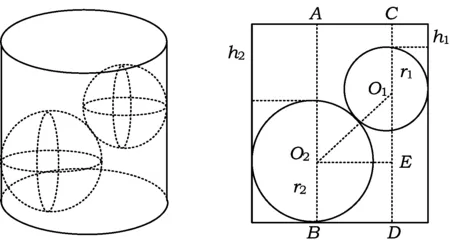
图1 图2

分析如图2，设O1E=x.因为AB=CD，所以

2r2+h2=r2+x+r1+h1，

即

x=r2-r1+h2-h1，

于是

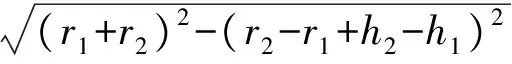
故内直径

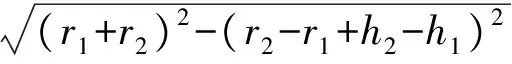
评注美国数学教育家波利亚说：为了得到一个方程，我们必须把同一个量以2种不同的方法表示出来，即将一个量“算两次”，从而建立相等关系.本题抓住圆柱体的高，利用AB=CD“算两次”，求出关键量O1E，从而使问题得到解决．

图3

例2在圆内接四边形ABCD中，AB=1，BC=2，CD=3，DA=4，求四边形ABCD的外接圆半径．

(2009年北京大学自主招生试题)

分析如图3，联结BD，设∠BAD=θ，则∠BCD=π-θ，设四边形ABCD的外接圆半径为R．在△ABD中，由余弦定理知

BD2=AB2+AD2-2AB·ADcosθ=17-8cosθ;

(1)

在△BCD中，由余弦定理知

BD2=BC2+CD2-2BC·CDcos(π-θ)=13+12cosθ.

(2)

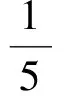
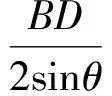
评注在△ABD和△BCD中分别计算BD，得到关于cosθ的方程，进而求出R．在实际解题中也可以就角的计算“算两次”．

2 算数值的大小

例3有个2 013×2 013的正方形数表，每行都成等差数列，每列各数平方后成等差数列．求证：左上角实数×右下角实数=左下角实数×右上角实数．

(2013年北京大学保送生试题)

证明记数表(如表1所示)左上角、右上角、左下角、右下角4个数分别为a,b,c,d，设最中间那个数为x．

表1 2 013×2 013的正方形数表

两边平方并化简，得ad=bc．若两者都取负号或者一正一负，同理可得ad=bc．

评注本题利用“中心开花”的思想，抓住表格中心的数值，分别从行和列2个不同的角度“算两次”，得到了所要求证的关系式．

3 算模型的种数

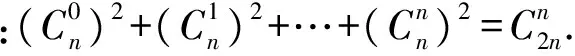
(2006年复旦大学自主招生试题)

(1+x)2n=(1+x)n(1+x)n=

展开后xn的系数是

解法2“鱼目混珠”问题.

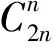
例5对正六边形的边和所有对角线染色，任意三角形3条边染色不同，任意2组三角形染色方式不同，求至少要染多少种颜色？

(2010年清华大学等五校联考试题)

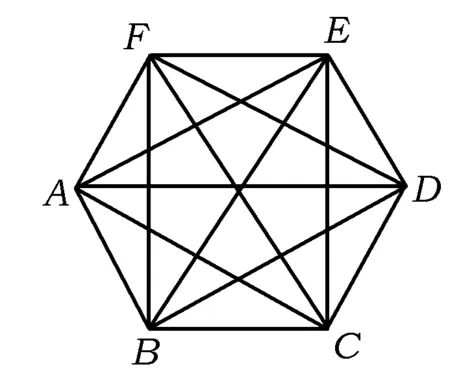
图4

另一方面，当n=7时，构造这样一种染色方案．记7种颜色为0，1，2，…，6．记六边形ABCDEF的6个端点对应数字1，2，…，6，按照这样的规则染色：每一条边染的颜色编号和该边2个端点对应数字之和相同(在模7下运算)，如：EF的2个端点编号之和为11，模7后为4，则染颜色4，以此类推.

在这样的染色方案下，若有2个三角形的染色方案完全相同，设2个三角形对应的顶点编号分别为a,b,c,a′,b′,c′.不妨设

a+b≡a′+b′(mod7)，

a+c≡a′+c′(mod7)，

b+c≡b′+c′(mod7),

则

2(a+b+c)≡2(a′+b′+c′)(mod7),

即

a+b+c≡a′+b′+c′(mod7),

从而a≡a′(mod7)，b≡b′(mod7)，c≡c′(mod7)，

故

a=a′，b=b′，c=c′.

即这2个三角形为同一个三角形，矛盾.因此,任何2个三角形的染色搭配都不一样.综上所述，最少染7种颜色即可．

评注本题即求证nmin=7．从2方面进行论证：(1)n≥6且n=6不满足条件，这说明nmin≥7；(2)构造了n=7时满足条件的例子，这说明nmin≤7．由(1)和(2)可知nmin=7．这种“算两次”的方法在求函数的最值时也经常用到．

4 算函数的最值

例6已知对任意x∈R，acosx+bcos2x≥-1恒成立，求(a+b)max．

(2009年北京大学自主招生试题)

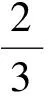
因此

a+b≤2．

恒成立．

综上所述，(a+b)max=2．

评注在本题中，若令t=cosx，则不等式转化为2bt2+at-b+1≥0，可以根据二次函数性质来分类讨论．这里用“算两次”的方法有效地回避了分类讨论，将其置于一般函数的知识背景下，在抓住本质的同时，使解答简洁、明快．

例7有100个容纳量相同的箱子，每个箱子内装2件货物，共200件．在取出来的过程中货物顺序打乱了，现要按一定的顺序将货物依次再装入箱子中，每个箱子最多装2件货物．若某货物能装入该箱子，则装入；若不能，则装入下一个箱子(如货物顺序为0.7，0.5，0.5，0.3，则第1个箱子到面前时放入0.7的货物，放不进0.5的货物，0.5放入下一个箱子，另一个0.5也放入该箱子，0.3放入第3个箱子，这样共需要3个箱子)．求最坏的情况下需要几个箱子．

(2010年清华大学自主招生试题)

分析一方面，这200件物品无论怎样摆放，一定可以将某2个相邻物品放入同一个箱子，否则记这200件物品质量为ai(1≤i≤200)，且箱子容纳量为M．不妨设随意摆放依次为a1,a2,…,a200，且

a1+a2>M,a3+a4>M,…,a199+a200>M，

相加得100M>100M，矛盾！

另一方面，构造一种情况说明198个箱子不能装下这200件物品．设

ai=100+(i-1)×0.01(1≤i≤200)，

且这200件物品依次摆放为a200,a3,a199,a4,a198,a5,a197,…,a103,a100,a102,a101,a2,a1,此时箱子容纳量M=201.99．可以验证，上述摆法只有重量为a101和a2的2个物品能放入同一个箱子，其余的每个物品都只能放在一个箱子中．

综上所述，至少需要199个箱子才能确保装下这200件物品，即最坏需要199个箱子．

评注需要的箱子数m相当于是这200件物品质量的多元函数，问题即求mmin．198个箱子不能放入说明mmin≥199，199个箱子能装入，说明mmin≤199．

5 算事件的概率

例812个人围坐在一个圆桌旁参加一个游戏，主持人给每人发一顶帽子，帽子的颜色包括红、黄、蓝、紫4种颜色．每个人都可以看见所有其他11个人帽子的颜色，但是不知道自己帽子的颜色．现在主持人让这12个人顺次来猜自己头上帽子的颜色．这12个人可以事先约定好一种策略，但是当游戏开始后不能进行交流，他们的目标是使12个人同时回答正确的机会最大．假定主持人给每个人发帽子的颜色是完全随机的，试给出一种策略，并分析在此策略下所有人都猜对的概率．

(2010年清华大学自主招生试题)

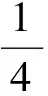
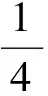
“算两次”从操作层面上来说要根据问题所给的题设条件选择一个适当的量，将其置于2种不同的知识、方法背景下分别考虑，然后通过所选取的适当量架起彼此间联系的桥梁来解决问题，其中可能涉及到“构造”的成分，除本文所涉及到的几个角度外，读者还可以从点、元素、交点、对子、子集等方面作进一步研究和探索．“算两次”从解题形式来说一般是这样的：一方面……;另一方面……;综合起来可以得到……．通过“算两次”来解决问题能有效地培养学生思维的发散性、形成创新意识、使学生体会到数学知识的内在联系及统一性．