一种低渗气藏单井产量递减计算方法及分析——以大牛地盒三气藏为例

罗 佼，闫长辉，2，何冠华，尹立明

（1.成都理工大学能源学院，四川成都 610059；2.“油气藏地质及开发工程”国家重点实验室·成都理工大学；3.中国石化西北分公司）

1 引言

几乎所有的油气田开发都要经历上产期、稳产期、和递减期［1］。对于实际的生产气井，一般可以通过压恢测试确定地层参数和地质储量［2］。由于低孔低渗气藏关井测试压力恢复较慢会给生产带来很大的损失［3］，所以有必要研究另一种不关井就能确定地层参数和地质储量的方法。为了避免关井给生产带来的损失，有必要研究根据气井（气藏）的生产史（气井的产量递减）反求地层参数和地质储量的方法。该方法的优越性在于，对于没有进行测试的气井可以根据现有的生产数据反求地层参数和地质储量［4］。20世纪80年代初，Fetkovich以均质地层不稳定渗流理论为基础，结合了Arps的经验公式，首次提出了现代产量递减曲线分析方法，该方法主要用于定压生产方式或可以假定为不变的生产数据［5］。Fetkovich产量递减模型不仅具有动态产量预测的功能，而且可以通过短期的产量测试资料的分析，直接计算地层流动系数、单井控制半径、表皮系数和控制储量等参数。Blasingame等人在前人研究的基础上提出了一种更为先进的现代典型曲线分析方法。该方法采用了归一化产量、物质平衡时间和拟时间概念，将变产量／变压降数据转变为等效定压力系统［6－7］，从而使产量递减规律分析方法的应用更为广泛。该模型具有动态产量预测、相关地层参数求取的功能，同时兼有预测精度高的特点，只是计算比较复杂。

本文基于国内外产量递减规律相关成果的研究，考虑大牛地气田盒三气藏的实际地质特征和开发动态特征，采用传统与现代相结合的产量递减分析方法进行递减规律分析。该方法是以Arps传统产量递减分析模型［8］为基础，利用Blasingame方法将其从定产量生产条件转化为定压生产条件，应用Fetkovich标准曲线图版进行拟合［9］，根据拟合匹配点进行储层参数计算和结合Arps方法得到气井产量递减规律［10］。

2 低渗气藏产量递减分析步骤

（1）根据Blasingame递减方法中（4）式计算物质平衡拟时间tcra，（5）式计算调整拟压力差Δpa（t），绘制如Δpa（t）／q（t）－tcra曲线图，通过曲线图拟合，得到（1）式中直线的斜率ma和ba，再结合（6）式，将定产条件下的拟时间转化为定压条件下的拟时间tcpa。

在定产量拟稳定流条件下新的气体流动方程为：

对于圆形封闭储层ba的表达式为：

物质平衡拟时间：

对调整压力（拟压力）的定义：

定量生产条件下拟时间与定压条件下拟时间的相互转换关系式：

上述式中：tcra——定产量下的物质平衡拟时间，d；Bg——气体体积系数，RB／Mscf（resm3／stbm3）；q（t）——t 时 刻 对 应 的 产 气 量，Mscf（std m3／d）；tcpa——定压力下的物质平衡拟时间，d；ρi、ρ——原始地层压力下的气体密度、压力为p下的气体密度，kg／m3；μi、μ——原始地层压力下的气体粘度、压力为p下的气体粘度，mPa·s；μt——平均压力下的气体粘度，mPa·s；Cti——初始条件下的综合压缩系数，Psia－1；Ct——平均压力下的综合压缩系数，Psia－1。

（2）绘制q（t）／Δpa（t）－tcpa双对数曲线图，并与Fetkovich图版进行拟合，再根据最接近的曲线选择不稳定期的re／rw＇值和衰竭期的b值。然后通过图版拟 合 得 匹 配 点 （q／Δpa）mp、（qDd）mp、（tcp，a）mp、（tDd）mp，将匹配点的值结合相关公式可算出气藏地层渗透率K、气体地质储量、泄气半径re等地层参数。

储层渗透率计算公式：

对于封闭圆形储层的渗透率：

单井控制储量G：

单井控制储层体积Vp：

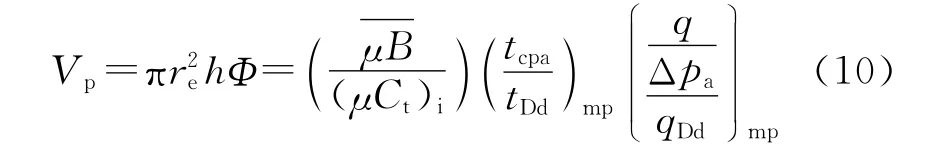
单井控制半径re：

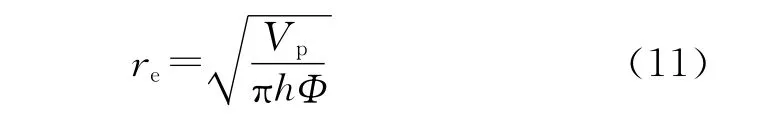
上述式中：Di——初始递减率，mon－1或a－1；G——原始地质储量，Mscf（stb m3）；Gp——累计产气量，Mscf（stb m3）；A——气藏含油面积，m2；h——地层厚度，m；K——地层渗透率，10－3μm2；Φ——孔隙度，%；qD——无因次产量；qDd——递减曲线无因次产量；rw——片筒半径，m；re——泄油半径，m；S——表皮系数；t——生产时间，d；tD——无因次时间；tDd——递减曲线无因次时间；Vp——储层孔隙体积，m3；Z——天然气压缩因子；Zi——原始地层压力下的天然气压缩因子。

（3）在（1）、（2）步的基础上，结合 Arps递减模型，计算递减期的初始产量qi和递减率Di，最后根据产量递减公式预测未来生产动态。

递减期的初始递减产量 ：

递减期的初始递减率：

未来产量的预测表达式：

其中：b为衰竭期的递减指数，常数。

（4）根据得到的产量预测表达式，计算递减阶段的产量，得到预测产量和实际产量的对比曲线图。若两者的变化趋势和数值大致相同，则表明得到的递减关系符合实际。

3 计算实例

本文在大牛地气田高产井、中产井、低产井中分别选取一口典型井进行分析，低产井以D1－112井为例，中产井以D1－4－52井为例，高产井D1－4－69为例。D1－112井、D1－4－52井、D1－4－69井构造位置均属鄂尔多斯盆地伊陕斜坡东北部。2005年10月20日至10月27日对D1－112井盒三气层进行了压裂试气作业，压后平均稳定气产量为1.4299×104m3／d，无凝析油及水产出，计算无阻流量为2.8228×104m3／d。按照本次研究分类标准，该井属于典型的低产井。2005年10月17日至10月25日对D1－4－52井盒三气层进行了压裂试气作业，压后平均稳定气产量为1.3045×104m3／d，凝析油产量0.06 m3／d，计算该层天然气无阻流量为6.7736×104m3／d。按照本次研究分类标准，该井属于典型的中产井。2006年10月20日到11月4日对D1－4－69井进行了压裂，平均稳定气产量为2.0612×104m3／d，无凝析油产出。计算该层天然气无阻流量为21.9932×104m3／d。按照本次研究分类标准，该井属于典型的高产井。

根据前文方法作出 Δpa（t）／q（t）－tcra图（见图1），通过直线拟合，得到各井ma，ba值如表1，其中ma是直线的斜率，ba是直线的截距。

图1 3口井 Δpa（t）／q（t）－tcra图

表1 拟合所得ma与ba值

根据公式（6）用所得ma与ba值将定量生产条件下拟时间转化为定压条件下拟时间。作q（t）／Δpa（t）－tcpa双对数曲线图，并与Fetkovich图版进行拟合，得到三口井的匹配点数值。根据匹配点的数值计算各井储层渗透率（公式8）和单井控制储量（公式9），如表2所示。可以看出计算值与岩心测试所得渗透率相比较为接近，说明应用该方法计算储层渗透率是可行的。同样，根据匹配点数值计算得到各井产量递减规律如表3所示。

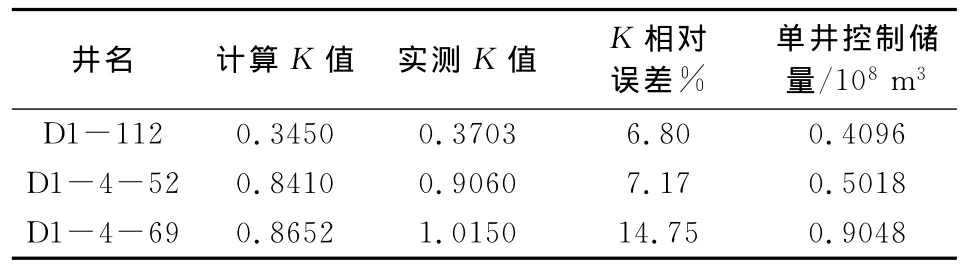
表2 计算渗透率和实测渗透率对比

作各井递减阶段实际产量、预测产量对比散点图如图2所示。可以看出各井产量预测结果和实际产量十分接近，表明本文所述方法得到的产量递减规律符合大牛地低渗气井的生产实际。

4 结论

（1）低孔低渗气藏压力恢复时间太长，以试井获得地层参数的方法成本过高，不适应于这类气藏。现代递减方法充分利用不稳定流阶段生产资料获得储层参数，计算结果具有一定的精度，真实可靠。

（2）根据拟合参数以传统Arps产量递减模型进行产量预测，预测结果表明所得产量递减规律符合气井实际生产。说明该方法进行产量递减分析是可靠的。

（3）由对低产井，中产井，高产井各一口的递减分析结果可以看出，该方法对于各个产量段的井都是适用的。

（4）该方法不仅具备了传统递减分析方法和现代产量递减分析方法的优势，还具备了求取地层参数简单、方便的特点。

表3 典型井产量递减规律

图2 各井递减阶段实际产量、预测产量对比散点图

［1］李传亮.油藏工程原理［M］.北京：石油工业出版社，2005：278－288.

［2］廖新维，沈平平.现代试井分析［M］.北京：石油工业出版社，2002：160－180.

［3］郝上京，王焰东，陈明强，等.低渗透气藏产量递减规律分析［J］.新疆石油地质，2009，30（5）：616－618.

［4］朱豫川，刘建仪，张广东，等.现代产量递减规律分析方法对比分析［J］.天然气勘探与开发，1998，17，（8）：28－31.

［5］Fetkovich M J.Decline curve analysis using type curves［J］.Journal of Petroleum Technology，1980，（6）：1065－1077.

［6］Blasingame T A，McCray T L，Lee W J.Decline curve analysis for variable pressure drop／variable flowrate system［C］.SPE21513，1991：23－24.

［7］Blasingame T A，Lee W J.The variable－rate reservoir limits testing of gas well［C］.Paper SPE17708 presented at the 1988 SPE Gas Technology Recovery Conference Midland，TX，March 13－14，1986.

［8］Aprs JJ.Analysis of decline cuvres［J］.Trans AME1945，160：228－247.

［9］Agarwal R G，Gardner D C，Kleinsteiber S W.Analyzing well production data using combined type curve and decline curve concept［C］.SPE57916，1998：27－30.

［10］史乃光.现代产量递减曲线分析方法及其应用［J］.天然气工业，1995，15（6）：53－57.