电光双稳混沌系统的广义同步和相位同步

高春歌，姜永恒，林晓珑

（吉林大学 物理学院，长春130012）

电光双稳系统在光通信、光开关和光存储等领域应用广泛.目前，该系统在锁频、混沌、混沌控制及信息存储方面的研究结果较多［1－5］，但对信号存储及通信保密领域混沌同步的研究结果较少［6－7］.混沌同步中广义同步和相位同步已在实验中实现，但由于同步发生时2个混沌系统的动力学变量存在较复杂的函数关系，因而不易被发觉［8－12］.广义混沌同步可通过计算系统全部李指数、找出2个系统间的函数关系及增加辅助系统3种方法判断是否同步，但相位同步不易确定.本文以电光双稳混沌系统为例，研究延迟反馈混沌系统间的广义同步和相位同步.通过分析最大条件李指数（MCLE），找出延迟反馈混沌系统实现广义同步和相位同步的规律，并研究对混沌系统的混沌控制和反控制.

1 混沌同步方案

在长延时条件下，电光双稳系统的动力方程可表示［1］为

其中：I为入射光的光强；xn（t）和xn＋1（t）为系统的状态变量；θ为初始相位；k为消光系数；n＝1，2，….在适当的条件下，该系统的状态可通过倍周期分岔过程进入混沌状态.

基于广义混沌同步的辅助系统判别法，本文提出一种实现混沌系统广义同步及完全混沌同步的新方法，如图1所示.该方法包含1个驱动系统和2个完全相同的响应系统.通过驱动系统和响应系统的差值信号驱动响应系统.于是电光双稳混沌系统的动力学方程可表示为：

图1 电光双稳系统混沌同步原理框图Fig.1 Scheme of chaos synchronization in electro－optic bistable systems

其中q为驱动强度.若q＝0，则3个系统相互独立；若q＞0，则驱动系统驱动2个响应系统.

2 数值仿真与分析

由混沌理论可知，当2个响应系统实现完全混沌同步时，驱动系统和响应系统即实现了广义混沌同步.由于MCLE描述了不同初始条件下系统相空间轨道的分离速度.因此，被驱动响应系统的MCLE＜0，表明当响应系统在相空间中的轨道分离呈指数衰减时，可实现2个响应系统间的完全混沌同步.即负的MCLE可作为是否实现广义同步的判据.

根据方程（2）～（4）可推得响应系统的MCLE表达式为

其中M表示计算时间.本文取M＞20 000.其他参数分别为k＝0.8，θ＝π，I1＝5.5，I2＝4.8，5.5，5.7.由文献［1］可知，驱动系统和响应系统取上述参数时均处于混沌状态.由式（5）可得响应系统MCLE随驱动强度的变化曲线，如图2所示.由图2可见，MCLE曲线存在2个负的MCLE区域，即为实现驱动系统与响应系统间广义混沌同步的参数区间.

图2 响应系统的MCLE随驱动强度的变化曲线Fig.2 MCLE of response system changes with the driving stiffness for different initial state

为说明2个区域内广义同步的差别，本文分析了驱动系统和响应系统的时序图，如图3～图6所示.其中图3和图4分别为驱动和响应系统处于不同混沌状态时2个系统间的同步情况.各参数分别为：k＝0.8，θ＝π，I1＝5.5，I2＝5.7.图3给出了系统在第一个负的MCLE区域时（驱动强度q＝0.2）响应系统和驱动系统状态间的关系.其中图3（A），（B）分别为驱动和响应系统的时序图及其差值信号的时序图.由图3（A）和（B）可见，驱动系统与相应系统间不存在关联，但由2个相应系统差值信号的时间序列（图3（C））可见，2个响应系统实现了完全同步.表明在第一个负的MCLE区域内，驱动系统和响应系统间可实现广义混沌同步.当系统处于第二个负的MCLE区域（q＝0.4）时，响应系统和驱动系统间的状态关系与图3相似.表明响应系统和驱动系统在第二个负的MCLE区域也可实现广义混沌同步.

图4和图5分别为驱动和响应系统处于相同混沌状态时2个系统间的关系，其参数分别为：k＝0.8，θ＝π，I1＝I2＝5.5.由图4和图5可见：当驱动系统和响应系统处于相同混沌状态时，在第一个系统负的MCLE区域内可实现响应系统和驱动系统间的广义同步，在第二个负的MCLE区域内可实现响应系统和驱动系统及2个响应系统间完全相同的混沌同步；当驱动系统处于周期态，响应系统处于混沌态时，随着驱动强度的增加，响应系统将由混沌态经分岔过程控制在不同的周期态，且控制达到的最小周期与驱动系统所处的周期相同，即实现了对混沌系统的稳定控制.控制方案仍可用式（2）～（4）表示，差别在于控制方案中的驱动系统或响应系统处于周期状态，而同步方案中二者均处于混沌状态.

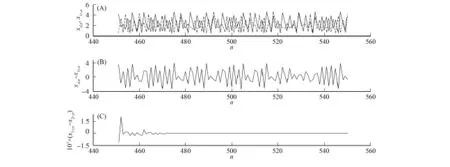
图3 初始混沌态不同时驱动和响应系统间的广义同步（q＝0.2）Fig.3 Diagram of generalized synchronization between drive and response systems initially in different chaotic states with q＝0.2

图4 初始混沌态相同时驱动和响应系统间的广义同步（q＝0.2）Fig.4 Diagram of generalized synchronization between drive and response systems initially in the same chaotic state with q＝0.2

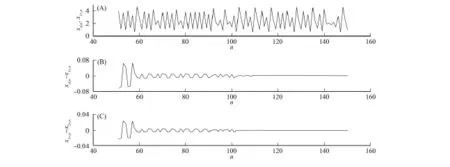
图5 初始混沌态相同时驱动和响应系统间的同步（q＝0.4）Fig.5 Diagram of identical synchronization between drive and response systems initially in the same chaotic state with q＝0.4

图6为响应系统在不同分岔强度下的倒分岔过程.参数分别为：k＝0.8，θ＝π，I1＝2，I2＝5.5，即驱动系统处于单周期态，响应系统处于混沌态.由图6可见，当响应系统处于周期态，驱动系统处于混沌态时，随着驱动强度的增加，响应系统进入混沌状态.这种现象称为对响应系统的混沌反控制.

图7为k＝0.8，θ＝π，I1＝5.5，I2＝4.8时响应系统反控制的分岔过程.由图7可见，驱动系统处于混沌态，响应系统处于4周期态.由于响应系统从4周期态直接进入4Ⅰ混沌区后进入1Ⅰ混沌区.因此，相同的方案通过改变初始条件，即可实现混沌同步、控制和反控制.

图6 响应系统在不同驱动强度下的倒分岔过程Fig.6 Inverse bifurcational diagram of response system with the driving stiffness increasing q

图7 响应系统反控制的分岔过程Fig.7 Bifurcation diagram of anti－control to the response system

综上，本文运用混沌理论提出一种实现延迟反馈系统间的混沌同步判别方法，并在此基础上研究了电光双稳系统广义同步和完全同步的规律.结果表明，通过改变系统初始条件，可实现电光双稳系统的混沌控制和反控制.

［1］GAO Jin－yue，Narducci L M，Schulman L S，et al.Hight－Order Bifurcation in a Bistable System with Delay［J］.Phys Rev A，1984，30（2）：901－905.

［2］ZHENG Zhi－ren，GAO Jin－yue.Dynamic Behavior of the Frequency－Locking in a Hybrid Bistable System with Delay and Input Modulation［J］.IEEE J Quantum Electronics，1996，32（3）：549－552.

［3］ZHANG Ying，LI Jian－bin，ZHENG Zhi－ren，et al.Dynamic Storage Function by Chaos Control in a Hybrid Bistable System ［J］.Phys Rev E，1998，57（2）：1611－1614.

［4］ZHENG Zhi－ren，GAO Jin－yue，DONG Po.Capacity of Dynamic Storage in an Electrooptical Bistable System［J］.IEEE J Quantum Electronics，2000，36（4）：425－429.

［5］WANG Xing－yuan，WANG Ming－jun.Chaotic Control of Logistic Map ［J］.Mod Phys Lett B，2008，22（20）：1941－1949.

［6］LI Dong，DENG Liang－ming，DU Yong－xia，et al.Synchronization for Fractional Order Hyperchaotic Chen System and Fractional Order Hyperchaotic Rössler System with Different Structure［J］.Acta Phys Sin，2012，61（5）：050502.（李东，邓良明，杜永霞，等.分数阶超混沌Chen系统和分数阶超混沌Rössler系统的异结构同步 ［J］.物理学报，2012，61（5）：050502.）

［7］Pecora L M，Carroll T L.Synchronization in Chaotic Systems［J］.Phys Rev Lett，1990，64（8）：821－824.

［8］Goodridge C L，Pecora L M，Carroll T L，et al.Detecting Functional Relationships between Simultaneous Time Series［J］.Phys Rev E，2001，64（2）：026221.

［9］Afraimovich V，Cordonet A，Rulkov N F.Generalized Synchronization of Chaos in Noninvertible Maps［J］.Phys Rev E，2002，66（1）：016208.

［10］Osipov G V，Hu B，Zhou C，et al.Three Types of Transitions to Phase Synchronization in Coupled Chaotic Oscillators［J］.Phys Rev Lett，2003，91（2）：024101.

［11］Kurth J，Boccaletti S，Grebogi C，et al.Control and Synchronization in Chaotic Dynamical Systems［J］.Chaos，2003，13（1）：126－127.

［12］Ticos C M，Rosa E J，Pardo W B，et al.Experimental Real－Time Phase Synchronization of a Paced Chaotic Plasma Discharge［J］.Phys Rev Lett，2000，85（14）：2929－2932.