一种改进的最近邻聚类算法*

李 婧

(重庆师范大学 数学学院，重庆 400047)

一种改进的最近邻聚类算法*

李 婧

(重庆师范大学 数学学院，重庆 400047)

传统的最近邻聚类算法一般采用欧式距离的计算准则，当各个分量的分布不一样时，采用欧式距离有着明显的缺点； 针对以上问题，采用标准化欧式距离的计算准则，将熵值法引入到算法中，提出了基于熵值法和标准化欧式距离的改进的最近邻聚类算法； 熵值法用来修订算法的标准化欧式距离计算公式，以提高算法的聚类精确程度.

聚类；最近邻算法；标准化欧式距离；信息熵

聚类[1]分析研究有很长的历史，几十年来，其重要性及与其他研究方向的交叉特性得到人们的肯定. 聚类是数据挖掘、模式识别等研究方向的重要研究内容之一，在识别数据内在结构方面具有极其重要的作用. 聚类就是将数据对象分成类或簇的过程，使同簇的对象之间具有很高的相似度，而不同簇的对象高度相异. 聚类分析的典型应用包括物种的分类和分子生物学中的基因分类，商业中对消费客户的分类，城市规划中的地理数据分析等等.目前存在大量的聚类算法，由于划分标准不明确，所以很难对聚类算法提出一个明确的分类. 根据数据在聚类中的积聚规则以及应用这些规则的方法，聚类算法有多种分类方法，本文将聚类算法大体划分为划分方法、层次方法、基于密度的方法、基于网格的方法等[1].

最近邻聚类算法是聚类算法中最基本的算法之一， 熵是热力学中的基本概念，文献[2]利用信息熵对数据对象的属性进行赋权，并利用权值来修改距离计算公式. 文献[3]研究了熵权法在股票市场上的应用. 文献[4]是基于熵的概念对其权重给予确定的一种新方法，对融合网络服务质量效率保障研究. 最近邻聚类法是聚类算法中最基本的算法，它普遍采用欧氏距离的计算准则. 由于欧式距离存在明显的缺点. 简单的来说，主要有两个缺点：一是在实际问题中对象包含许多种不同量纲的属性；二是没有考虑各个分量的分布(期望、方差等)可能不同. 鉴于此，本文提出了一种基于熵值法确定数据属性的权值，采用赋权的标准化欧式距离作为相似度测量依据的最近邻聚类算法，该算法较于传统的欧式距离算法在一定程度上提高了聚类的精确度和稳定性.

1 熵值法确定权值

1.1 相关定义

设待聚类的数据对象集为A={x1，x2，…，xn}，且向量xi=(xi1，xi2，…，xim)，xik是xi的第k(k=1，2，…，g)维属性，m为对象属性的维数，有如下定义：

定义1[7](欧式距离)设两个向量xi=(xi1，xi2，…，xim)和xj=(xj1，xj2，…，xjm)分别表示两个数据对象，则数据对象xi和xj之间的欧式距离：

定义2(标准化欧式距离) 数据对象xi和xj之间的标准化欧式距离计算公式：

其中sk为第k个分量的标准差.

1.2 熵值法改进距离计算公式

熵是热力学中的概念，最早由申农引入到信息论，主要用于测量系统的无序程度. 熵权法是一种可以用于多对象、多指标的综合评价方法.目前已经在工程技术、管理科学乃至社会经济等领域得到广泛应用[3].本文使用信息熵的概念度量属性权值的大小，得出赋权的标准化欧式距离计算公式.

使用熵值法确定权值的步骤如下：

1) 设有n个待聚类的数据对象，所有的数据对象包含m维属性，则属性值矩阵：

其中xij表示对象xi的第j维属性的度量.

2) 计算第j维属性对应的第i个数据对象的属性值比重：

其中rij为对象xi的第j维属性的属性值比重.

3) 计算第j维属性的熵值：

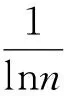
4) 第j维属性的权值[4，5]：

利用标准化的欧式距离及信息熵计算属性权值，将数据对象xi和xj之间的欧式距离计算公式修改为下式：

利用改进的距离计算公式可以更为精确的计算出各个数据之间的差距，在一定程度上提高了聚类精确程度.

2 基于熵值法的改进的最近邻聚类算法

2.1 最近邻聚类算法基本思想[6]

最近邻聚类算法是以全部训练样本作为代表点，计算测试样本与这些代表点的距离，即所有样本的距离，并以最近邻者的类别作为决策. 也就是说有n个待分类的模式样本{x1，x2，…，xn}，要求按阈值T分类到以z1，z2，…，为聚类中心的模式类中.

2.2 改进的最近邻聚类算法算法描述

输入：需要聚类的数据对象集A和阈值T；输出：以z1，z2，…，为聚类中心的聚类。任取一个模式样本xi作为第一个聚类中心的初始值，例如令x1=Z1；计算模式样本x2到x1的加权的标准化欧式距离D21=‖x2-x1‖若D21>T，定义一个新的聚类中心Z2=x2，否则x2∈以Z1为中心的聚类.假设已有聚类中心Z1，Z2，计算D31=‖x3-Z1‖和D32=‖x3-Z2‖若D31>T且D32>T，则建立第三个聚类中心Z3=x3，否则x3∈离Z1和Z2中最近者，即最近邻的聚类中心.依次类推，按照这种最近邻规则，直到将所有的n个模式样本全部分类.

3 结束语

本文结合熵值法和加权的标准化欧式距离提出了一种改进的最近邻聚类算法，熵值法用来计算对数据对象的各个属性的权值，用改进的权值修正加权的标准化欧式距离计算公式，以提高了聚类的精确度. 相比较与传统的最近邻聚类算法，改进的算法较之于传统的最近邻算法在算法的计算效率上有所提高，聚类的精确度明确增强.

[1] HAN J W，MICHELINE K. Data mining concepts andtechniques [M].Beijing： China Machine Press，2001

[2] 原福永，张晓彩，罗思标.基于信息熵的精确属性赋权K-means聚类算法[J].计算机应用，2011，31(6)：1675-1677

[3] 陈孝新.熵权法在股票市场的应用[J].商业研究，2004，(16)：139

[4] 陈雷，王延章.熵权法对融合网络服务质量效率保障研究[J].计算机工程与应用，2005，41(23)：1-3

[5] 高孝伟.熵权法在教学评优中的应用研究[J].中国地质教育，2008，17(4)：100-104

[6] 钟珞，潘昊等.模式识别[M].武汉：武汉大学出版社，2009，9

[7] 仝雪娇，孟凡荣，王志晓.对K-means初始聚类中心的优化[J].计算机工程与设计，2011(8)：2721-2723

Keywords：clustering；nearest neighbor algorithm；standardized Euclidean distance；information entropy

A Kind of Improved Nearest Neighbor Clustering Algorithm

LIJing

(School of Mathematics, Chongqing Normal University, Chongqing 400047, China)

The traditional nearest neighbor clustering algorithm commonly used Euclidean distance calculation rules, when the various components of the distribution are not the same, the using of Euclidean distance has obvious shortcomings.According to this problem, this paper uses standardized Euclidean distance calculation formula, by introducing entropy method to the algorithm, proposes the improved nearest neighbor clustering algorithm based on entropy method and standardized Euclidean distance. The entropy method is used to amend the standardized Euclidean distance calculation formula of the algorithm to improve clustering accuracy of the algorithm.

1672-058X(2013)10-0061-03

2013-03-13；

2013-04-20.

李婧(1988-)，女，重庆巫山人，硕士研究生，从事智能计算及应用研究.

TP273

A

责任编辑：代小红