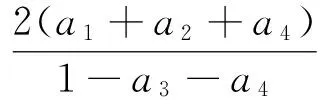广义非扩张映象的不动点定理

邓 红 彦

(重庆师范大学 数学学院，重庆 401331)

广义非扩张映象的不动点定理

邓 红 彦

(重庆师范大学 数学学院，重庆 401331)

引入一类更广泛于非扩张映象的一种映象，推广了Bogin和Gregus的结论，并对完备度量空间和完备凸度量空间上该映象的不动点定理给出了证明.

不动点；压缩；非扩张；凸度量空间

1922年，在Banach首次提出了压缩映象之后，人们相继提出非扩张映象、渐进非扩张映象、渐进拟非扩张型映象等概念，并取得了大量成果. 受文献[1-3]的启发，引入一种更广义的映象替代原来的映象，并得到相同的结论.

1 预备知识

设(X,d)是度量空间，满足：∀x,y∈X,有d(Tx,Ty)≤kd(x,y),k∈[0,1).则映射T：X→X,T为压缩映象,若k=1，则称T是非扩张映象.

定义1[1]T：C→C是Banach空间的子集C上的映射，称T满足“条件”(C)，如果

显然条件(C)弱于非扩张映象.

定理1[2]设(X,d)是非空完备度量空间，映射T：X→X，满足：

d(Tx,Ty)≤ad(x,y)+b[d(x,Tx)+d(y,Ty)]+c[d(x,Ty)+d(y,Tx)]

其中a≥0,b>0,c>0且a+2b+2c=1，则T有唯一一个不动点.

定义2[3]设(X,d)是度量空间，映射W：X×X×[0,1]→X，称W为X的凸结构，若满足：

d(u,W(x,y,λ))≤λd(u,x)+(1-λ)d(u,y);∀(x,y,λ)∈X×X×[0,1],∀u∈X

存在此类映射W的度量空间称为凸度量空间.

显然,在凸度量空间中可得到d(x,W(x,y,λ))≤(1-λ)d(x,y),d(y,W(x,y,λ))≤λd(x,y).

定理2[2]设C是Banach空间B中的非空闭凸完备度量空间，映射T：C→C，满足：

‖Tx-Ty‖≤a‖x-y‖+b(‖x-Tx‖+‖y-Ty‖),∀x,y∈C

其中a>0,b>0且a+2b=1，则T有唯一一个不动点.

2 主要结论

d(Tx,Ty)≤a1d(x,y)+a2d(x,Tx)+a3d(y,Ty)+a4d(x,Ty)+a5d(y,Tx)

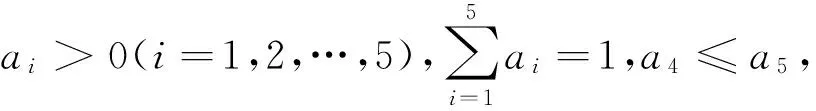
证明设dn=d(Tnx,Tn+1x)，其中d0=d(x,Tx).

所以

(1)

即{dn}是不增序列.

下证∀x∈X，∃k∈(0,2)，使得d(Tx,T3x)≤kd(x,Tx)成立.

第二种情况：d(x,T2x)

令a1+a2+a3+a4k=m，则有∀x∈X,d2≤md0(m<1).

矛盾.证毕.

下证∃y∈X，k<1，使得d(y,Ty)

下证T的不动点的唯一性.

d(u,v)=d(Tu,Tv)≤a1d(u,v)+a2d(u,Tu)+a3d(v,Tv)=a1d(u,v)

矛盾.证毕.

[1] POPESCU O.Two generalizations of some fixed point theorems[J].Computers and Mathematics with Applications, 2012(62)：3912-3919

[2] BOGIN J.A generalization of a fixed point theorem of Goebel[J].Kirk and Shimi Canad Math Bull,1976(19)：7-12

[3] TAKAHASHI W.A convexity in metric space and nonexpansive mappings[J].Kodai Math,1970(20)：142-149

[4] GREGUS M.A fixed point theorem in banach spaces[J].Boll Unione Mat Ital Sez A,1980(17)：193 -198

[5] FUKHA H.Fixed point results for a generalized nonexpansive map in uniformly conxex metric spaces[J]. Nonlinear Analysis,2012(75)：4747-4760

[6] JONG S J.Strong convergence of iterative methods fork-strictly pseudo-contractive mappings in Hilbert spaces [J].Applied Mathematics and Computation,2010(215)：3746-3753

Keywords：fixed point；contraction；non-expansion；convex metric space

Fixed Point Theorem of Generalized Non-expansive Mapping

DENGHong-yan

(School of Mathematics, Chongqing Normal University, Chongqing 401331, China)

This paper introduces a kind of mapping from a class of generalized non-expansive mapping, extends the results by Bogin and Gregus, and gives proofs for the fixed point theorem on complete metric space and complete convex metric space.

1672-058X(2013)10-0008-05

2013-04-10；

2013-05-06.

邓红彦(1988-)，女，重庆人，硕士研究生，从事不动点理论及其应用研究

O177

A

责任编辑：李翠薇