水库调洪数值—解析法的研究及其在福安市防洪排涝设计中的应用

李松兴

（宁德市东闽水利水电勘察设计有限公司 福建宁德 352100)

水库调洪演算大多采用试算法、图解法或相关图法。这些水库调洪演算方法大都是通过对相关的水量平衡方程进行图解和求解来实现的，相应的计算工作量大、效率低，在编程灵活性和计算精度等方面也存在一定的局限性。近期水库调洪计算研究的重点是如何找到一种从理论与实用上满足水库在遭遇大洪水，水库实时洪水调度计算所需的高精度、高速度，适合计算机计算使用的调洪计算方法。此方法不用试算，更无需迭代求解。水库调洪数值解析解法就是这样一种调洪计算方法，便于计算机用程序实现。本文从防洪调度方式复杂的水库调洪计算出发，讨论水库调洪计算的主要内容，并探讨基于水库调洪数值—解析解法在福安市湾坞分区西片防洪排涝中的应用。

1 水库调洪数值—解析解法

1.1 水库调洪数值—解析解法原理

复杂情况下水库调洪计算通常有两种不同的求解情况：

（1)已知时刻tn-1的水库水位Zn-1、入库洪水流量Q(tn-1)、泄洪流量S(Zn-1)、水库水面面积F(Zn-1)与时刻 tn的入库洪水流量 Q(tn)，在一定的水库泄洪设备类型、开启宽度(或面积)的条件下，求解时刻tn的水库水位Zn与泄洪流量S(Zn)。设hn为计算步长，hn=tn-tn-1。

(2)已知条件与情况(1)相同，求解水库水位达到某一特殊水位 CR的时刻 tn，tn-1＜tn，hn=tn-tn-1。

根据水库调洪计算的基本微分方程为∶

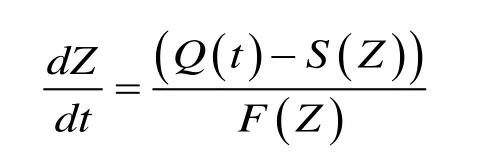
大连理工大学陈守煜教授提出调洪数值解法的四阶龙格—库塔公式为：

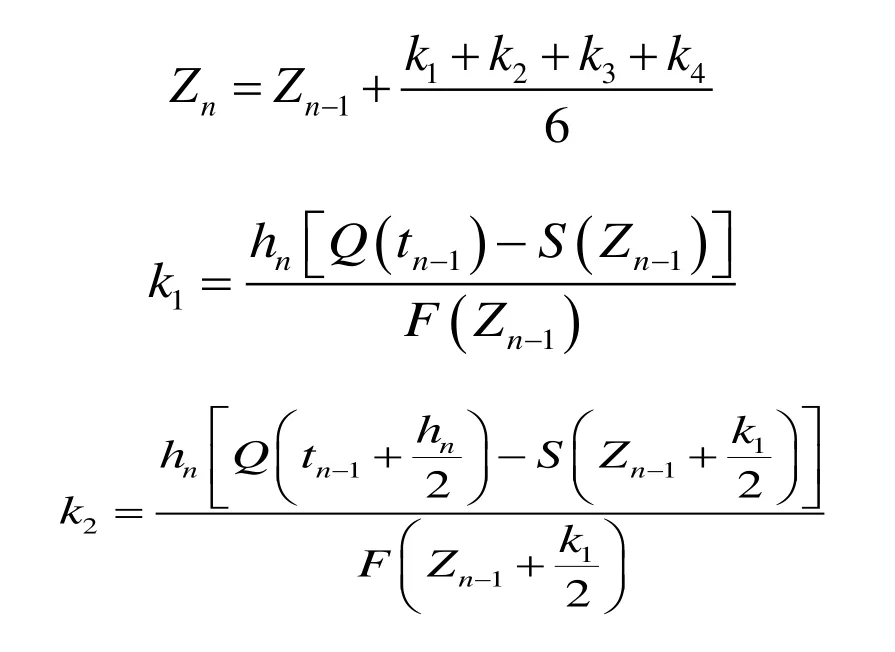
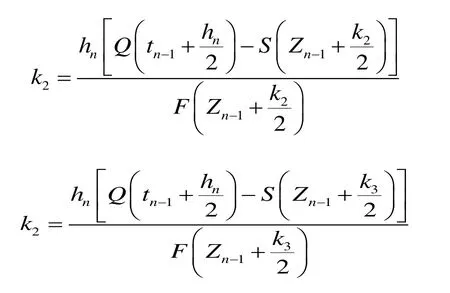
式中：Q(tn-1+hn/2)为时刻tn-1+hn/2的洪水流量；S(Zn-1+k1/2)、S(Zn-1+k2/2)、S(Zn-1+k3)分别为泄洪流量；F(Zn-1+k1/2)、F(Zn-1+k2/2)、F(Zn-1+k3)分别为水库水面面积。

情况(1)可直接用四阶龙格—库塔公式求解。而水库调洪数值—解析解法的基本思路是，对情况（1)的一般计算时段，用四阶龙格—库塔公式，对情况（2)的特殊计算时段用解析法求解，是复杂情况下调洪数值解法的拓展。

考虑到时刻tn-1，tn的入库洪水流量Q(tn-1)，Q(tn)呈线性变化(增长或减少)，则时刻 tn的洪水流量 Q(tn)，可根据线性内插确定，将水库调洪计算的微分方程变换为：

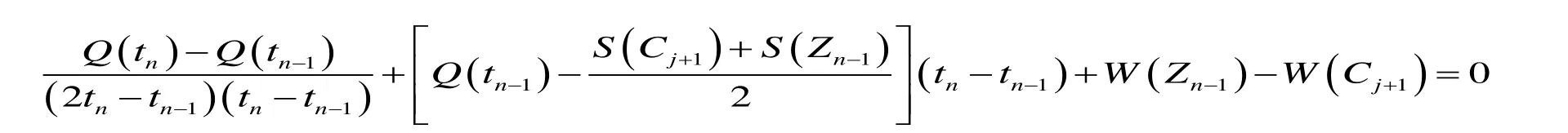
式中：W为水库蓄水量。由二次方程的求根公式解得水库水位达到特殊水位Cj+1的时刻tn的解析式为

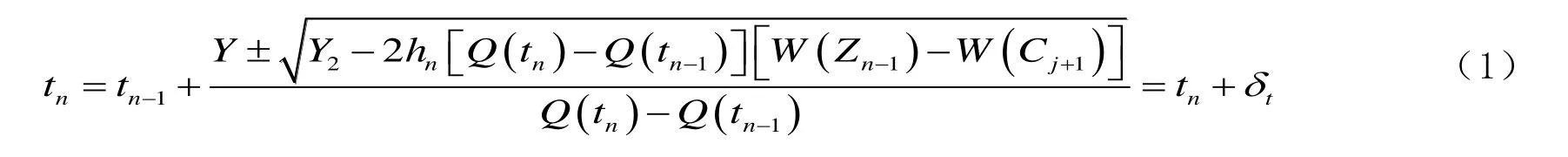
满足 tn-1＜tn，式中：

根据对水库调洪过程的分析可知，确定式（1)根号前取符号的条件是δt> 0且δt＜tn-tn-1。情况（2)可直接根据公式（1)求解，不必试算。计算速度、精度、稳定性与四阶龙格—库塔调洪数值解法相当。

1.2 运用Visual Basic软件编写程序

1.2.1 数据载入

将诸如库容曲线、洪水过程、不同泄洪建筑物及闸门开度对应的泄流曲线等数据赋值给相应的变量来进行计算。

1.2.2 结构模块化

虽然面向对象的编程方法是当今的主流，但对以数值计算为主的程序仍常延用结构化的编程方法，把各个功能的模块分开然后用主程序按需要调用，如插值模块、下泄流量试算模块、洪水演算进程模块等部分，把它们分别写成相对独立的函数体并在主程序里调用。

2 福安市湾坞分区西片防洪排涝的调洪演算

2.1 工程概况

福安市地处宁德中部，位于福建省东北沿海，宁德市境内地形以丘陵山地为主，间以河谷平地和山间盆谷，全市海岸线长878km。

湾坞垦区地面库 20年一遇最高洪水位的确定，考虑两种组合即：（1)20年一遇洪水对应多年平均高潮位；（2)20年一遇高潮位对应于多年平均洪水，然后取这两种组合的外包线。由于湾坞垦区地面库具有一定的调蓄能力，故各垦区地面库内最高水位的确定，必须通过调洪演算才能确定。

洪水主要通过原有的水闸泄入大海，当海潮水位高于滞洪区内水位时闸门关闭挡潮，反之则闸门开启泄流排洪。

2.2 调洪演算

（1)20年一遇洪水对应多年平均高潮位。经调洪演算得各特征值见表1。

（2)20年一遇高潮位对应于多年平均洪水。多年平均年最大24h降雨130mm，3个滞洪区24h降雨总量分别为 26.3、54.1、87.6万 m3，不考虑向外海排泄，全部留在滞洪区内（实际不可能)，此时对应滞洪区内的水位为3.46、3.25、3.02m。小于20年一遇设计洪水对应于多年平均最高潮位调洪后的塘内最高水位3.6m。

根据本地区水文雨潮组合分析，降雨的雨峰与白马港高潮位遭遇的可能性较大，对规划区防洪排涝偏不利。当出现设计重现期降雨时，潮汐高潮位重现期一般为多年平均。因此，规划区洪涝重现期采用相应重现期的降雨与多年平均偏不利潮型组合。防洪工况按 20年一遇设计洪水对应多年平均高潮位。

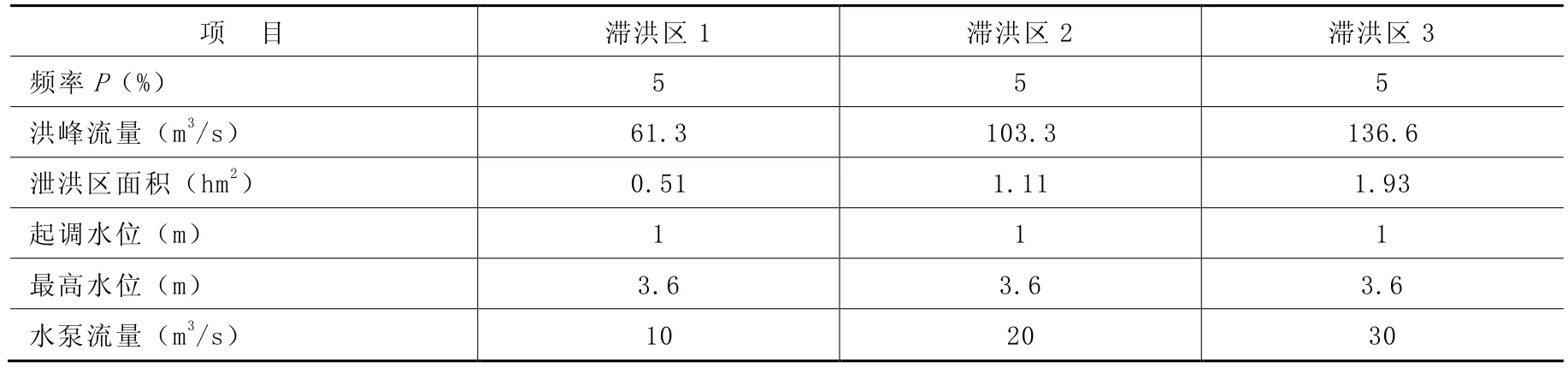
表1 特征值

3 结语

水库调洪数值—解析解法是调洪解法的发展。它将复杂情况下调洪的两种求解情况均用直接方法求解，不必用试算法，更无需迭代求解，从理论与实用上满足了水库在遭遇洪水情况下，水库实时洪水调度计算所需的高速度与高精度的双重要求。它为当前国内外迅速兴起的水库洪水调度自动化系统提供了理论严谨、计算速度快、精度高的复杂情况下水库调洪计算模型。显然，水库调洪数值—解析解法必将广泛应用于全国大中型水库的洪水调节计算。

1 陈守煜.水库调洪数值—解析解法.大连理工大学学报，1996，36(6)：721-724.

2 陈守煜.复杂情况下水库调洪数值解法.大连理工大学学报，1995，35（4)：536-539.

3 李庆扬，王能超，易大义.数值分析〔M〕.华中科技大学出版社，1986.

4 陈守煜.水库调洪数值解析法的理论、模式与程序.重庆交通学院学报，1983(1)：60-69.