梯形明渠水跃共轭水深的精确解

王学斌，张毅

（中国水电建设集团第十五工程局有限公司，陕西西安 710065）

1 梯形断面的水跃共轭水深的研究现状

梯形断面是重要的明渠断面形式之一。在梯形明渠的消力池水力计算中，需要计算水跃的共轭水深。但由于梯形明渠断面形式比较复杂，水跃共轭水深的计算公式为高次方程，求解比较困难，所以在以往的计算中，常采用图解法和试算法[1-2]，图解法计算精度低、试算法计算工作量大。近年来许多学者采用迭代算法[3-8]，迭代计算的优点是比试算法简单、比图解法精度高，缺点是计算精度和收敛速度与迭代公式的形式有关，选取初值比较困难。赵延风[7]比较了各学者迭代公式的精度，认为“冯家涛公式的最大相对误差跃前为－3.287%，跃后为－3.002%；刘玲公式的跃前为－2.122%，跃后为－2.236%；张小林公式的跃前为－6.014%，跃后为9.460%；孙道宗公式的跃前为－14.359%，跃后为－7.737%；赵延风公式的最大相对误差跃前为0.963%，跃后为－1.1%。对于初值的选取，冯家涛和张小林采用的初值均为矩形断面水跃的共轭水深，但张小林在初值的计算公式中引入了断面特征参数β，以提高计算精度；李蕊在跃后水深的迭代计算中，初值选取需解一元三次方程，在跃前水深的迭代计算中，初值选取需解一元二次方程。

刘计良[9]根据水跃函数曲线的性质和几何意义，假设跃前与跃后水深呈双曲线关系，结合梯形明渠临界水深的计算公式，给出了水跃共轭水深的简单计算方法。金菊良[10]把求解梯形明渠水跃共轭水深的问题等价于两个非线性优化问题，采用加速遗传算法计算梯形明渠的水跃方程，遗传算法是一种求解非线性方程的一种优化算法，如果迭代次数足够且不产生局部收敛，其计算值与精确解非常接近。文献[11]给出了水跃共轭水深的精确解，但给出的算例中跃前断面水深与跃后相差不大，跃前断面的弗劳德数小于1，众所周知，跃前断面弗劳德数小于1是不能发生水跃的。

由以上论述可以看出，梯形明渠水跃共轭水深的计算有试算法、图解法、迭代计算和遗传算法。这些算法均为近似计算方法，只有文献[11]给出了梯形明渠水跃共轭水深的精确计算公式，但在其算例中出现了跃前断面弗劳德数小于1的情况，原因不详。因此本研究从梯形明渠的水跃方程以及一元四次方程的解法，给出梯形明渠水跃共轭水深比的精确计算公式。

2 梯形明渠的水跃共轭水深比

梯形渠道的水跃方程根据其推导方法不同，有不同的形式，可以化为一元五次方程，也可以简化为一元四次方程。

文献[1]给出了梯形断面的水跃方程为

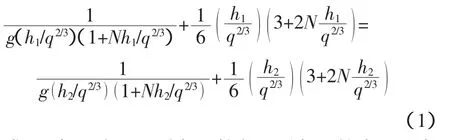
式（1）中，h1和h2分别为跃前和跃后断面的水深；g为重力加速度；q=Q/b为虚拟的单宽流量；Q为流量；b为梯形渠道的底宽；N=mq2/3/b；m为梯形断面的边坡系数。对上式进一步推导可得

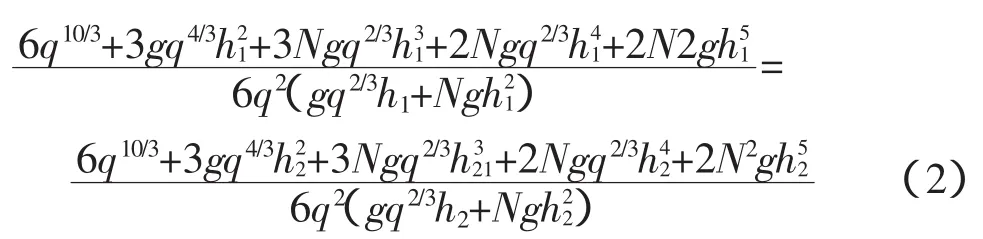
由式（2）可以看出，梯形断面的水跃方程为五次方程，不易求解。

文献[12]给出的梯形渠道水跃方程为四次方程，该方程为

式（3）中，β=b/（mh1）；η=h2/h1；σ2=Q2/（gm2h51）。

文献[13]对公式（3）进行了详细的推导，证明了公式（3）的正确性。公式（3）为一元四次方程，可以根据一元四次方程的解法，给出梯形断面明渠水跃方程的精确解。因为

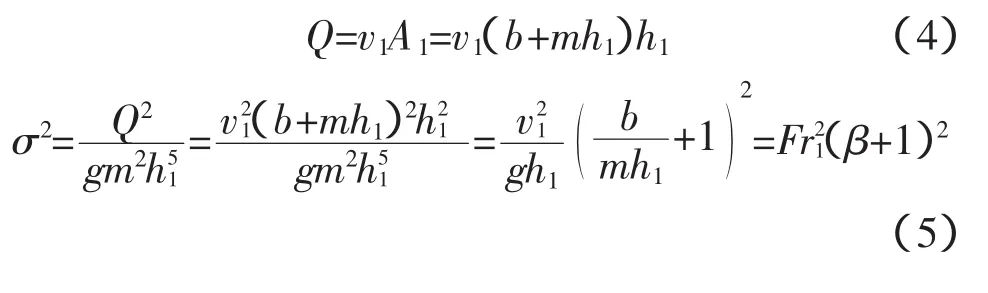
式中，v1为跃前断面的平均流速称为跃前断面的弗劳德数。将公式（5）代入公式（3）得

如果知道跃后水深h2，仍可由上式求解h1，方程为

式中，v2为跃后断面的平均流速

公式（6）和（7）均为一元四次方程，可以根据一元四次方程求根的方法来求解。

一元四次方程的标准形式为[14]

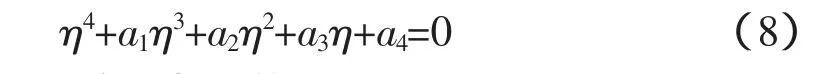
式中，a1、a2、a3和a4为系数。

对比公式（6）和公式（8）得

根据文献[15]介绍的费拉里一元四次方程的解法，公式（8）可以写成

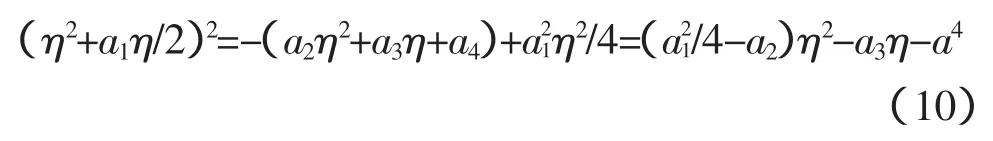
引入t得

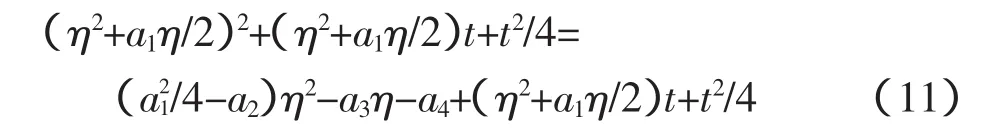
公式（11）可以写成

公式（12）的右边为一元二次方程，为了使公式（12）的右边变成完全平方式，使其判别式

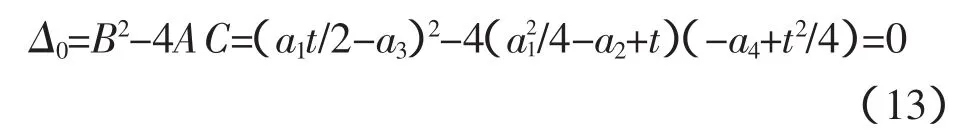
由上式解出t

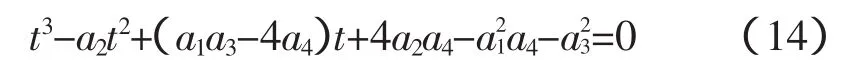
令t=y+a2/3，公式（14）化为

公式（15）为一元三次方程，根据卡丹公式，当Δ=（q0/2）2+（p0/3）3>0时，方程有一个实根和两个虚根，当Δ=（q0/2）2+（p0/3）3<0时，方程有三个不等的实根，当Δ=（q0/2）2+（p0/3）3=0时，方程有三个实根，其中至少有两个相等的实根。对于梯形断面水跃共轭水深比，一般可能会出Δ=（q0/2）2+（p0/3）3>0和Δ=（q0/2）2+（p0/3）3<0两种情况，由此可以得到

当Δ=（q0/2）2+（p0/3）3>0时

如果已知跃前断面水深h1，求跃后断面水深h2，由水跃的性质可知，共轭水深比应取大值，所以有

因为跃前和跃后水深为共轭水深，如果已知h2求h1，仍可用公式（23）计算。

3 公式比较

为了比较各学者公式的精度，现用一工程实例进行验证。已知梯形断面的底宽b=7 m，边坡系数m=1，渠道通过的流量分别为4.10、45.84、129.64、366.68、673.64和1037.14 m3/s。工程常用范围内的N=mq2/3/b=0.1~4.0，用本文公式（23）的精确解与各学者的迭代公式比较如表1所示。由表中可以看出，刘玲公式计算的误差最小，在所取的误差精度范围内误差均为零（刘玲曾将86组数据的迭代计算值与精确解比较，相对误差为0~1.01%）；刘计良的公式误差最大，范围在0.677%~17.4%；其余学者的公式误差不大，其值在0.013%~2.312%。由此可以看出，本文提出梯形断面水跃共轭水深的精确解为水跃的一般解，具有普适性，而其他计算方法存在不同程度的误差。

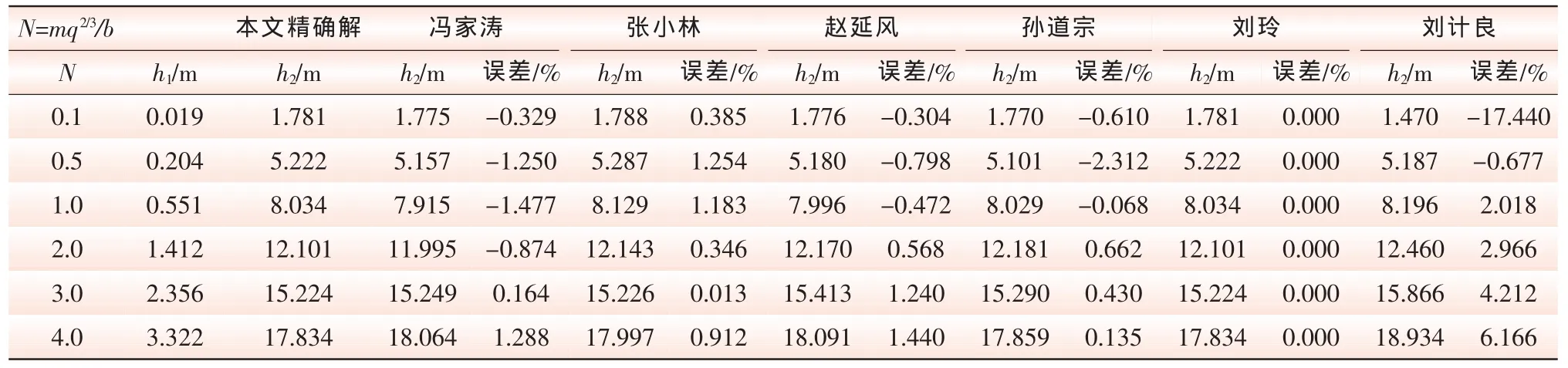
表1 本文精确解与各学者迭代公式计算结果比较Tab.1 Comparisons between the exact solution of this paper and each scholar iterative formula

4 解题步骤

1）根据已知的参数β或β0，由公式（9）确定系数a1、a2、a3、a4。

2）求一元三次方程的系数p0和求q0。

3）求判别式Δ=（q0/2）2+（p0/3）3。

4）Δ=（q0/2）2+（p0/3）3>0，由公式（16）求y；Δ=（q0/2）2+（p0/3）3<0，由公式（18）求y。

5）求t=y+a2/3。

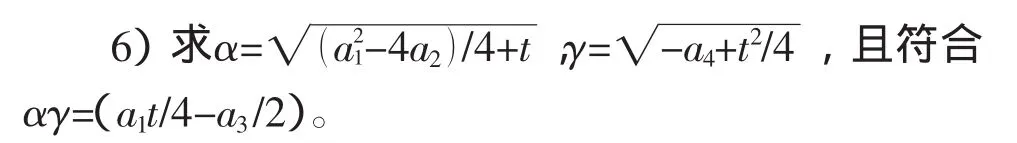
7）由公式（23）求共轭水深比。

8）求跃后水深h2=ηh1或跃前水深h1=η0h2

算例1:有一梯形断面明渠，通过的流量Q＝54.3 m3/s，底宽b＝7 m，边坡系数m＝1，渠道中发生水跃，已知跃前水深h1＝0.8 m，试求跃后水深h2。

解：为了求解方便，现列表计算，见表2。

如果已知跃后水深h2＝3.0038，求跃前水深h1，计算过程如表3所示。

算例2：已知某梯形渠道的β=b/（mh1）=40，Fr21=1.523，求梯形渠道水跃的共轭水深比η。

解：列表计算，见表4。

表2 跃后水深h2计算表Tab.2 Calculation table of water depth after the hydraulic jump h2

表3 跃前水深h1计算表Tab.3 Calculation table of water depth after the hydraulic jump h1

表4 梯形渠道水跃的共轭水深比η计算表Tab.4 Calculation table for trapezoid open channel hydraulic jump conjugate depths ratio η

5 结语

梯形断面明渠水跃共轭水深计算公式比较复杂，目前尚没有显式计算方法，多采用试算法、图解法或迭代计算，计算过程复杂，初值选用困难，计算精度较低。本文通过解一元四次方程，给出了梯形断面明渠水跃共轭水深的显式精确解，比试算法、图解法和迭代法方便，简单，使水跃共轭水深的计算具有普适性，可供工程设计参考。

[1] 吴持恭.水力学[M].北京：高等教育出版社，1998：338-347.

[2] 清华大学水力学教研室，水力学[M].北京：高等教育出版社，1982：94-95.

[3]冯家涛.梯形渠道水跃共轭水深直接计算公式[J].力学与实践，1998，20（5）:50-53.FENG Jia-tao.A direct calculation formula for conjugate water depth of water jump in a trapezoid channel[J].Mechanics in Engineering，1998，20（5）:50-53（in Chinese）.

[4] 张小林，刘惹梅.梯形断面渠道水跃共轭水深的计算方法[J].水利与建筑工程学报，2003，1（2）:41-43.ZHANG Xiao-lin，LIU Re-mei.Method of calculation for conjugate water depth of water jump in trapezoid channel[J].Journal of Water Resources and Architectural Engineering，2003，1（2）:41-43（in Chinese）.

[5]刘玲，刘伊生．梯形渠道水跃共轭水深计算方法[J].北方交通大学学报，1999，23（3）:44-47.LIU Ling，LIU Yi-sheng.Calculating method for conjugate depth of hydraulic jump in trapezoidal channels[J].Journal of Northern Jiaotong University，1999，23（3）:44-47（in Chinese）.

[6] 李蕊，王正中，张宽地，等.梯形明渠共轭水深计算方法[J].长江科学院学报，2012，29（11）:33-36.LI Rui，WANG Zheng-zhong，ZHANG Kuan-di，et al.Calculation method for conjugate water depth in open trapezoidal channel[J].Journal of Yangtze River Scientific Research Institute，2012，29（11）:33-36（in Chinese）.

[7] 赵延风，王正中，芦琴，等.梯形明渠水跃共轭水深的直接计算方法[J].山东大学学报：工学版，2009，39（2）:131-136.ZHAO Yan-feng，WANG Zheng-zhong，LU Qin，et al.Direct calculation method for conjugate water depth of the trapezoidal open channel[J].Journal of Shandong University:Engineering Science，2009，39（2）:131-136（in Chinese）.

[8]孙道宗.梯形断面渠道中水跃共轭水深计算[J].江西水利科技，2003，29（3）:133-137.SUN Dao-zong.The calculation of the conjugate depth about the hydraulic jump of the canal of the trapezoidal section[J].Jiangxi Hydraulic Science&Technology，2003，29（3）:133-137（in Chinese）.

[9] 刘计良，王正中，杨晓松，等.梯形渠道水跃共轭水深理论计算方法初探[J].水力发电学报，2010，29（5）:216-219.LIU Ji-liang，WANG Zheng-zhong，YANG Xiao-song，et al.Preliminary study on the theoretical method for calculating conjugate depth of trapezoidal channel[J].Journal of Hydroelectric Engineering，2010，29（5）:216-219 （in Chinese）.

[10]金菊良，付强，魏一鸣，等.梯形明渠水跃共轭水深的优化计算[J].东北农业大学学报，2002，33（1）:58-62.JIN Ju-liang，FU Qiang，WEI Yi-ming，et al.Optimal computation for conjugate water depth of hydraulic jumps in trapezoidal channels[J].Journal of Northeast Agricultural University，2002，33（1）:58-62（in Chinese）.

[11]王兴全.梯形明渠水跃共扼水深的计算[J].农田水利与小水电，1989（9）:16-18.WANG Xing-quan.Computation for conjugate water depth of hydraulic jumps in trapezoidal channels[J].Rural Water and Hydropower，1989（9）:16-18（in Chinese）.

[12]余常昭.明槽急变流[M].北京：清华大学出版社，1999：94-95.

[13]张志昌.水力学习题解析：下册[M].北京：中国水利水电出版社，2012：54-55.

[14]王连祥.数学手册[M].北京：高等教育出版社，1999:87-90.

[15]郭敏.一元四次方程公式解的追根溯源[J].数学之友，2011（12）:72-73.GUO Min.Tracing the source of the solution of quartic equation formula[J].Company in Mathematics，2011（12）:72-73（in Chinese）.