高精度陶瓷砖平整度检测系统

胡尧俊，郭峰林，田 魁

(武汉工业学院数学与计算机学院，湖北武汉 430023)

随着经济的发展和人们生活水平的提高，中国已然成为陶瓷砖生产大国，陶瓷企业在整个国民经济中的地位也越来越重要。但与陶瓷墙地砖现代化生产工艺相比，国内墙地砖产品的检测技术与检测设备仍明显滞后。目前，虽然国内已经研制出了一些陶瓷砖平整度检测系统，很多工厂也已不再使用传统的人工抽样和手工检测的方法，但就整体而言，国内陶瓷砖检测装备与检测仪器仍无法满足陶瓷砖表面平整度检测的精度及自动化的要求。而从国外引进的检测设备，又由于与我国的陶瓷砖生产中陶瓷生产企业的自动化程度不高、成品质量不稳定、且对尺寸分拣精度要求较高的具体状况不相符而没有很大的实用价值［1］。因此，设计一套高精度、智能化、经济化、非接触化的陶瓷砖平整度检测系统具有非常重要的现实意义。

本文中通过自行设计的数据采集模块、数据处理模块，设计了一套高精度陶瓷砖平整度检测系统，通过高精度的硬件采集模块和合适的软件滤波处理方法、平整度计算方法，使本检测系统既可以适应我国陶瓷砖生产企业的现状要求又可达到高精度的要求。

1 系统结构

如图1所示，本检测系统主要由数据采集模块、数据传输模块、数据处理模块、系统控制模块和人机交互模块五部分组成。

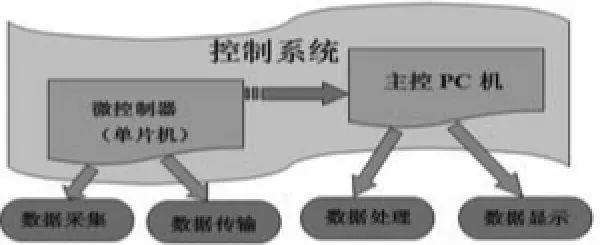
图1 系统功能模块图

其中数据采集模块主要由精密激光位移传感器CD33、16位A/D转换器TLC4545等硬件元件组成，用以实现数据的采集和模/数转换;数据传输模块主要通过对SPI和RS－232总线的设定来实现数据的传输;系统控制模块主要由单片机微控系统和PC机主控系统构成;数据处理模块主要涉及数据的滤波算法及平整度计算算法，最后由人机交互界面显示检测结果。系统结构图如图2所示。

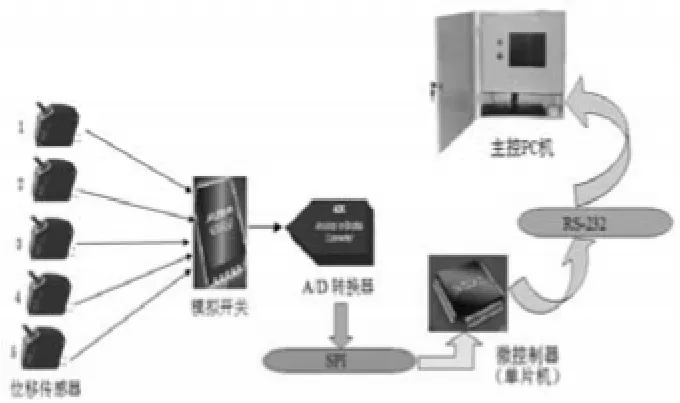
图2 平整度检测系统结构图

2 平整度检测算法

2.1 国家标准算法

根据GB/T3810.2-2006中的相关规定，瓷砖平整度主要涉及3项评定指标:中心弯曲度、边弯曲度和翘曲度。其中，中心弯曲度指瓷砖中心点偏离由4个角点中的三点所确定的平面的距离;边弯曲度是指瓷砖的一条边的中点偏离2个端点所确定的直线的距离;翘曲度指由瓷砖的3个角点确定一个平面，第4个角点偏离该平面的距离［2］。图3所示为国家标准算法中特征点分布图。

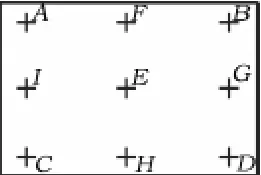
图3 国家标准算法特征点分布图

在瓷砖平整度在线检测过程中，激光位移传感器的直接测量值是传感器到瓷砖表面的距离。在在线测量过程中，能否准确获取这个距离对于瓷砖平整度的检测结果有较大的影响［3］。

2.2 企业标准算法

然而在实际生产中，长年以来工厂惯常使用的检测方法则是直接用垂直检测尺(靠尺)测量瓷砖四条边、对角线及中线的边直度，以此来作为对瓷砖平整度的判断依据。

综合国家标准和企业标准两种算法，为了使所设计的检测系统具有更好的科学性和实用性，本设计选择对瓷砖平整度所涉及的以下3个方面的评定指标进行检测，即边弯曲度、中心弯曲度和对角弯曲度。图4、图5为在瓷砖表面所设检测点的位置分布图。以A点坐标(0，0，ZA)为基准，在三维坐标中分别确定其他各点的坐标。

图4 边弯曲度检测点

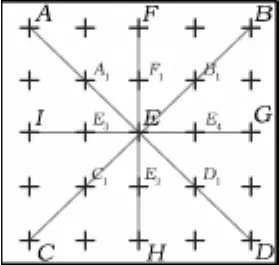
图5 中心弯曲度、对角弯曲度检测点

设各点坐标分别为:

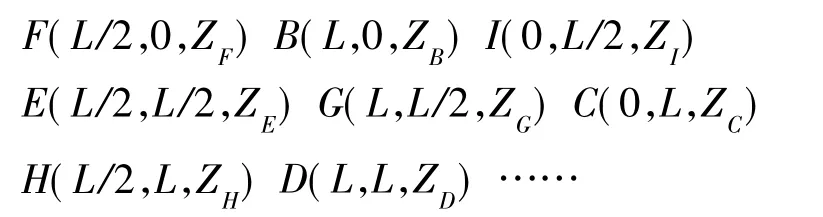
边弯曲度指一条边中间三点到该边两端点所连直线的距离，取三个距离中的最大值就是该边的边弯曲度。以AB边为例，就是指F、F1、F2三点在空间中到直线AB的距离，取三个值中的最大值，即为AB边的边弯曲度。

设直线AB在空间坐标系中的方程为:aX+bY+cZ=n(n为常数)，由空间中点到直线的距离公式:

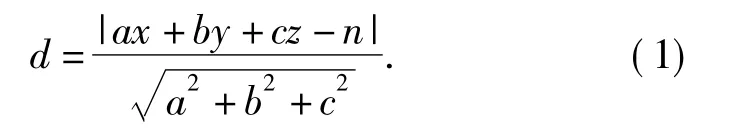
可以求出点F、F1、F2到直线AB的距离dF、dF1、dF2，AB 边弯曲度即为 dL=max{dF，dF1，dF2}。

AC、CD、DB边的边弯曲度同理可求。

图5中，中心弯曲度指边FH、GI中间三点到该边两端点所连直线的距离的最大值，即点E1、E、E2(E3、E、E4)到直线FH(GI)空间距离的最大值。设点E1、E、E2(E3、E、E4)到直线FH(IG)空的间距离分别为dE1，dEFH，dE2(dE3，dEGI，dE4)。令:

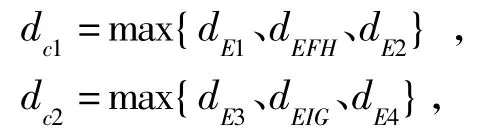
则中心弯曲度dc=max{dc1、dc2}。

对角弯曲度指的是对角线AD、BC中间三点到该边两端点所连直线的距离的最大值，即点A1、E、D1(B1、E、C1)到直线AD(BC)空间距离的最大值。令:

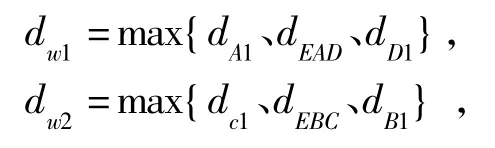
则对角弯曲度dw=max{dw1、dw2}。

3 滤波算法

在工厂的实际生产中由于大的电流开关、变压器、电磁继电器以及各种电器设备的存在，使得在信号的采集、传输过程中经常会出现各种电磁干扰，其中以50 Hz工频干扰最为严重，因此在对数据进行计算之前需要对其进行滤波处理。

到目前为止已经出现了很多种滤波算法，例如较早提出的Wiener滤波、Kalman滤波、和自适应滤波，但它们都是线性滤波，会在滤除噪声的同时造成信号边缘的模糊，因此本系统选择一种非线性滤波算法——中值滤波算法，实现对数据的滤波处理。

中值滤波是一种典型的非线性滤波方法，它是建立在最小绝对误差准则之上的最佳滤波方法。其运算简单，在滤除脉冲噪声的同时也可以很好地保护信号的细节信息。特别的，它可以克服由仪器外部环境偶然因素引起的突变性扰动或仪器内部不稳定引起误码等造成的尖脉冲干扰。

中值滤波的定义如下:

首先取一长度为L=2N+1的滤波窗口(N为正整数)，设在第n时刻输入信号序列在窗口内的样点为x(n －N)，…，x(n)，…，x(n+N)。

此时中值滤波的输出为:

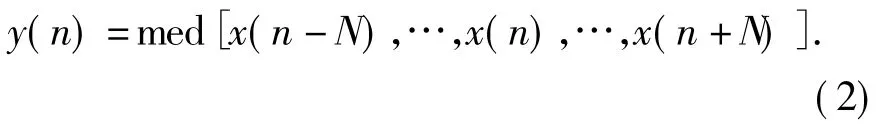
其中，med［］表示窗口内所有的数按从小到大的秩序排列后，取其中值的运算［4］。

滤波前后的波形图如图6、图7所示。

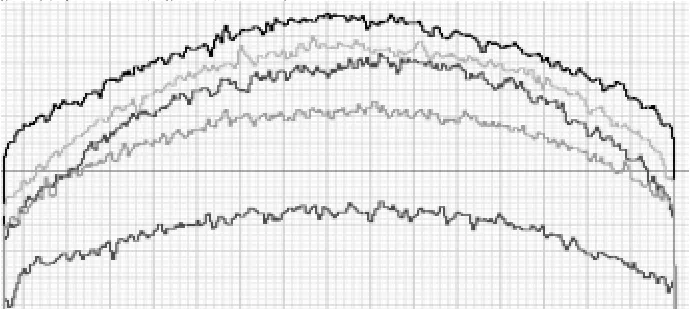
图6 滤波前的波形图

图7 滤波后的波形图

此时中心线高度为47.6 mm，显示范围为(+/－)1.0 mm，垂直像素为0.003 3 mm。

由图6、图7可知，所选用的中值滤波算法具有较好的滤除噪声的能力。

4 实验结果及系统标定

系统组建完成后，需要对系统进行测试，以保证检测系统的可靠性和稳定性。

4.1 位移传感器水平位置的标定及数据误差的补偿

在安装传感器时，为了减小由于5只传感器没有安装在同一水平面上而引入的系统误差，需要对系统中传感器的高度进行标定。本设计中的标定方法是:将一把具有一定高度视为具有理想平面的垂直检测尺(靠尺)放在位移传感器的检测范围内，由5只传感器同时对其正下方的5个点的高度进行检测。若5个传感器所测的高度值之间的差距在误差允许范围内，则说明5个传感器安装的高度误差在允许范围之内，系统所测数据可靠;若高度误差超过允许范围，则应重新调整各个传感器的位置，再次标定，直到符合标准为止。传感器高度标定的波形图如图8所示。

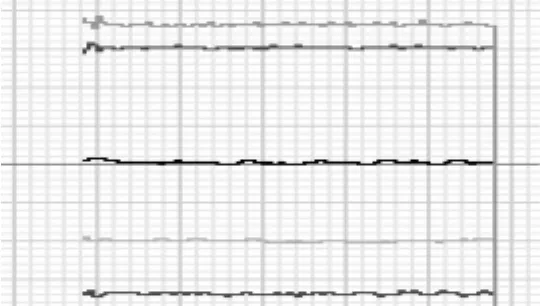
图8 传感器高度标定的波形图

此时中心线高度为47.7 mm，显示范围为(+/－)0.5 mm，垂直像素为0.001 7 mm。

由图8可直观看出，每个传感器自身在不同时间所测高度值基本在同一数值上，可见各个传感器在采集数据时具有较高的稳定性，且在5个传感器之间，2号和3号之间高度差最大，其最大距离差:

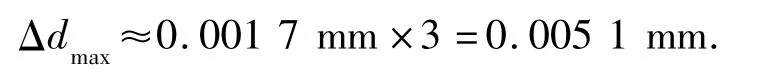
该误差在允许范围之内。

以3号传感器所采集的数据为基准，可以求得1，2，4，5号传感器所采集的数据与其差值，设为Δd13、Δd23、Δd43、Δd53，这些差值可以在进行平整度计算时对数据进行补偿，以进一步减小误差、提高精度。

4.2 系统重复性检测及实验数据分析

在检测系统正式运行前需要对其准确性和重复性进行检测。

由测量实践可知，在排除了系统误差和粗大误差的情况下，对某一物理量进行等精度的多次测量时，其测得值中还会含有随机误差。随机误差的数字特征主要有两个:算术平均值和均方差。前者通常是随机误差的分布中心，后者则是分散性指标［5］。

设x1，x2，…，xn为n次测量所得的值，则算术平均值为:

多次测量所得的测得值是以算术平均值为中心而集中分布的，因此算术均值可以作为等精度多次测量的结果。

n次测量的均方差σ为:

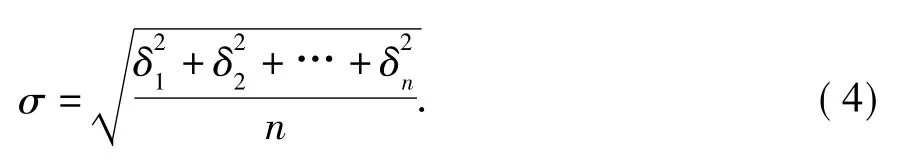
均方差可以描述随机误差的散布范围，均方差越小，测得数据的分散范围也越小，因此均方差可以用来评定测量值的精度。

由以上的分析可设计本系统的检验的方法是:通过该检测系统对一块经过人工测量的样本瓷砖的平整度进行30次重复检测，计算30次检测数据的均值和均方差。若系统检测的数据均值与人工测量的数据差值在误差范围之内，则说明该系统具有较高的准确度;若30次重复测量值的标准差在误差范围之内，则说明系统具有良好的重复性，能够满足实际检测的需要。实验数据如表1所示。

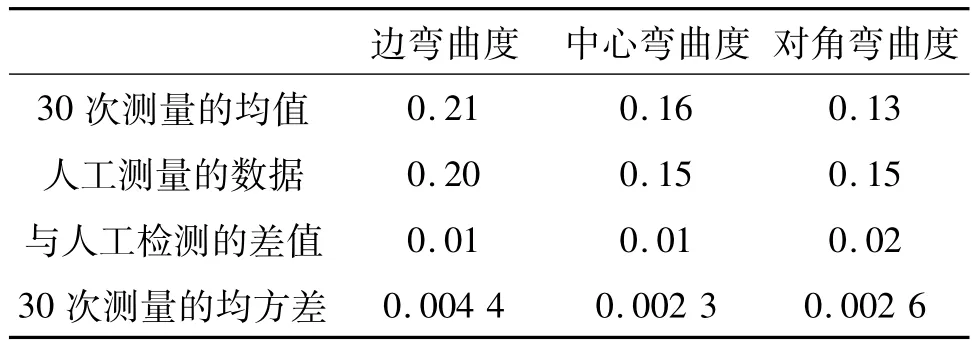
表1 系统实验检测数据 /mm

由表1中实验数据可知，系统重复测量的均值与人工测量值之间的差值小于等于0.02 mm，重复测量数据的均方差的最大值为0.004 4，因此可以认为所设计的平整度检测系统的检测误差在允许范围之内，系统准确度和精度均达到预期设计要求，该系统具有较高的准确性和稳定性。

5 结束语

本文设计了一套高精度陶瓷砖平整度在线检测系统。该系统通过自行设计的数据采集模块、数据滤波及平整度计算模块，最后由实际检测结果证明该系统的检测精度可以达到0.02 mm的预期要求。该系统通过华南精密仪器研究院的实际检验测试，证明在实际生产环境中也可以达到较好的效果。

［1］许江.陶瓷墙地砖平整度在线检测系统研制［D］.杭州:浙江大学，2006.

［2］GB/T 3810.2－2006，陶瓷砖试验方法.第二部分:尺寸和表面质量的检验［S］.

［3］尤波，王伟，许家忠.基于PLC的瓷砖平整度在线检测系统研究［J］.自动化技术与应用，2012，31(3):64－68.

［4］王欣，王德隽.离散信号的滤波［M］.北京:电子工业出版社，2002.

［5］梁晋文，陈林才，何贡.误差理论与数据处理［M］.北京:中国计量出版社(第二版)，2001.