非线性静力分析的分段计算法
赵 峰,宋少云
(武汉工业学院机械工程学院,湖北武汉 430023)
在对某铝合金材料汽车手刹进行有限元分析过程中出现了应力超过了铝合金屈服极限的情况,即材料发生了弹塑性变形,在此情况下传统的计算方法直接将外力载荷平均分为若干段,逐步增加载荷后进行计算,这种计算方法耗时太长。
为了解决这个问题,本文提出了分段计算法。将计算分段为两个载荷步。第一个载荷步内把屈服极限之前的计算当作线性行为,只划分一个载荷子步;第二个载荷步,对于超过屈服极限的部分,划分为多个载荷子步计算。经过研究表明,相对传统计算方法而言,该法计算精度基本相当,而计算效率提高了67%。
1 材料非线性的有限元解法
大多数工程实际中,实际结构的位移与载荷是呈非线性关系的,这样的体系称为非线性变形体系。如果体系的非线性是由于材料应力与应变关系的非线性引起的,则称为材料非线性,如材料的弹塑性、松弛、蠕变等。如果结构的形状、位置使体系的受力发生了显著的变化,以至不能采用线性体系的分析方法时就称为几何非线性,如结构的大变形、大挠度等。还有一类非线性问题是边界条件非线性,或接触非线性,如各种接触问题等。本文只讨论材料非线性问题的有限元解法。
材料非线性问题的处理方法[1],通常不必修改整个问题的表达式,而只需将应力—应变关系线性化,求解一系列的线性问题,并通过某种校正方法,最终将材料特性调整到满足给定的本构关系,从而获得问题的解。
非线性问题用有限元法离散化得到如下形式的一组代数方程[1]:
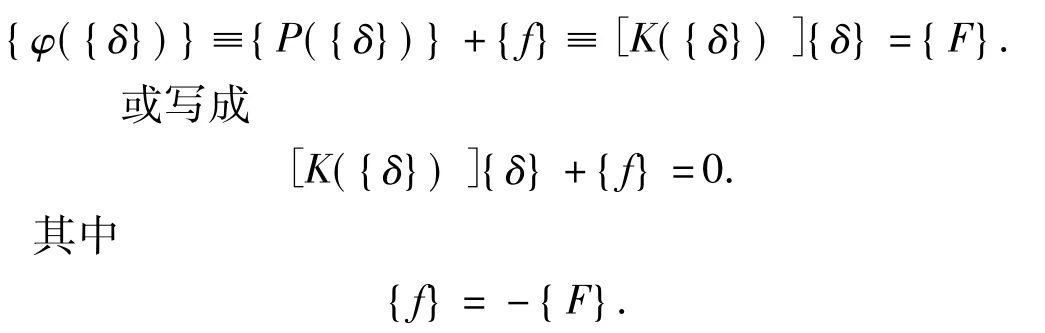
虽然线性方程组[K({δ})]{δ}+{f}=0直接求解并无困难,但对于方程组,单元刚度矩阵是单元节点位移向量的函数,直接求解就行不通。非线性方程组的解法有很多,例如,Newton—Raphson法、增量法、Euler法、混合法等,基本思想都是以反复地进行迭代求解线性方程组去获得满足一定精度要求的非线性方程组的解[2]。
Newton—Raphson算法以增量形式逐渐施加载荷,在每一个载荷增量中完成平衡迭代来使得增量求解达到平衡。在每次求解前NR算法估算出残差矢量,这个矢量是回复力(对应于单元应力载荷)和所加载荷的差值,然后使用非平衡载荷进行线性求解,并且检验收敛性。如果算出的结果不满足收敛准则,重新估算非平衡载荷,修改刚度矩阵,获得新的解。持续进行这种平衡迭代,使该问题得到收敛,如图1所示。

一直进行迭代,直到{F}-{Fur}在允许误差范围内。

图1 Newton—Raphson算法
2 分段计算法的基本思想
对于非线性求解一般有三个操作递进级别:载荷步、子步、平衡迭代[3]。假定载荷在载荷步内是线性变化的,在给定时间范围内直接进行载荷步计算;每一个载荷步的子步内,通过子步或者时间步的逐步加载可以控制ANSYS内部程序来执行多次求解;每一个子步内,将进行一系列的平衡迭代获得收敛的解。为了达到更好的精度,需要设置更多的子步,这导致花费的分析时间也随之而增加。所以在设置更多的子步时,需要考虑精度和时间之间的平衡。ANSYS内部程序通过两种方法控制子步数,第一种是指定子步数或者指定时间步长;第二种是自动时间步长。一般的计算方法是将施加的载荷进行均分,每次缓慢的增加一定载荷,直到达到最终的载荷值。这种方法虽然精度较高,但需要分成很多的子步进行计算,需要分析的时间很长。
本文提出用分段计算法来提高计算效率[4]。该算法适用于应力超过了材料的屈服极限的情况。通过线性计算初步确定到达屈服极限的载荷值,将这个载荷值作为分界点。从零到分界点这个过程,材料没有发生塑性变形,进行线性分析,载荷步分为一个子步;从分界点到最终的载荷值,这个过程材料发生了塑性变形,将载荷进行均分,设置为多个子步,每次缓慢增加一定的载荷,直到最终的载荷值。这种方法迭代次数比一般的方法少很多,计算速度也相应的提高[5]。
3 分段计算法的实例分析
下面以某公司汽车手刹为例来进行静力分析,在保证计算结果精度相同的情况下,比较两种不同分步载荷计算方法。
室温中,手刹在低位的时候对操作臂施加1 200 N的力,操作臂和基座分别为铝合金材质,其他部件均为普通钢材。已知铝合金的屈服极限为80 MPa。具体分析步骤如下。
(1)打开Ansys Workbench建立项目示意图,对手刹进行静力分析。
(2)导入模型:为方便分析,将重要结构部件留下,其他部件抑制,对模型进行简化,将简化后的模型导入workbench,如图2所示。
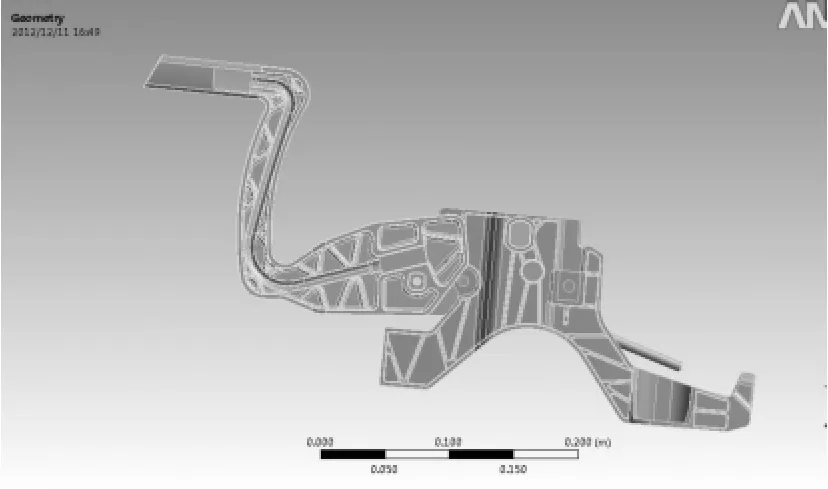
图2 手刹模型
(3)设置材料属性,将操作臂和基座设置为铝合金材质,其他部件均设置为结构钢材质,由于分析过程中发生了材料非线性情况,添加非线性选项,输入铝合金材料曲线数据,如图3所示。

图3 铝合金材料曲线
(4)设置各零部件之间的关系,查看导入模型的连接关系,修改并完善连接方式,整个手刹总共有8个零件:操作臂、基座、两个衬套、传动板、轴、连接螺钉、拉杆。接触方式分为绑定和转动副连接,其中绑定连接有:操作臂和衬套,操作臂和拉杆,基座和轴,基座和连接螺钉,操作臂和连接螺钉:转动副连接有:轴和衬套,传动版和拉杆。
(5)划分网格,使用默认方式进行网格划分,最后划分结果为节点数249 221,单元数146 323。
(6)施加边界条件:将手刹的底面固定;沿着拉杆的轴向方向施加位移为0;对操作臂上表面施加垂直向下的1 200 N的力。
(7)载荷步和时间步长设置
第一种均匀分步载荷的方法[6],在Ansys中对手刹进行设置后,将Analysis Settings打开,Number of steps设置为1,关闭Auto time stepping(自动时间步长),将Substep(子步数)设置为120,也就是将施加在手刹上的力均匀的分隔为120份,以每10N进行加载的方式计算.
第二种二分分步载荷的方法,经过计算,施加载荷为800 N的时候达到铝合金的屈服极限,所以将计算分为两步,第一阶段为0到800 N,直接进行计算;第二阶段为800 N到1 200 N,每10 N进行加载的方式计算。将Analysis Settings打开,Number of steps设置为2,关闭Auto time stepping自动时间步长,将第一步的 Substep(子步数)设置为1,将第二步的Substep(子步数)设置为40。
上面两种计算方法最大应力均发生在操作臂上(见图4、图5),一般方法计算得到最大应力为388.4 MPa,分段计算法计算得到的最大应力为392.3 MPa,且在ANSYS经典界面中,查看最大应力均发生在998节点上。所以由此得到的计算结果,精度基本一致。
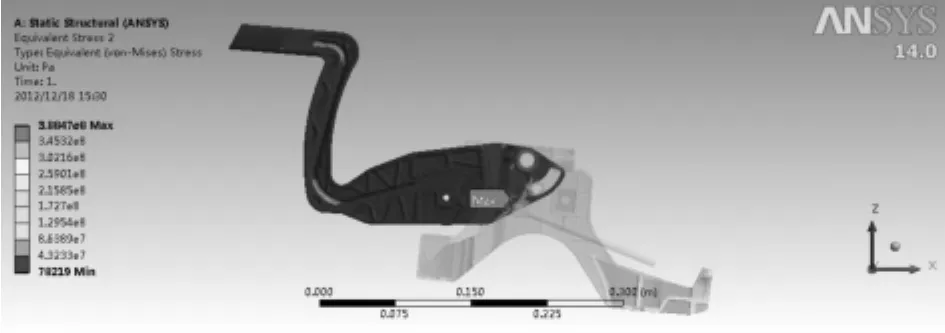
图4 一般计算法最后时刻操作臂应力云图
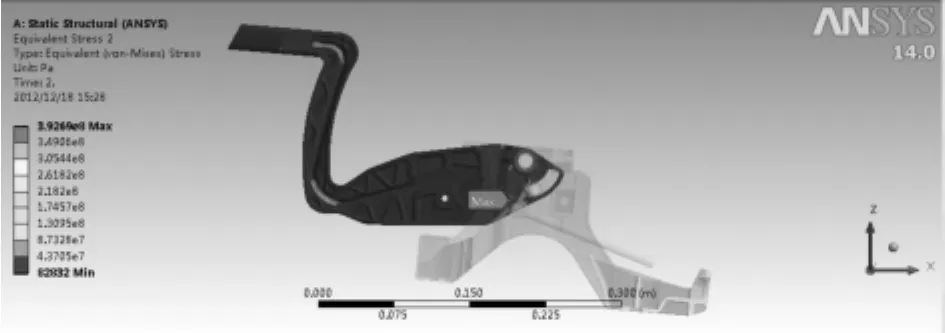
图5 分段计算法最后时刻操纵臂应力云图
为了考察分段计算法的计算精度,这里选取最后时刻应力最大的点(危险点,编号是998),并对两种情况下其应力随载荷变化的历程曲线进行对比(见图6),这两条曲线的误差所绘制的曲线,如图7所示。

图6 危险点的应力的时间历程曲线对比图

图7 危险点两种计算方法的误差曲线
为了查看其它点的情况,这里在操作臂上任选一个点,按照998号点同样的方式绘制出两个曲线图(分别见图8和图9)。

图8 任意点的应力的时间历程曲线对比图

图9 任意点两种计算方法的误差曲线
从上述四个图可以发现,分段计算方法和一般计算方法后半段基本重合,而应力的误差基本可以忽略不计。分段计算法在外力0到800N过程中,用“一步”计算,而一般计算方法用了80步计算,省去了前面的计算步数,节省了分析计算的时间。也就是说在保证计算精度的前提下,分段计算方法提高了计算效率。
经过对比:传统的计算方法分析计算的最大应力388.4 MPa发生在操作臂上,分析所用时间280 min;分段计算法分析计算的最大应力392.3 MPa也发生在操作臂上,分析所用时间120 min;在保证精度相同的情况下,分段计算法将时间效率提高了67%。
[1]殷有泉.非线性有限元分析基础[M].北京:北京大学出版社,2007.
[2]郝好山,胡仁喜,康士延,等.ANSYS LS-DYNA非线性有限元分析从入门到精通[M].北京:机械工业出版社2010.
[3]张洪武,关振群,李云鹏,等.有限元分析与CAE技术基础[M].北京:清华大学出版社,2004.
[4]陈欣,李铀.塑性力学新方法的有限元算法[J].科技信息,2010(13):77 -82.
[5]张俊峰,郝际平,王连坤.几何材料非线性分析的新空间梁柱单元[J].土木建筑与环境工程,2009(3):55-60.
[6]胡玉梅,邓兆祥,王欣,等.汽车后悬架的非线性有限元分析[J].重庆大学学报(自然科学版),2003,26(4):23 -27.

