基于成对约束扩展的半监督网络流量特征选择算法*
李平红,王 勇,陶晓玲
(桂林电子科技大学计算机科学与工程学院,广西桂林 541004)
0 引言
网络流量分类是指在基于TCP/IP协议的Internet中,按照网络的应用类型(例如:WWW,FTP,SMTP,P2P等),将网络通信产生的双向TCP流或UDP流进行分类[1]。准确的网络流量分类是网络流量监控、网络入侵检测和用户行为分析等研究工作的基础。网络流量特征选择是流量分类的关键,它从大量候选特征中删除无关或者冗余的特征,降低候选特征维数,加速分类器建立,直接影响分类的速度和精度。
根据是否使用标记样本作为监督信息,网络流量特征选择算法可以分为有监督学习和无监督学习[2],许多特征选择算法需要大量的标记样本,但已标记样本的获得往往需要专业人士的手工劳动,数量少,提供的信息有限。事实上,监督信息除了类标记样本,还可以是样本间的成对约束[3]。与类标记信息相比,成对约束获取代价小,更容易获得[4],成对约束可由类标记产生;反之,则不行。因此,研究成对约束下的半监督特征选择算法具有一定的实用价值。
本文基于 RSC(relevant set correlation)模型[5],提出一种基于成对约束扩展的半监督网络流量特征选择PCFRSC(pairwise constraints feature selection based on RSC model)算法,通过寻找成对约束样本点的最相关邻居节点,并将其扩展到大量未标记的样本点上,通过少量的成对约束和大量的无标记样本有效地进行流量特征选择,解决网络流量分类中监督信息有限的问题。
1 相关理论
到目前为止,成对约束下的特征选择的方法研究比较少见,最具代表性的是张道强教授等人提出的基于成对约束的特征选择算法Constraint Score[6],首次尝试使用成对约束作为监督信息进行特征选择,但他只使用了少量的监督信息而忽略了大量无标记数据可能隐藏的重要信息。文献[7]提出的特征选择算法能同时利用正约束和负约束信息,但没有利用在未标记样本中隐藏的潜在信息来实现半监督特征选择。Zhang D Q等人提出一种半监督维数约减(SSDR)算法[8],该算法能同时保持成对约束的结构和未标记数据在低维流形的结构,其缺点是没有考虑低维流形的局部结构。文献[9]提出将类标号从少量的训练样本集扩展到大量的未标记样本的框架,实验证明其有一定的有效性,但仍未能充分利用大量未标记样本。王博[10]针对半监督信息缺乏的情况,提出一种半监督的特征选择算法SFRSC,对少量的已标记样本进行了扩展,但其假设初始的已标记样本集中包含了所有的类别信息,也没有考虑容易获得的样本间的成对约束关系。
2 基于成对约束扩展的半监督网络流量特征选择算法
2.1 RSC 模型
学者Houle M E首次提出RSC模型,随后将RSC模型运用于无监督特征选择,提出了RSCF算法[11]。本文的研究与之类似,但不同的是:RSCF算法仅利用了未标记样本的无监督算法,而本文的算法是同时利用了成对约束和未标记样本的半监督学习方法。
样本集间的相关度和样本集的自相关度的定义如下:
定义1 设A,B⊆S,|S|表示结合中元素的个数,则集合A与B的相关度可表示为

定义2 集合A在全集S上的自相关度定义为
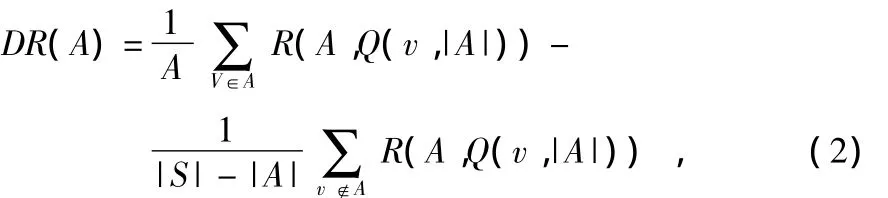
式中Q(v,|A|表示由v的|A|个近邻组成的样本序列,A的相关度由集合A中所有元素决定,对任意v∈A,如果v与所有的v∈A/v都是强相关的,而v与所有的v'∈S/A都是弱相关的,则S中与v相似度高的样本都属于A。
2.2 扩展成对约束
原始的成对约束集称为初始约束集,它包括正约束(must-link,ML)和负约束(cannot-link,CL)。ML表示 2 个样本属于同一类,CL表示2个样本不属于同一类。为达到扩充训练集的目的,需从初始成对约束集扩展出新的成对约束ML'和CL',这些新扩展的样本又可以作为核心点继续向四周扩展。成对约束虽然包括正约束和负约束,由于在实际计算过程中,正约束只能扩展出正约束,负约束却可以同时扩展出正约束和负约束,因此,为提高算法性能,算法只使原始约束集中的负约束进行扩展。
对任意一个负约束(x,y)∈CL,首先利用式(3)得到K1,那么在训练集S中,包含x的具有最大的内相关性样本集就是A=Q(x,k1),这表明A中的样本相关性强,因此,它们应该属于同一类

同理,可求得y的同类样本集合B。利用集合A和B,可得到新的正约束集合ML'和新的负约束集合CL'分别是

以图1~图3为例来形象地说明约束扩展的过程。如图1所示,空心圆表示未知类型样本,实心的形状表示成对约束,不同形状的实心形状表示不同的类别,相同形状的实心圆表示同种类别。图1表示的是初始情况,表示有4种不同的类别样本。以图1为核心,根据式(3)得各自的集合A。在A中,未标记的样本点和实心的样本所属的类别相同,经过第一步的扩展得到图2。图3又把图2作为起始点重复第一步的过程进行扩展。直到所有的样本点都被预测,扩展才结束。但该扩展中存在一个问题,在最后的划分结果中可能出现约束违反问题(即划分重叠),如图3中的点P同时属于实心圆和实心五边形两类,原因在于用于划分的式(3)得到的是局部最优。图3中的P点同时属于多类别的划分是应该避免的,将在3.3节中给出详细的解决方案。

图1 约束扩展过程(1)Fig 1 Constraints extension process(1)

图2 约束扩展过程(2)Fig 2 Constraints extension process(2)

图3 约束扩展过程(3)Fig 3 Constraints extension process(3)
2.3 消除违法约束
由图1~图3可知,在把负约束(x,y)∈CL扩展出集合A和B的过程中,可能存在样本v∈A∩B,由它扩展出新成对约束(x,v)∈ML',(y,v)∈ML',,由传递性可知(x,y)∈ML',即x,y属于正约束对,这与(x,y)∈CL相矛盾,此时便产生了成对约束违反问题。解决这个问题的方法就是将v划分给一个集合A或者B,划分依据是通过分别计算v对集合A或者B的自相关度贡献来判断其归属,贡献大小由式(4)中的IR1评估,值越大表示贡献越大

计算IR1(v|A)和IR2(v|B),若IR1(v|A)>IR2(v|B),表明v对集合A的贡献越大,因此,把v划分给集合A;反之,则把v划分给集合B。如果IR1(v|A)=IR2(v|B),则随机选择类型。
注意到,式(4)中,只考虑了样本v对单个集合自相关度的贡献,而未考虑划分v后对集合A,B产生的影响。式(5)基于这样的思想:同时考虑v对单个集合的自相关度的影响和v划分后对2个集合的相关度的影响。把v划分给A,当且仅当v对A的自相关度高,且把v划给A后的集合与集合B的相关度弱。通过利用式(5)计算比较IR2(v|A,B)和IR2(v|B,A),当IR2(v|A,B)>IR2(v|B,A)时,把v划分给A;否则,把v划分给B

2.4 PCFRSC 算法描述
Input:training data setX={xi},Must-link setML,Cannot-link setCL
Output:Extended set of constraintsML'andCL'
1)InitializingML'=ML,CL'=CL
2)foreach Cannot-link(x,y)inCL
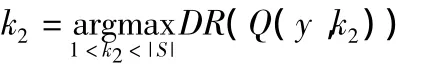
b.A=Q(x,k1),B=Q(y,k2)
c.If there isv∈A∩B,dividevto eliminate the constraint violation by the formula(5),if there is no,jump to 2.4
d.Extending pairwise constraints.

3)returnMLandCL'.
3 实验结果与分析
3.1 实验数据
实验采用剑桥大学计算机系Moore A W教授等人在文献[12]中所用的实验数据集,本文简称Moore-set。Mooreset共有377526条数据,是目前最权威的网络流量数据集,它包含10个数据子集,每一个数据子集均包含数万条数据。每条流包含249项属性,由端口号等网络属性和平均间隔时间等统计属性组成。最后一项属性为分类目标属性,表明该样本的流量类型,如WWW,FTP,P2P等。
实验过程中,选用已有的成对约束特征选择算法Constraints-Score1(Cs1)和 Constraints-Score2(Cs2)[6],且设定Cs2的参数=0.1,与本文提出的PCFRSC算法相比较。分类器使用Weka软件中的3-nearest-neighbor分类器(3nn)。实验所用的数据处理和分析工具是Matlab 7.1和Weka 3.7。Moore-set总体流量数据统计信息如表1所示。

表1 Moore-setTab 1 Moore-set
3.2 在分层抽样子集上的分类效果
从10个Moore-set数据子集中随机抽出2个子集,分别称作set-u和set-t,这2个样本中每类样本的比例与Mooreset保持一致,从set-u中抽取每类应用的1%的样本作为训练集,用PCFRSC,Cs1和Cs2在此训练集上训练获得相应的网络流量分类器,并用测试数据集set-t对训练出的分类器进行验证。实验重复10次,对结果取平均值,比较Cs1、Cs2和PCFRSC在不同原始成对约束下的分类精度,实验结果如图4所示。

图4 分层抽样下的分类性能Fig 4 Classified property in stratified sampling
从图4可以看出:在分层抽样的条件下,PCFRSC算法的分类精度明显高于Cs1和Cs2,但在成对约束较少的情况下,PCFRSC相对于Cs1和Cs2没有明显的优势,而当成对约束的数量超过15,PCFRSC算法分类精确的提高非常明显,虽然Cs1和Cs2的精度也呈现增长的趋势,而是提高比较缓慢。说明PCFRSC能在成对约束有限的情况下,扩展成对约束,较充分地利用成对约束和无标记样本来进行特征选。但当成对约束的数量比较多时,PCFRSC和Cs1,Cs2的分类精度反而有所下降,这说明当成对约束的数量较多时算法并不敏感,过多的先验知识不能过快地提高分类精度。
3.3 在均匀抽样子集上的分类效果
分别抽取Moore-set每个应用类型的1 000个样本(由于INTERACTIVE和GAMES的数量较少,不具代表性,因此,在本实验中不采用这2种数据),形成一个新的各类样本数量相等的训练集set-u1,从10个Moore-set中随机选择一个子集作为测试集set-t1。用PCFRSC,Cs1和Cs2在此训练集上训练获得相应的网络流量分类器,并用测试数据集set-t1对训练出的分类器进行验证。实验重复10次,对结果取平均值。比较比较Cs1,Cs2和PCFRSC在不同成对约束下的分类精度,实验结果如图5所示:

图5 均匀抽样下的分类性能Fig 5 Classified property in uniform sampling
从图5可以看出:在分层抽样的条件下,PCFRSC算法的分类精度也明显高于Cs1和Cs2,PCFRSC整体上还保持了较高的分类精度和较好稳定性,分类精度平均提高了4%左右,在原始成对约束在20~25之间的时候,表现出了最佳的分类性能。但PCFRSC的性能也不是随着成对约束的增多而不断提高,当约束的数量较多时,PCFRSC的分类性能反而下降,因为成对约束越多,由约束扩展产生噪音样本的可能性就越大,计算的复杂度也越高。但总体而言,新的成对约束扩展方法PCFRSC是有效和可行的。
当训练集的样本构成比例不一样时,对特征选择和分类效果也会产生不同的影响。分层抽样的方法更利于大样本,均匀抽样的方法更利于小样本。从图4和图5可知,约束扩展能较好地弥补成对约束数量上的不足,扩展的成对约束在一定程度上反应了数据的分布信息,两者相互促进。在监督信息较少的情况下,半监督特征选择方法能同时利用少量有限监督信息和大量无监督信息,保证了成对约束扩展的健壮性。
4 结束语
本文基于RSC模型提出了一种半监督网络流量特征选择算法PCFRSC,该算法以原始成对约束为核心,将其扩展到未标记样本上,同时进一步解决了成对约束违反问题。与未进行成对约束扩展的算法相比,PCFRSC算法是比较有效的。但PCFRSC还存在一些需进一步改进的地方,比如建模的时间较长,分类的精度还有再提升空间。
[1] 张 宾,杨家海,吴建平.Internet流量模型分析与评述[J].软件学报,2011,22(1):115 -131.
[2] 刘 琼,刘 珍,黄 敏.基于机器学习的 IP流量分类研究[J].计算机科学,2010(37):35-39.
[3] Ming Yang,Jing Song.A novel hypothesis-margin based approach for feature selection side pairwise constraints[J].Neurocomputing,2010,73:2859 -2872.
[4] 韦 佳,彭 宏.基于局部与全局保持的维数约减方法[J].软件学报,2008,11(19):2833 -2842.
[5] Houle M E.The relevant-set correlation model for data clustering[J].Statistical Analysis and Data Mining,2008(1):157 -176.
[6] Zhang D,Chen S,Zhou Z.Constraint score:A new filter method for feature selection with pairwise constraints[J].Pattern Recognition,2008,41(5):1440 -1451.
[7] Yeung D Y,Chang H.Extending the relevant component analysis algorithm for metric learning using both positive and negative equivalence constraints[J].Pattern Recognition,2006,39(5):1007-1010.
[8] Zhang D Q,Zhou Z H,Chen S C.Semi-supervised dimensionality reduction[C]∥Proc of the 7th SIAM Int'l Conf on Data Mining,2007:629-634.
[9] Ren Jiangtao,Qiu Zhenyuan,Fan Wei,et al.Forward semi-supervised feature selection[C]∥PAKDD,2008:970 -976.
[10]王 博,贾 焰,田 李.基于类标号扩展的半监督特征选择算法[J].计算机科学,2009(36):189-191.
[11] Houle M E,Nizar Grira.A correlation-based model for unsupervised feature selection[C]∥CIKM,2007:897 -900.
[12] Moore A W,Zuev D.Internet traffic classification using Bayesian analysis techniques[C]∥Proc of 2005 ACM SIGMETRICS Int'l Conf on Measurement and Modeling of Computer Systems,2005:50-60.

