基于无速度传感器观测器的转速辨识
郭凤仪,王 洋,丁永峰
(辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105)
0 引言
矢量控制技术得以有效应用的前提在于电机磁链和转速度信息的准确获取。近年来,出现了大量的速度估计方法,而无速度传感器控制系统的核心问题便是对转子的速度进行有效估计,出发点就是用直接计算、参数辨识、状态估计、间接测量等手段,测量定子侧的电量,如定子电压和数学模型的计算。本文将通过算法分析对传统速度观测器进行改善设计,以扩展Luenberger观测器为基础,对速度观测器的增益矩阵选择方法进行深入研究,提出了一种简化的增益矩阵选择方法,利用优化算法分析,结合模型参考自适应系统(MRAS)结构实现了转子速度估计精度的提高[1~3],并有效改善了观测器系统的稳定性能。
1 系统原理与增益计算
1.1 系统实现原理
通过对观测器的选择、增益算法分析、结合转矩观测进行速度的辨识,以及MRAS算法实现对转子速度的有效的动态估计设计。
全面考虑,本转速估计设计的速度观测器选择采用扩展 Luenberger观测器(ELO)[4,5],速度估计原理如图 1 所示。因适用于非线性时变系统,从而在高性能转矩控制异步电机调速系统中,所得到的估计偏差较小。此外,可以用常规的控制系统设计方法(调整极点位置)来调节ELO的暂态行为,而且这种调节不会使静态性能变坏。所以,在转矩控制异步电机的调速系统中,对转子磁链采用ELO不仅可以获得精确的速度估计,还能获得快速的暂态响应。虽然在低速时对转子速度和转子磁链的非线性估计性能会有所降低,但只要在接近零速系统不是匀速运行,不会构成严重问题。所以,在高性能无速度传感器调速系统中,采用合适的观测器是电机稳定运行的前提保证。

图1 扩展Luenberger观测器速度估计原理Fig 1 Speed estimation principle of extended Luenberger observer
由于观测器以定子电流矢量和转子磁链矢量为状态变量,异步电机在两相静止α-β坐标下的数学模型可得相应的观测器模型为

式中 “^”表示对应变量的估计值;G1=-(g1r+jg1i),G2=-(g2r+jg2i),均为增益系数。
1.2 观测器增益计算
增益选择是观测器应用中的一个难点,它直接影响着观测器的收敛速度和稳定性。根据Lyapunov稳定性理论,状态观测器渐近稳定的条件是存在一个对称的正定矩阵P使得下面的不等式(3)成立

假设ω是允许的转速上界,当转速在区间[-ω,ω]变化时,误差方程式的鲁棒稳定条件可以由式(4)和式(5)两个不等式来确定
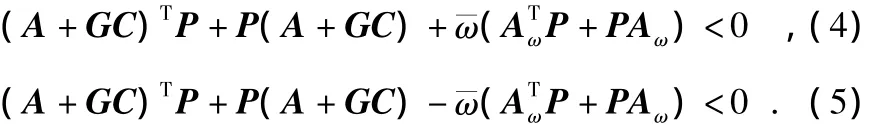
不等式(4)和式(5)是关于矩阵变量P和G的双线。
在整个观测器应用系统中增益的选择是个关键问题,它直接影响着观测器的收敛速度和稳定性能。传统解决方法是让观测器极点POb正比于电机极点PIM,即POb=kPIM,k≥1,为比例系数。这种方法因为在放大极点实部的同时也放大了虚部,所以,在高速时可能会造成不稳定。满足POb=kPIM条件的增益矩阵中[6],其中,比较简单的一组解为

为了保持观测器极点的虚部不变,将实部在复平面上向左平移,即POb=PIM+b(b<0),在静止坐标系下推导可得增益的表达式

在无速度传感器应用中,增益中所含有转速ωr要换成估计的转子转速^ωr,因此,会受到估计转速精度的影响,由于是时变的,在计算中要实时更新,增加了实现的难度。为了简化计算,本文提出一种简化算法,即令ωr→∞ ,相应的增益矩阵变为常数如式(8)所示,从而简化了计算,有利于实时实现

2 参数辨识方法分析
本文结合转矩观测对速度相关参数的辨识方法进行详细分析,首先利用Lyapunov定律[7]推导可得到转子转速和定子电阻的自适应律

式中 Δi=i-^i为测量电流和观测电流之差;k1和k2为正常数。实际中为了提高动态响应速度,采用 PI来代替式(9)和式(10)中的纯积分。引入转矩观测的速度辨识可以用式(11)和式(12)来表示

式(11)和式(9)相比,引入了电机运动方程,可以加快转速估计的动态响应。
转速观测环节采用了基于超稳定理论推导的自适应结构速度估计方式如图2所示,即模型参考自适应系统(MRAS),是利用2个不同的输入变量、2个不同结构的电机模型来估计电机的同一变量。其中,不涉及被估计量的电机模型被称为参考模型,涉及到被估计量的电机模型被称为自适应模型。利用这2个模型输出量的误差来驱动1个自适应机制,自适应机制产生1个转速的估计值;再利用转速估计值来修正自适应模型,当自适应模型的输出和参考模型的输出完全相等时,理论上自适应机制的输出就等于电机实际转速;否则,自适应机制将不断调节,直到满足误差要求。参考模型和自适应模型的输出可以选择转子磁通空间矢量、反电动势、无功功率等。

图2 模型参考自适应系统原理Fig 2 Principle of model reference adaptive system
MRAS的特点如下:1)是基于稳定性理论设计的参数辩识方法,这保证了参数估计的渐进收敛性;2)是一种自适应控制方法,对电机参数变化和外界扰动具有较强的鲁棒性;3)速度估计是以参考模型为基础的,所以,参考模型本身的参数准确程度直接影响到速度辩识的准确程度。
MRAS可以采用不同的状态变量作为速度整目前,大量的MRAS都是基于超稳定理论推导的自适应结构(通常可以为PI)进行速度估计。这些方法的自适应模型都是确定的数学模型,便于数字实现。然而数学模型的使用不同程度地影响了速度估计的精度和鲁棒性。因此,采用基于人工智能(神经网络、模糊控制等)的非线性自适应模型成为了目前模型参考自适应方法发展的方向。
3 仿真结果
为了进一步验证上述观测方法可行性,本文在Matlab/Simulink下构建了仿真模型[9,10],电动机选用三相鼠笼型异步电动机,其额定容量为2200 VA;额定电压为220 V;额定频率为 50 Hz。定子相应参数RS=0.877,LS=4.34 mH,转子相应数Rr=1.47,Lr=4.34mH,互感Lm=160.8mH,所带负载选用阶跃函数,仿真时间取T=3 s。在空载的前提下,对调速控制系统的给定速度指令为1000~100 rpm,再回到1000 rpm,此时,系统响应波形观测值如图3和图4所示;带负载的前提下对调速控制系统速度的给定指令为500~800 rpm,再回到500 rpm,其响应波形观测值如图5和图6所示。
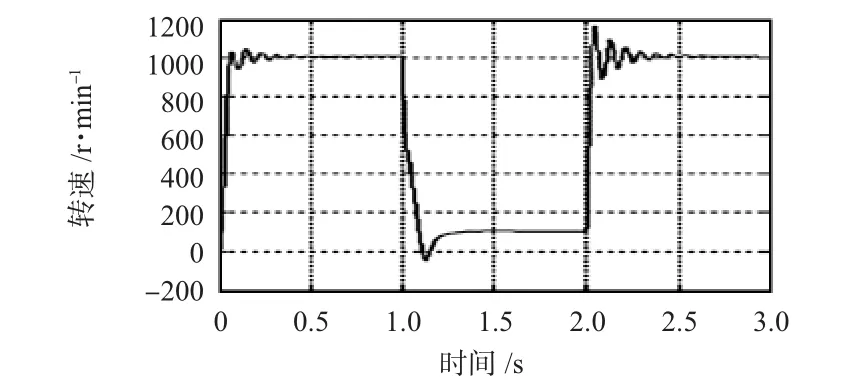
图3 空载时转速观测结果Fig 3 Observed result of rotational speed under no-load
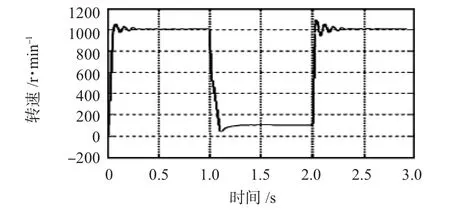
图4 空载时转速实际变化Fig 4 Actual change of rotational speed under no-load

图5 带负载时转速观测结果Fig 5 Observed result of rotational speed under load
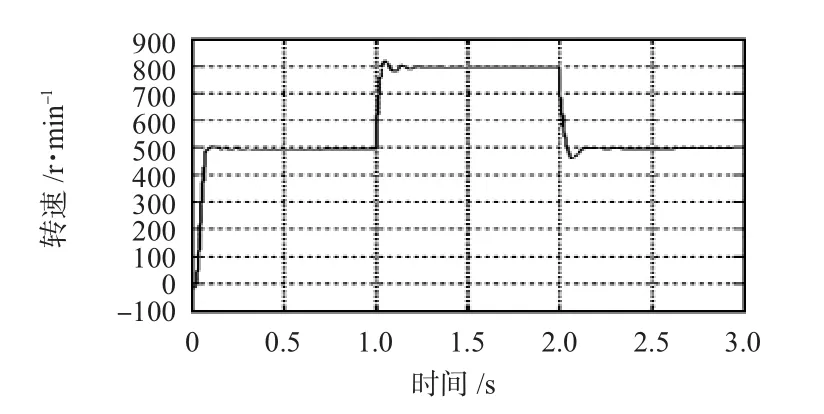
图6 带负载时实际转速变化Fig 6 Actual change of rotational speed under load
通过两次改变速度给定值,观测响应速度的测定结果。图3、图4中空载时采用此速度观测方法几乎接近电机的实际稳定转速度给定值1000 rpm或100 rpm,超调波动很小,精确度与稳定性可以满足实际需要。由图5和图6可以看出:带负载前提下该观测方法同样有明显不错效果,观测值同样非常接近电动机的实际稳定速度给定值500,800 rpm,且基本没有超调波动,速度估计相应快且精度高,性能达到了期望水平。
4 结论
本文通过介绍和研究一种新型的速度观测系统,对其进行了原理介绍以及具体观测环节进行相应算法分析,并构建了相应仿真模块。通过仿真实验结果表明:该方法能及时准确的辨识转速,解决了传统速度观测方法的反应慢、精度低、稳定性差等问题,在大范围速度情况下都能稳定工作,对未来开发和研究调速系统相关方向具有一定意义。
[1] 金 海,黄 进.基于模型参考方法的感应电机磁链的自适应观测及参数辨识[J].电工技术学报,2006,21(l):65 -69.
[2] Hinkkanen M.Analysis and design of full-order flux observers for sensorless induction motors[J].IEEE Trans on Industry Applications,2004,51(5):1033 -1040.
[3] 陈 硕,Tsuji M.基于磁通观测器的感应电机无速度传感器矢量控制系统[J].电工技术学报,2001,16(4):30 -33.
[4] 韦立群,刘丛伟.一种消除电压型磁链观测器中直流偏置误差的新方法[J].清华大学学报:自然科学版,2001(9):51-54.
[5] Vas P.Sensorless vector and direct torque control[M].Oxford:Oxford University Press,1998:34 -40.
[6] Boyd S,Feron E.Linear matrix inequalities in system and control theory[M].Philadelphia:SIAM,1994.
[7] Kubota H,Matsuse K.DSP-based adaptive flux observer of induction motor[J].IEEE Trans on Industry Applications,1993,29(2):344-348.
[8] 毛晓英,罗文广.基于Matlab/Simulink的异步电动机矢量控制调速系统仿真[J].东北电力技术,2004(1):14-16.
[9] 薛定宇,陈阳泉.基于Matlab/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002:192-202.

