小型风力机叶片的流场仿真和应变实验研究

侯 西，张锦光，胡业发

（武汉理工大学机电工程学院，湖北 武汉 430070）

风能作为清洁的可再生能源，其开发潜力已被世界各国所认可。叶片是风力机组捕获风能的关键部件，在实际运行环境中承受离心力、流体动力振动、温差（热应力）、介质等的综合作用［1－2］，裂纹在恶劣的环境下频繁地产生，对风力机组安全运行构成很大威胁，也给企业带来极大的经济损失。因此，对风力机叶片应变进行实时监测是完全必要的。

作为新型的传感器，光纤光栅结构简单，尺寸小，精度高，可以组成传感网络进行分布式测量，且具有灵敏度高、绝缘、抗电磁干扰、耐高电压、耐化学腐蚀和耐高温等优点，满足叶片运行时复杂环境下的传感应用要求［3－4］。由于光纤光栅直接测量的物理量是温度和应变，因此笔者分析了空气载荷下叶片的应变分布，将有限元计算和光纤光栅实验测量的应变值进行了对比。

1 叶片CFD流场仿真分析

1.1 叶片的几何建模

利用三坐标测量仪对叶片进行扫描，然后导入3D绘图软件Pro/E进行建模，完成的模型如图1所示［5］。将叶片以风轮轴为中心阵列，设置数量为3个，角度为120°，便完成了3个叶片实体的建模。

图1 Pro/E中叶片的模型

1.2 叶片网格划分和边界条件

将叶片模型在Pro/E环境中保存为.step格式的文件，导入到GAMBIT前处理器中，再进行网格划分。叶片的直径d=1.2 m，设置流体的圆柱体计算区域直径为2 m，长度为12 m，左边为速度入口，到风轮圆盘的距离为4 m，右边为压力出口，到风轮圆盘的距离为8 m。叶片的网格划分为四面体，流场的网格划分为六面体，如图2所示。

图2 风力机计算域网格图

1.3 仿真结果分析

图3 叶片迎风面静压分布云图

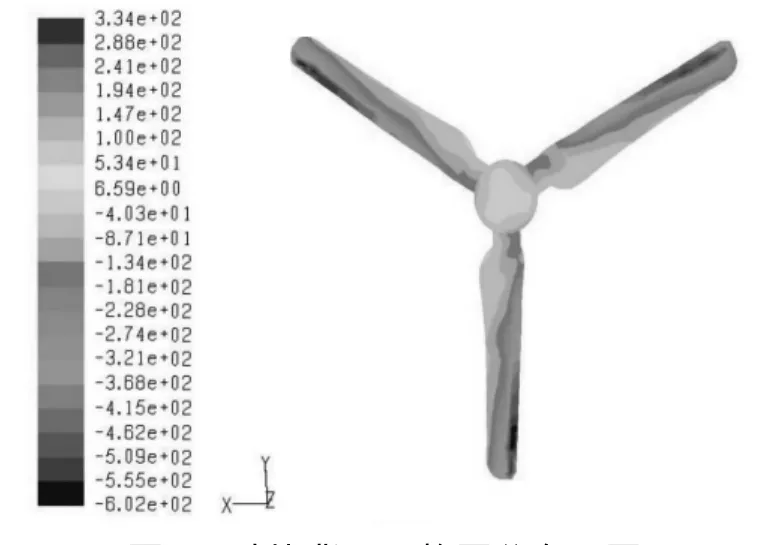
图4 叶片背风面静压分布云图

图3和图4分别为叶片迎风面和背风面的静压分布云图，当叶片在12 m/s风速的风场环境中以额定转速400 r/min旋转时，叶片迎风面的压强为正，背风面压强为负，气流压强不平均地分布在表面。在叶片的迎风面，叶尖靠近前缘的区域压强值最高，变化范围为288～334 Pa，叶片中间和根部压强较低，变化范围为100～241 Pa；在叶片的背风面，叶尖靠近前缘的区域压强值最低，变化范围为－602～－228 Pa，叶片中间和根部压强较高，变化范围为－181～－31.4 Pa。旋转时叶片上下表面的最大压力差为936 Pa，位于叶尖。当半径减小时，叶片的线速度减小，与气流的相对速度减小，压力差也随之减小。当叶片在额定工况下运行时，叶片表面的静压主要分布在0.2倍半径到叶片尖端，此段区域的叶片吸收风能转化为动能。

2 叶片空气载荷计算

作用在风轮上的风力是风力机的主要动力源，也是叶片所承受载荷的主要来源，根据流体仿真的结果可知，叶片表面的静压主要分布在0.2倍半径到叶尖，即叶片的气动载荷主要分布在该区域。

［6］，根据葛劳渥旋涡理论和叶素动量定理，叶片长度方向上的升力元和阻力元为:

升力和阻力可分解为作用在叶片上沿风向的推力和沿叶片旋转方向的周力，分别为:

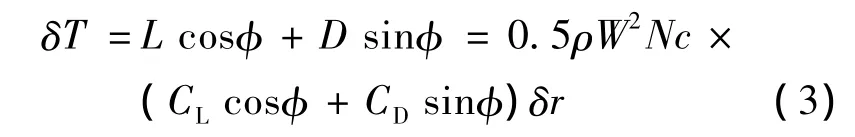
其中:W为叶片线速度与来流风的相对合速度；N为叶片数；r为叶尖半径；c为弦长；φ为叶片相对合速度与旋转面之间的夹角；CL为翼型的升力系数；CD为翼型的阻力系数，可由翼型的气动力特性曲线查出。

选取叶片的叶尖速比λ=6，参考式（1）～式（4），计算叶片不同半径位置处（0.3r、0.5r、0.7r、0.9r）的推力和周力，各段叶素长度为0.2r，折算成加载在叶尖的等效推力和周力如表1所示。随着风速的增大，叶片的推力和周力近似线性增大。由于推力是叶片产生应变的主要载荷形式，因此选取推力为叶片的载荷加载在叶尖［7－8］。

表1 不同风速下加载在叶尖的等效推力和周力

3 叶片应变实验方案

采用分布式测量的方法，在叶片上表面的左侧边缘、中间、右侧边缘的表面分别粘贴3根光纤，每根光纤上串接有5个不同中心反射波长的光栅，中心反射波长分别为1290 nm、1293 nm、1303 nm、1305 nm、1308 nm，每个光栅间隔 0.2倍叶片半径的距离，叶片以悬臂梁的形式，叶根固定，叶尖加载等效推力［9］，静载荷光纤光栅应变实验简图如图5所示。

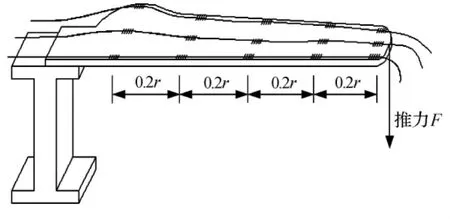
图5 静载荷光纤光栅应变实验简图

4 ANSYS计算与实验数据对比分析

将叶片的模型导入ANSYS软件，选择solid45单元进行应变分析，图6为叶尖加载推力为31.6 N时叶片表面应变分布云图，并将有限元计算与实验测量数据进行对比。

4.1 31.6 N推力下叶片表面各点的应变分布

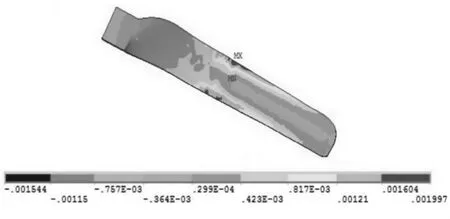
图6 叶片表面应变分布云图

表2和表3分别为叶尖推力为31.6 N时叶片左侧、右侧各点实验测量和有限元计算的应变值。对比可知，在叶片0.6倍半径处的应变值最大，叶尖和叶根的应变值最小，这是由于小型风力机叶片根部（0.2倍半径处）的弦长最长，刚度最大，载荷施加在叶尖时，沿叶片翼展方向刚度较小的中间段部位最容易弯曲变形［10］。

表2 叶片左侧点应变值

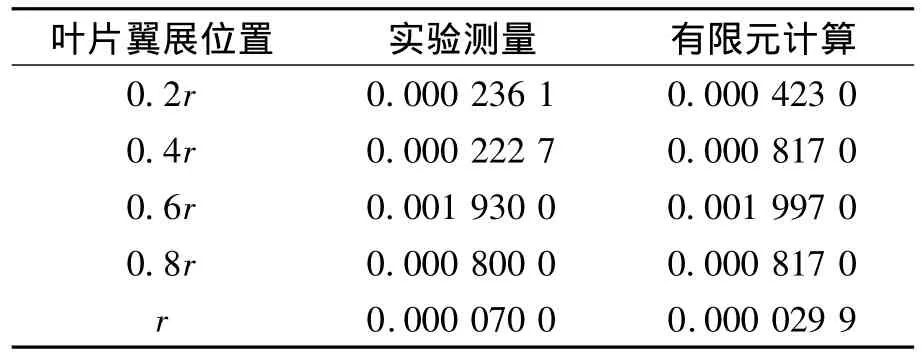
表3 叶片右侧点应变值

比较实验测量和有限元计算的应变值，在应变最大的叶片0.6倍半径处，左侧的误差为－2.1%，右侧的误差为3.3%，实验测量和理论计算基本吻合。在叶片的最大应变部位，实验测量值和有限元计算值的误差较小，在应变较小的部位，由于实验测量和理论计算的误差，导致偏差较大［11］，但是，两者的结果趋势一致，如图 7和图8所示。

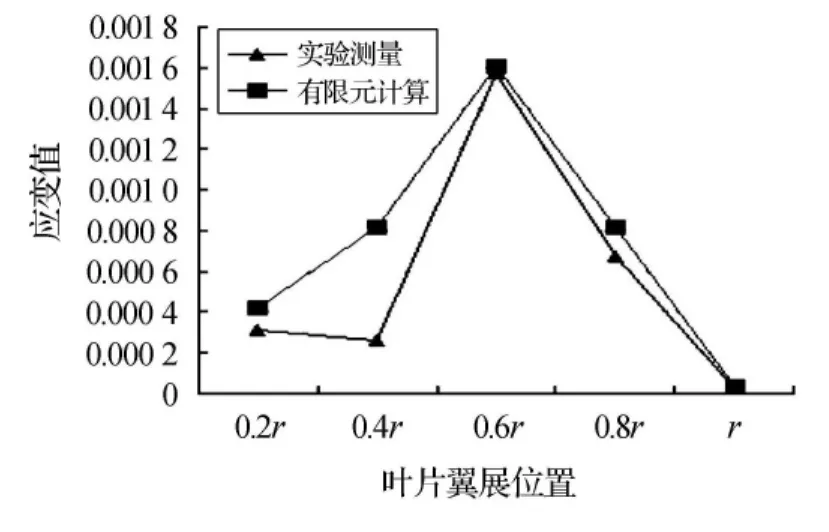
图7 叶片左侧点应变值

图8 叶片右侧点应变值

4.2 不同推力下叶片最大应变的变化趋势

表4和表5为不同推力载荷下（风速为7～12 m/s）叶片0.6倍半径处两侧各点的实验测量和有限元计算的应变值，其对应的曲线如图9和图10所示。对比可知，随着载荷的增加，叶片的应变值近似线性增加，实验测量和有限元计算的误差也逐渐减小。

表4 不同推力下叶片0.6倍半径处左侧点的应变值

表5 不同推力下叶片0.6倍半径处右侧点的应变值

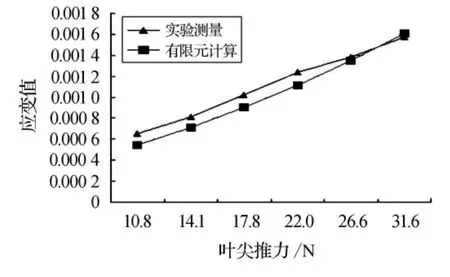
图9 不同推力下叶片0.6倍半径处左侧点的应变值

5 结论

从实验和理论计算结果可以得出以下结论:

图10 不同推力下叶片0.6倍半径处右侧点的应变值

（1）叶片0.6倍半径处应变最大；由于叶根的刚度最大，叶根附近的应变较小；叶尖处的应变最小。

（2）随着载荷近似线性地增加，叶片的最大应变值也近似线性地增加。

（3）在叶片的最大应变区，光纤光栅实验测量和有限元理论计算结果基本吻合。

参考文献:

［1］张晓明.风力发电复合材料叶片的现状与未来［J］.纤维复合材料，2006（2）:60－63.

［2］韩学群.大型风机叶片的设计改进［C］//第17届玻璃钢/复合材料学术年会论文集.北京:［s.n.］，2008:268－270.

［3］刘汉平，王建刚，赵圣之.光纤布拉格光栅的耦合模理论分析［J］.山东理工大学学报:理学版，2006，41（4）:89－92.

［4］刘微，李靖.分布式光纤光栅在管道检测中的应用［J］.红外，2008，29（7）:37 －39.

［5］钱杰，张锦光，吴俊.小型低风速风力发电机叶片设计［J］.武汉理工大学学报:信息与管理工程版，2010，32（5）:729 －732.

［6］陈圆.风力发电机叶片三维建模及有限元动力学分析［D］.西安:西安理工大学图书馆，2008.

［7］尹耀安.大型风力机叶片设计与CFD分析［D］.武汉:华中科技大学图书馆，2008.

［8］于勇，张俊明，姜连田.Fluent入门与进阶教程［M］.北京:北京理工大学出版社，2008:65－66.

［9］张春友，赵华洋，于立波.小型风力发电机叶片静载实验研究［J］.内蒙古民族大学学报:自然科学版，2009，24（3）:308 －310.

［10］TSALAVOUTAS A，MATHIOUDAKIS K，STAMATIS A，et al.Identifying faults in the variable geometry system of a gas turbine compressor［J］.Journal of Turbo Machinery，2006，128（4）:786 －797.

［11］SCOTT J S，MICHAEL C R.Horizontal axis wind turbine blade aerodynamicsin experiments and modeling［J］.IEEE Transactions on Energy Conversion，2007，22（1）:61 －70.