整体壁板参数化设计与敏感性分析
王 雯,王生楠,苏 毅
(西北工业大学 航空学院,西安 710072)
20世纪40年代以来,飞机机身主要是应用典型的蒙皮-桁条铆接结构.传统过程与结构细节制作过程结合在一起,已经非常的精确和成熟,如果在传统设计上没有实质性的改变,要想降低设计和制造成本是非常困难的.一种合适的替代方法是使用由蒙皮、桁条和框组成的整体结构.与传统组合结构相比,整体结构减少了结构重量,降低了生产成本,这源于部件数量的减少,同时使结构的抗腐蚀性大大增加.然而,与传统的组合结构相比,整体结构在损伤容限与破损安全方面还有待改进[1-2].
目前,整体壁板在航空领域得到了广泛的应用.许多研究都集中在定义一个可靠的方法来预测这种结构的损伤容限[3].筋条使裂纹分支,减缓了裂纹扩展速率.尽管铆接筋条可以得到很好的止裂效果,但是铆钉孔的应力集中会导致初始裂纹的萌生.此外,整体壁板可以提高视觉检查能力,从而增加检测出裂纹的可能性.因此,对含裂纹整体壁板的力学行为进行研究,以确定结构是否具有破损安全或安全裂纹扩展的能力具有重要的工程意义.在线弹性范围内,应力强度因子是确定含裂纹结构的破损安全应力和裂纹扩展的重要参数.对含裂纹加筋板应力强度因子的研究已见于较多文献,Chen[4]对拉伸时中心开裂有限加筋板裂纹尖端的应力强度因子进行了计算;Tsamasphyros[5]也研究了含裂纹加筋板的应力强度因子;Isida[6]曾对含裂纹有限加筋板中结构尺寸及边界条件对应力强度因子的影响进行过研究;Fossati[7]应用两种裂纹前缘模型对三维裂纹的扩展特性进行了研究.
本文采用参数化分析计算整体壁板的蒙皮应力强度因子,并在有限元结果的基础上计算了结构的剩余强度,给出了不同结构尺寸下的上述结果,同时对参数的敏感性进行了分析,给出了具有工程指导意义的参考曲线.
1 整体壁板
整体壁板是一个典型的用整体结构代替组合结构的例子,如图1所示.结构剖面细节尺寸见图2.该结构有六根筋条,材料选用2024-T351,材料性能参数由表1 给出.

图1 整体壁板三维示意图
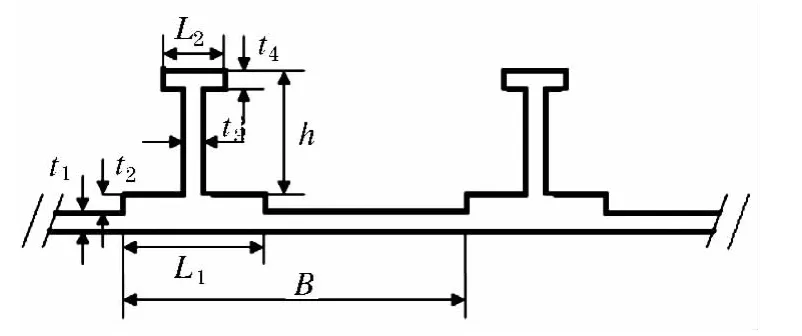
图2 剖面细节尺寸

表1 铝合金2024-T351 性能参数
2 参数化分析
进行有限元分析时,通常采用的是图形用户界面(GUI)操作方式的建模和分析方法,整个操作过程包括:建立几何模型、定义分析步和输出、定义相互作用、定义载荷与边界条件、划分网格、分析和后处理.如果要对某个或某几个几何参数进行修改时,就必须重新进行以上操作.在对不同几何参数的相同结构进行分析时,这个过程就会显得费时费力,极大地降低了工作效率,提高了设计成本.
本文使用Abaqus 脚本语言Python[8]对整体壁板进行参数化分析.Python 语言是一门功能强大的面向对象的编程语言,它允许在多种平台上编写脚本和快速开发.Abaqus 软件二次开发环境提供的脚本接口,就是基于Python 语言进行的定制开发.
Abaqus 脚本接口直接与内核进行通信,而与Abaqus/CAE 的图形用户界面(GUI)无关.编写脚本可以实现下列功能:
1)自动执行重复任务
2)进行参数分析
3)创建和修改模型
4)访问输出数据库(ODB 文件)
5)创建Abaqus 插件程序
Abaqus 脚本接口与Abaqus/CAE 的的通信关系如图3所示.
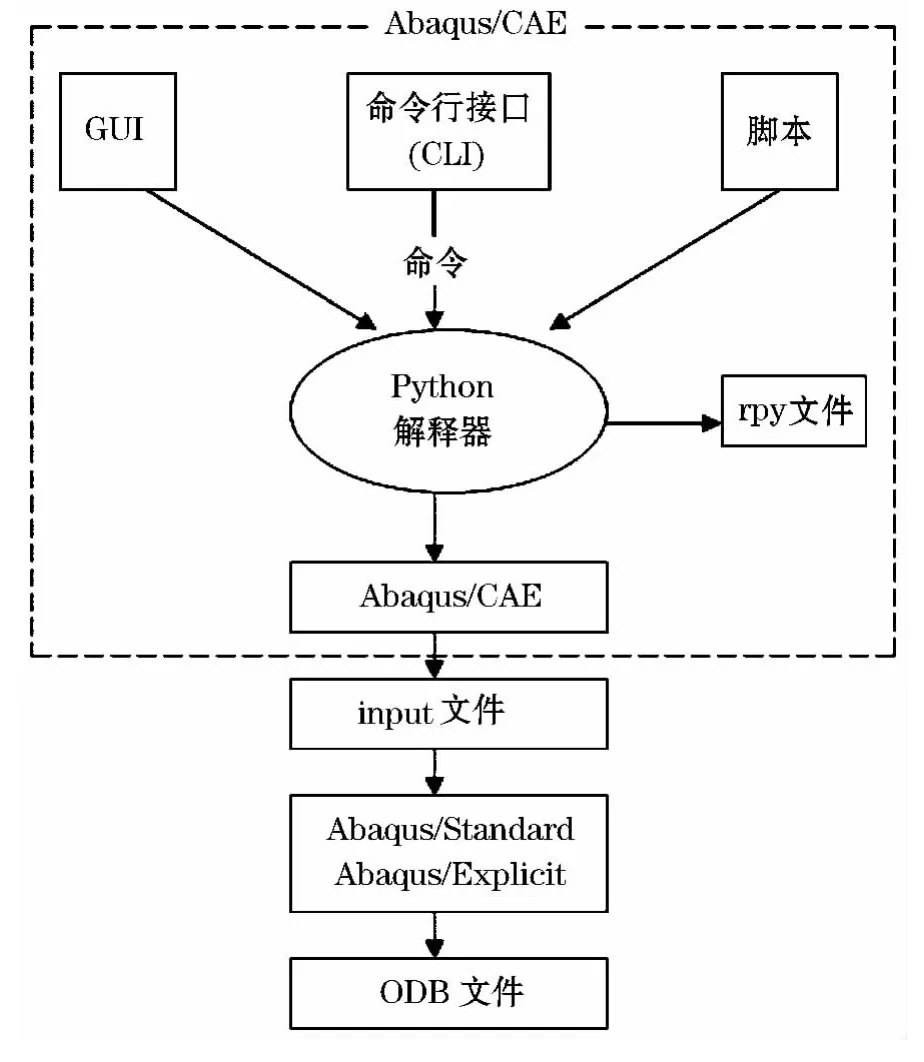
图3 Abaqus 脚本接口与Abaqus/CAE 的的通信关系
使用Python 语言对结构进行参数化分析使得整个分析过程具有理想的重复性、开放性和良好的修改性,参数化有限元技术对传统有限元分析所不具备的功能进行了充分的扩展,实现了按照用户的要求改变程序来满足特定的建模和分析需求,可以非常方便地得到相同结构不同几何尺寸的有限元模型和分析结果,提高了工作效率,降低了人工成本,对优化结构、降低成本和提高品质都有重要作用.
3 有限元模型
对整体壁板进行有限元模拟,该壁板带有六根筋条,在其中央位置人为假定有初始半裂纹长度为5 mm 的中心穿透裂纹,裂纹扩展方向垂直于筋条轴线;在蒙皮和筋条上施加平行于筋条轴线的均匀拉伸应力100 MPa.由于几何形状和边界条件的对称性,对整个结构的1/4 进行建模分析,并在对称面内施加对称边界条件.如图4所示,是半裂纹长度为29 mm 时的有限元模型.图5 给出了经过计算后的裂纹尖端应力云图,可以看到在裂纹尖端区域有明显的应力集中.
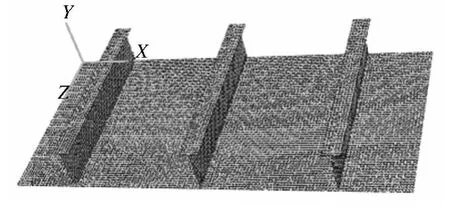
图4 有限元模型
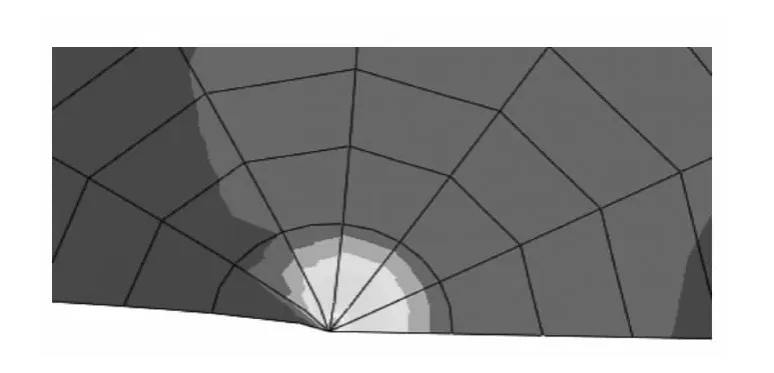
图5 裂纹尖端应力云图
4 断裂力学参数有限元计算结果分析
由于对结构施加的载荷为简单拉伸,在此只分析裂纹从中部蒙皮向两侧均匀扩展并跨过筋条的Ι 型应力强度因子.整体壁板结构参数为t1=4.0 mm、t2=2.0 mm、t3=6.0 mm、t4=6.0 mm、L1=24 mm、L2=22 mm、h=59 mm、B=172 mm.在裂纹穿过筋条后,假设筋条裂纹以与壁板裂纹扩展相同的速度向筋条上缘方向扩展,当然,这种假设是偏保守的,实际情况是筋条上裂纹扩展相对蒙皮裂纹扩展速度要更慢一些[9].蒙皮上的应力强度因子变化曲线如图6所示.
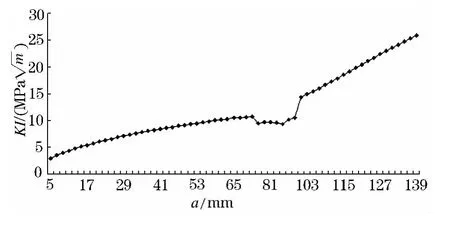
图6 蒙皮应力强度因子变化曲线
当裂纹距离筋条较远时,裂纹尖端的Ι 型应力强度因子基本呈线性增长;裂纹接近凸台时,应力强度因子出现了明显的减小,这是由于凸台的存在使得蒙皮厚度发生了突然的增大,结构刚度随之增大,所以裂纹张开受到了限制;裂纹在凸台上扩展时,应力强度因子增大的并不明显,但当裂纹接近筋条时,由于筋条的止裂作用,应力强度因子随着裂纹长度的增加而减小,当裂纹到达筋条时,应力强度因子减小到最低;裂纹继续扩展,穿过筋条后,原本由筋条承受的应力转移到蒙皮上,应力强度因子随之增大;当裂纹还在凸台上扩展时,由于厚度的增大,凸台上的裂纹应力强度因子并没有大幅度的增大,裂纹一旦离开凸台,蒙皮上的应力强度因子就出现了明显快速的增大.
计算综合修正因子β.由应力强度因子表达式
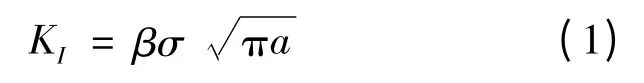
可以得到综合修正因子

其中:σ为参考应力,a为中心穿透裂纹半裂纹长度.
通过计算得到结构综合修正因子变化曲线如图7所示,β 集中反映了结构几何形状、裂纹几何形状和长度、加载方式以及相邻结构的裂纹引起的载荷再分配等因素.由图7 可知,由于加载方式为简单拉伸,裂纹主要是Ι 型裂纹,该曲线主要就是反映了结构几何形状和裂纹长度对应力强度因子
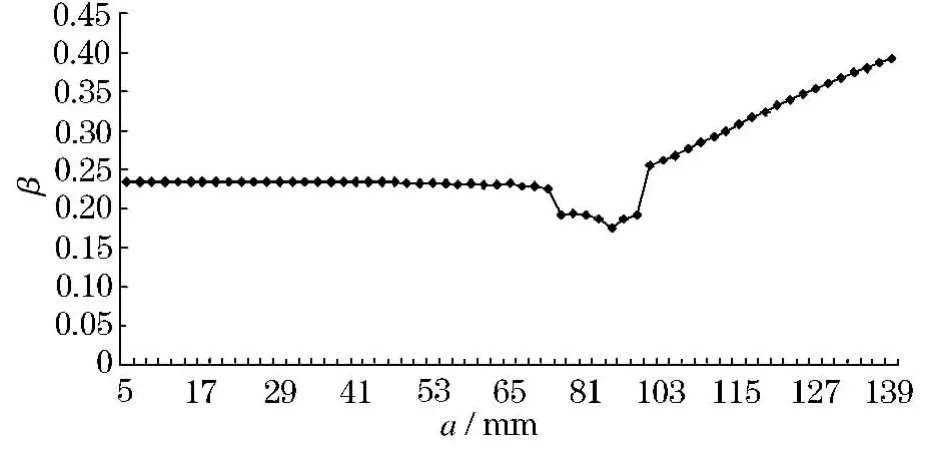
图7 综合修正因子变化曲线
的影响,所以在接近凸台和筋条处的曲线变化趋势与图6 基本一致,这里不再赘述.
结构剩余强度[σ]rs的计算.根据线弹性断裂力学理论,当应力强度因子K 达到临界值KC(断裂韧度)时断裂就会发生.由式(1)可求得结构的剩余强度为
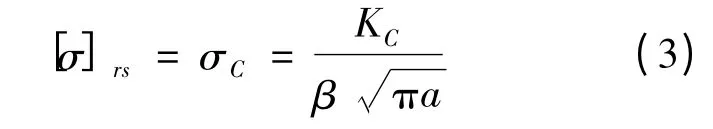
结合本文实际,代入临界应力强度因子KIC和图7 得到的综合修正因子β 有
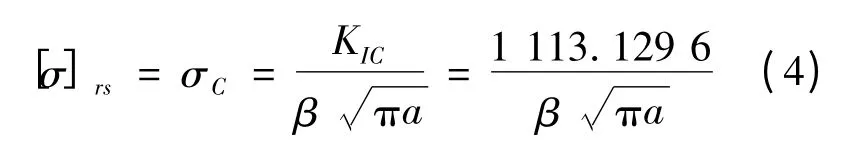
其中:
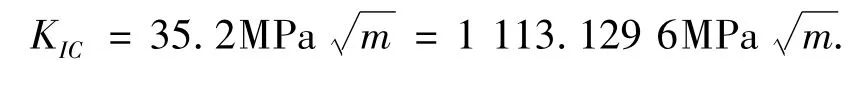
因此,得到结构的剩余强度曲线如图8所示.裂纹的存在极大地削弱了结构的剩余强度.随着裂纹长度的增加,整体壁板的剩余强度在裂纹较短时快速降低,而后降低速度有所减缓;凸台和筋条的存在使得结构的剩余强度明显增大,这说明凸台和筋条对整个结构的承载能力有积极的作用.
图8 剩余强度变化曲线
5 结构敏感度分析
为了分析不同结构参数对整体壁板损伤容限性能的影响,本文分别对该结构的3个主要几何参数进行了分析.
分别取t1=4.0、4.5、5.0、5.5、6.0、6.5 mm,其他参数保持不变进行有限元分析.得到t1变化时的蒙皮应力强度因子(图9)和剩余强度曲线(图10).
可见,当蒙皮的厚度增大时,裂纹尖端应力强度因子随之减小,这是由于厚度增大使得结构刚度也增大的缘故.反之,随着蒙皮厚度的增大,结构剩余强度则随之增大.因此,适当地增大蒙皮厚度对结构损伤容限有积极的影响.
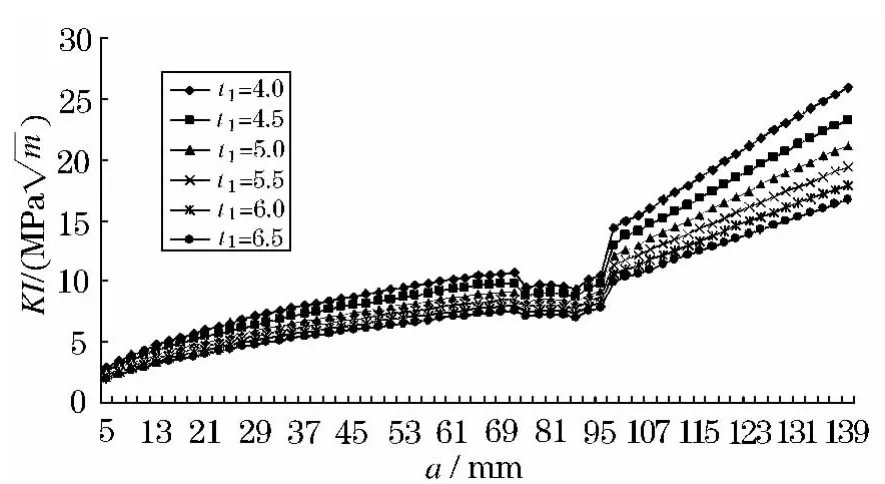
图9 应力强度因子随t1变化曲线
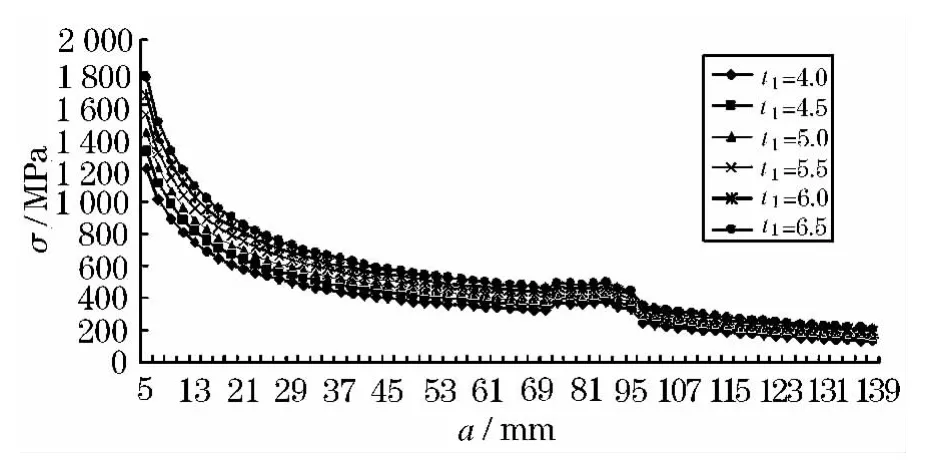
图10 剩余强度随t1变化曲线
分别取t2=2.0、3.0、4.0、5.0、6.0、7.0 mm,其他参数保持不变进行有限元分析.得到t2变化时的蒙皮应力强度因子(图11)和剩余强度曲线(图12).
凸台的厚度对整体壁板的断裂控制也是有比较显著的影响的.与蒙皮厚度的影响一样,在裂纹穿过筋条之前,随着凸台厚度的增加,应力强度因子随之减小.但是,当裂纹穿过凸台以后,应力强度因子基本不受凸台厚度的影响,不同凸台厚度下的应力强度因子几乎相同,这是因为当裂纹穿过凸台后,凸台断开,此时凸台对裂纹尖端应力强度因子的影响就很小了.同样,凸台厚度对结构剩余强度因子的影响在裂纹穿过凸台之前也和蒙皮厚度的影响一样,但是当裂纹穿过凸台后,凸台厚度对剩余强度因子的影响也非常小.
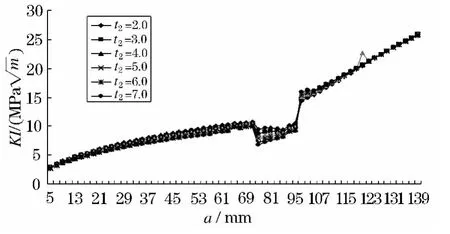
图11 应力强度因子随t2变化曲线
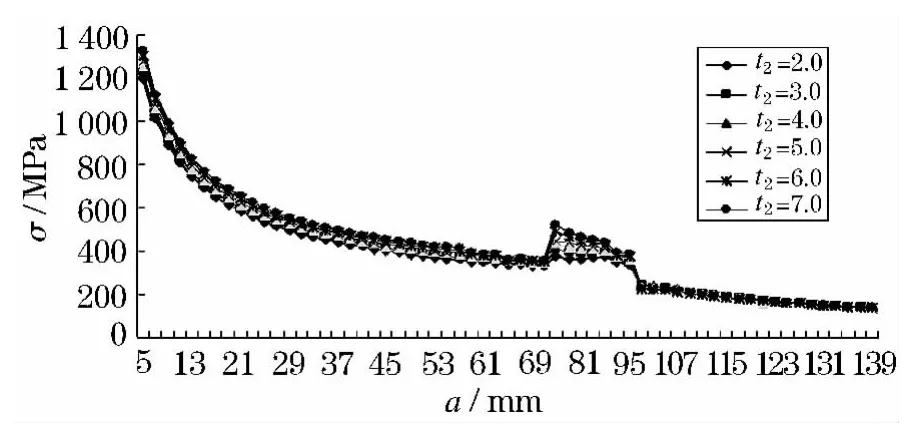
图12 剩余强度随t2变化曲线
分别取L1=20、24、30、40 mm,其他参数保持不变进行有限元分析.得到L1变化时的蒙皮应力强度因子(图13)和剩余强度曲线(图14).
凸台宽度的增大导致整体壁板的截面积增大,所以在壁板长度不变的情况下,截面积增大就表示结构刚度增大,因此,当裂纹穿过凸台之前,蒙皮应力强度因子随着凸台宽度的增大而减小;由于凸台和筋条的止裂作用,裂纹在凸台上扩展时应力强度因子有所减小;当裂纹穿过凸台后,和之前的计算结果一样,凸台宽度对蒙皮应力强度因子和结构剩余强度的影响很小.
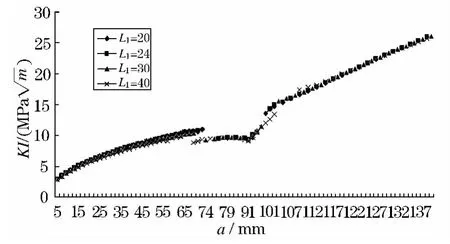
图13 应力强度因子随L1变化曲线
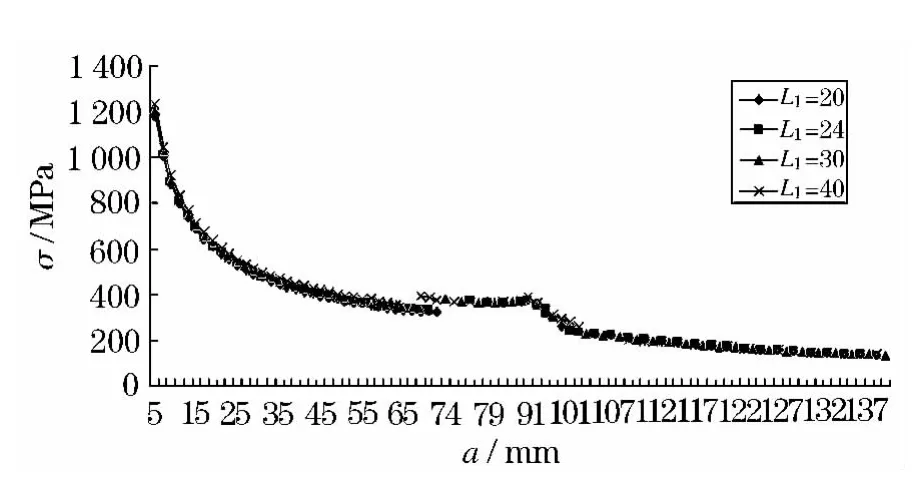
图14 剩余强度随L1变化曲线
由以上对结构的3个重要参数的分析可以得出以下结论:
对于蒙皮应力强度因子及其相应的结构剩余强度,蒙皮厚度的敏感性远远大于其他几何参数;
除了蒙皮厚度外,其他2个结构参数均在裂纹穿过凸台以后对计算结果产生很小的影响.
6 结语
对于本文讨论的整体壁板结构,凸台和筋条的存在明显降低了蒙皮裂纹尖端的应力强度因子,并使得结构剩余强度在局部有所提高.这说明整体壁板上的凸台和筋条有明显的止裂效果.
本文对整体壁板的3个重要结构几何参数进行了简单的敏感性分析.计算结果表明,在不同的参数数值下,应力强度因子呈现有规律的变化,结构剩余强度也因几何参数的变化而变化.在这3个参数中,应力强度因子和其对应的结构剩余强度对蒙皮厚度最为敏感,其次是凸台厚度.
此外,结构刚度的增加主要是因为整体壁板截面积的增加,这就导致了结构重量的增大.所以在结构设计时,要在保证结构性能的前提下尽量减少结构重量,这就需要对结构进行进一步的优化,本文为整体壁板的结构设计提供了良好的参考.
[1]VLIEGER H.Residual strength of cracked stiffened panels[J].Engineering Fracture Mechanics,1973(5):447-478.
[2]GIGLIO M,MANES A.Crack propagation on helicopter panel:Experimental test and analysis[J].Engineering Fracture Mechanics,2008(75):866–879.
[3]CHEN C S,WAWRZYNEK P A,INGRAFFEA A R.Crack growth simulation and residual strength prediction in airplane fuselages[R].NASA/CR-1999-209115;1999.
[4]CHEN Y Z.Tension of finite cracked plate with stiffened edges[J].Engineering Fracture Mechanics,1994,49(5):667-670.
[5]TSAMASPHYROS G,DIMOU G.Stress intensities in a strip reinforced by stiffeners at the edges[J].Engineering Fracture Mechanics,1995,51(6):897-914.
[6]ISIDA M.Effect of width and length on stress intensity factors under various boundary conditions[J].International Journal of Fracture,1971,7(3):301-306.
[7]FOSSATI M,COLOMBO D,MANES A,et al.Numerical modeling of crack growth profiles in integral skin-stringer panels[J].Engineering Fracture Mechanics,2011,78:1341-1352.
[8]曹金凤,王旭春,孔 亮.Python 语言在Abaqus 中的应用[M].北京:机械工业出版社,2011.
[9]ZHANG X,LI Y.Damage tolerance and fail-safety of welded aircraft wing panels[J].AIAA J 2005(43):1613–1623.

