一种适于高光谱图像压缩的相关系数矩阵近似计算算法

洪 恒，何明一

（西北工业大学 电子信息学院，陕西省信息获取与处理重点实验室，陕西 西安 710129）

高光谱遥感成像技术（Hyperspectral Remote Sensing，HRS）作为一种新型遥感成像技术，将二维成像遥感技术与光谱技术有机结合，能够在获取被测物空间信息的同时，获取地物的光谱信息。高光谱图像可以看做在传统二维图像的基础上新增一个光谱维度，这直接导致了高光谱图像数据量庞大的特点，给遥感数据传输和存储带来了挑战。因而，如何对高光谱图像进行有效地压缩是一个非常有意义的课题。常用的高光谱图像压缩算法主要包括基于预测的算法[1]、基于变换的算法[2]和基于矢量量化的算法[3]等。

由于大气吸收等原因，高光谱图像中一些波段与相邻波段的相关性下降，使得在压缩过程中直接采用波段的自然顺序进行处理无法获得理想的压缩效果。针对这种现象，有许多学者提出了相应的预处理方法，如采用自适应聚类的方法进行自适应波段分组，再分别对各组内波段进行压缩[4]，有效提高了压缩性能。还有学者提出先通过比较相邻波段的相关系数进行自适应分组，再对组内波段进行排序的方法[5]，也能提高预测性能。但是这些预处理算法都是以高光谱图像各波段间的相关系数矩阵为基础，而相关系数矩阵所需的计算量非常大，往往计算相关系数矩阵的时间要远远高于预处理算法本身所需的时间，这严重制约了这些预处理算法的实时应用。

文中针对上述高光谱图象压缩中相关系数矩阵计算量过大的问题，提出先对高光谱图像空间域进行适当采样，然后利用采样后图像的相关系数矩阵来代替整幅图像的相关系数矩阵。实验结果证明，该方法在基本保持压缩算法性能的前提下，有效降低了计算量，保证了预处理算法的实时性，是一种简单、有效的实用方法。

1 高光谱图像相关系数矩阵

高光谱图像压缩主要利用了图像像素间的相关性，相关性越强，信息冗余就越多，压缩效果也就越好。而高光谱图像具有空间相关性和谱间相关性两种相关性。空间相关性表现为，各波段中相邻地物的光谱强度存在一定的连续性。谱间相关性包含谱间统计相关性和谱间结构相关性，谱间统计相关性表现为各波段的光谱强度值分布存在相关性，谱间结构相关性表现为各波段图像间存在很强的结构相似性。对于高光谱图像而言，谱间相关性较强，而空间相关性相对较低。为了充分利用高光谱图像的谱间相关性，需要定量地评估波段间的相关性大小，定义波段i 和波段j 之间的相关系数如下：

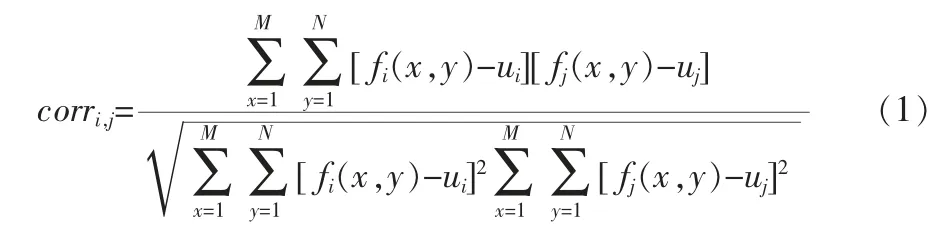
式中，fi（x，y）和fj（x，y）分别代表波段i 图像和波段j 图像在坐标（x，y）处的灰度值，ui和uj分别代表波段i 图像和波段j 图像的像素平均值，M 和N 分别代表图像的长和宽。

可见，所有波段间的相关系数就构成了高光谱图像的相关系数矩阵。图1 是一幅AVIRIS 高光谱图像的相关系数矩阵，其中，相关性越高，其亮度越强，反之则越暗。从该图可以看出，高光谱图像中相邻波段间的相关性很高，非常接近于1。同时存在一些波段与相邻波段的相关性急剧降低，反而与较远处的波段相关性更强，这是由于大气吸收等因素导致地物的光谱特征发生突变引起的结果。相关系数矩阵所反映出的这些波段特征，正是后续处理中对波段进行分组排序的重要依据。

图1 AVIRIS 高光谱图像相关系数矩阵（白色代表1，黑色代表0）Fig.1 Band correlation coefficient image of AVIRIS hyperspectral image（“White”and“Black”denotes correlation coefficient 1 or 0，respectively）

2 相关系数矩阵近似算法

由式（1）可知，相关系数矩阵的计算量巨大。对于一幅长、宽和波段数分别为M、N 和K 的高光谱图像，利用相关系数矩阵的对称性减少一半的计算量之后，直接计算仍然需要5MNK2/2 次加法，3MNK2/2 次乘法，K2/2 次除法和K2/2 次开方运算，难以满足实时性的要求。

首先考虑高光谱图像空间分辨率较高时的情况。当空间分辨率较高时，图像中的一个像素与周围像素会有着较强的相关性，也即意味着这些相似的像素对图像相关系数矩阵的影响也是相似的。因此，可以不必在谱间相关性计算中代入所有的像素值，而是通过对像素进行适当地采样，用采样点来代表其周围的点进行运算。从而可以从一个较小的计算规模中得到一个满意的近似解。然而对于空间分辨率不是很高的高光谱图像而言，图像中一个像素周围的点很可能是其他类别的地物，采样将会丢失一部分的信息。但是在丢失的信息中以空间信息为主，大部分波段信息仍然得到了保留。因而如果该图像的地物变化不是那么剧烈，或者该图像的地物内容不是过于丰富且零散，那么均匀采样后的图像也能够大致保留了原图像所包含的波段特征，仍然能够近似地求解出相对可靠的相关系数矩阵。可见，近似算法具有一定的局限性，但是考虑到它所节约的计算量可以使预处理算法的实时性成为可能，仍是非常有意义的。

因此，文中通过在高光谱图像的空间域进行均匀采样，以得到一幅较小的采样图像，然后利用该图像的相关系数矩阵来近似整幅图像的相关系数矩阵，从而大幅减少了计算量。近似和优化过程如下：

1）对各波段图像每隔L 行L 列进行采样，得到采样后的图像gi（x，y），且长宽分别为M′=⎿M/L」和N′=⎿N/L」，波段数依然为K。

2）计算各波段均值：

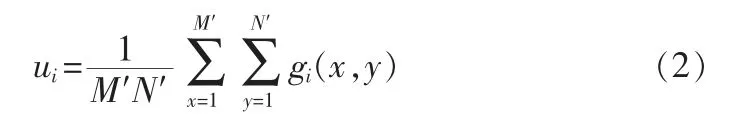
3）归一化：

4）计算临时变量：

5）计算近似相关系数：

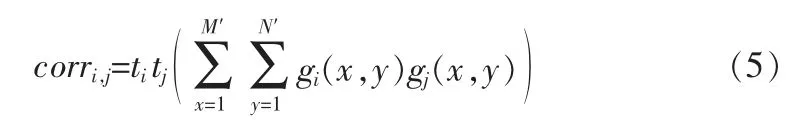
依据文中提出的相关系数矩阵近似计算方法，则计算量减少到MNK2/2L2次加法，MNK2/2L2次乘法，2K次除法，K次开方运算，其中L为采样步长。直接计算量与近似算法计算量之比见表1，效果非常显著。

表1 相关系数矩阵计算量Tab.1 Calculation cost of correlation matrix

实验结果表明，在一定范围内L 的取值对算法性能影响不大，可以根据具体实际应用的实时性要求，对L 进行适当取值。若选取L=32，对于一幅长、宽和波段数分别为512、512 和200 的高光谱图像，即M=N=512，K=200，直接法与近似法计算相关系数矩阵的加法、乘法、除法以及开放运算计算次数之比分别为5 120，3 070，50 和100，详见表2。显然，近似算法对于相关系数矩阵计算量的减少是非常可观的。

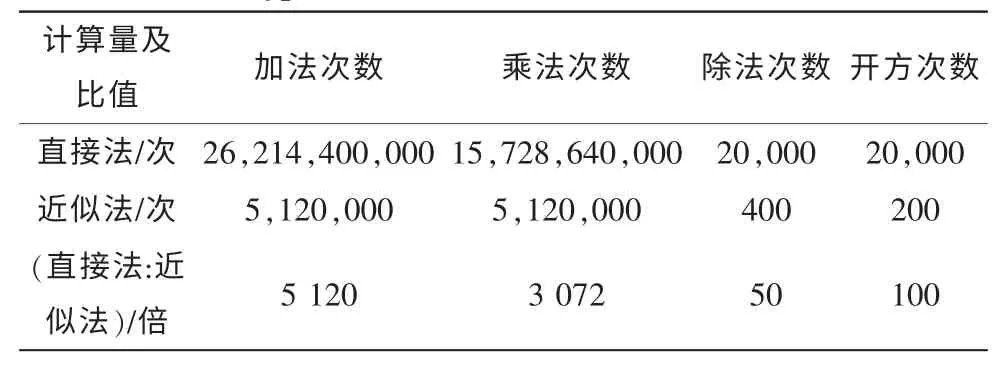
表2 相关系数矩阵典型计算量Tab.2 Typical calculation cost of correlation matrix

3 实验结果

实验采用的高光谱遥感图像来自于NASA/JPL 实验室研制的AVIRIS 成像仪于2006年获取的经辐射数据校正的Yellowstone 图 像（http：//compression.jpl.nasa.gov/hyperspectral/）。该图像为最新发布的标准测试图像，采用新的校准技术，避免了1997年标准测试图像中存在过多校准引起的人为影响。该传感器波长范围为450～2 500 nm，光谱分辨率约10 nm，共包含224个波段。一组Yellowstone 图像包含5 幅图片，每幅图片大小为512×677×224，每个像素16 位。图3为 各 幅Yellowstone 场景中第70 波段的灰度图像。实验的测试平台为ASUS PC（Intel Core i3-2310M 2.1 GHz，6G 内存），工作环境为Window7，编译环境为Visual Studio C++2010。

图2 实验用高光谱图像Fig.2 hyperspectral images in test

为验证相关系数矩阵近似算法的有效性，分别比较不同采样步长下近似算法对高光谱图像压缩算法最终压缩性能的影响。实验采用的高光谱压缩算法，首先根据相关系数矩阵采用最小生成树算法[6]优化波段预测顺序，然后利用三维上下文模型[7]进行谱间预测，熵编码采用算术编码。实验分别选取采样步长L=1，2，4，8，16，32，64 进行相关系数矩阵的近似计算（其中L=1 即为原始算法），并比较最终压缩算法的压缩比，结果如表3 所示。实验结果表明，在一定范围内采样步长的提高几乎不影响算法的压缩性能。然而当采样步长过大时，将因为采样点过少而导致相关系数矩阵严重失真，使得算法的性能明显退化。综合以上考虑，本文选取采样步长L=32，此时算法性能损失不大，同时计算量不到原来的千分之一，有效降低了计算负担。表4 具体地给出了在测试平台下，一幅AVIRIS高光谱图像的相关系数矩阵采用近似算法前后的计算量对比和运行时间对比。可见，采用近似算法后，预处理过程的计算量大幅降低，运行时间大幅减少，有效提高了算法的实时性。

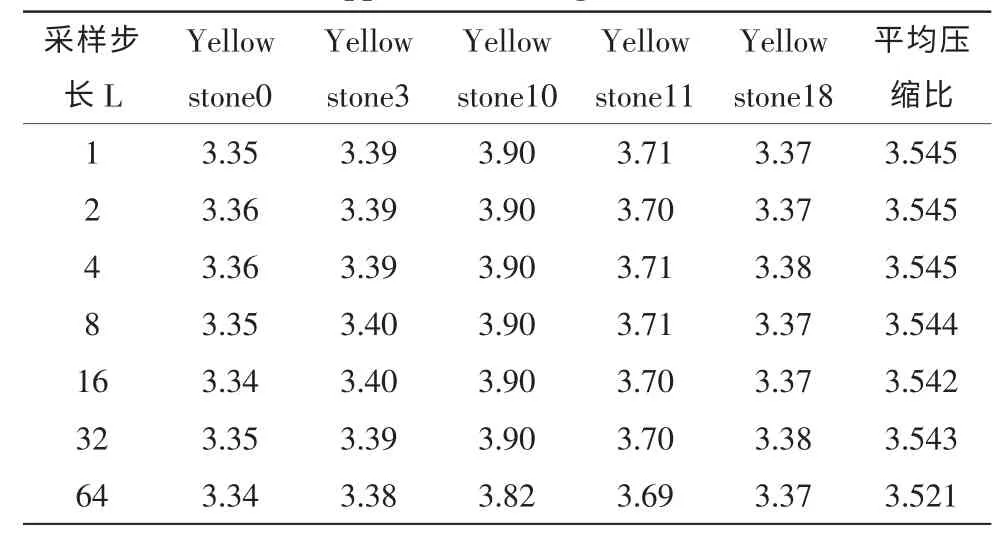
表3 近似算法中不同采样步长下的压缩性能Tab.3 Compression ratio using different sample step in approximation algorithm

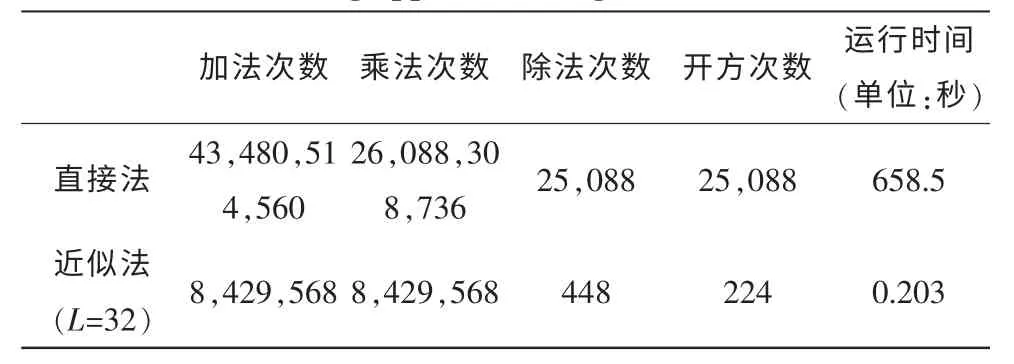
表4 采用近似算法前后相关系数矩阵计算量Tab.4 Calculation cost of correlation matrix（before and after using approximate algorithm）

另外值得注意的是，存在个别图像采用某些步长下的近似算法后，其压缩性能与原始算法相比没有降低反而还有少量的提升。经过观察验证，发现这是由于相关系数与压缩性能并不完全对应所照成的。存在着一些波段一方面与一个波段相关性最高，另一方面最优的参考波段又是另一个波段，如图像Yellowstone0 中与波段1 相关性最高的为波段2，但是实验数据显示以波段168 来预测波段1 得到的压缩比更高，但是这样提高的压缩比往往是非常微弱的。同样的情况也出现在近似算法中，由于近似算法的退化，导致后续压缩算法在选择参考波段时选择了实际相关系数次优的波段，但结果反而少量提高了预测波段的压缩性能。但是总体而言，相关系数与压缩比存在着一种正相关的关系，同时不像残差熵、均方误差这些指标那样需要先对图像进行预测才能得到，因而相关系数依然是目前较为理想的预测压缩性能的指标。同时，对于是否有更好的预测压缩性能的方式，也是往后开展工作的一个方向。

4 结论

文中针对高光谱图像压缩过程中，波段预处理算法普遍使用的相关系数矩阵计算量过大的问题，提出一种基于空间域采样的近似算法。实验结果表明，适当选取采样步长能在几乎不影响压缩算法性能的情况下，大幅降低计算量，使得预处理算法的实时应用成为可能，是一种简单、有效的实用方法。

[1]Mielikainen J，Huang B.Lossless compression of hyperspectral images using clustered linear prediction with adaptive prediction length[J].Geoscience and Remote Sensing Letters，IEEE，2012，9（6）：1118-1121.

[2]陈雷，张晓林，杨维松，等.一种基于预测和变换混合设计的超光谱图像压缩方法[J].航空学报，2010（4）：754-761.CHEN Lei，ZHANG Xiao-lin，YANG Wei-song，et al.A hyperspectral image compression method based on hybrid predictive coding and transform coding[J].Acta Aeronautica et Astronautica Sinica，2010（4）：754-761.

[3]温佳，马彩文，水鹏朗.改进自适应LBG矢量量化算法在干涉高光谱图像压缩中的应用[J].光谱学与光谱分析，2011（4）：1033-1037.WEN Jia，MA Cai-wen，SHUI Peng-lang.An adaptive VQ algorithm used in interferential multi-spectral image [J].Spectroscopy and Spectral Analysis，2011（4）：1033-1037.

[4]HE Ming-yi，BAI Lin，DAI Yuc-hao，et al.Band regroupingbased lossless compression of hyperspectral images[J].Journal of Applied Remote Sensing，2010，4（1）：041757-041757.

[5]ZHANG Jing，LIU Gui-zhong.An efficient reordering prediction-based lossless compression algorithm for hyperspectral images[J].Geoscience and Remote Sensing Letters，IEEE，2007，4（2）：283-287.

[6]Ellis Horowitz.数据结构基础[M].朱仲涛，译.北京：清华大学出版社，2009.

[7]HE Ming-yi，BAI Lin，DAI Yu-chao，et al.Hyperspectral image lossless compression algorithm based on adaptive band regrouping[C].Satellite Data Compression，Communication，and Processing V.2009.San Diego，CA，United states：SPIE，2009，7455：745504.