大扰动下的船舶电站暂态仿真分析
韩 旗
(海军驻704所军事代表室,上海 200031)
大扰动下的船舶电站暂态仿真分析
韩 旗
(海军驻704所军事代表室,上海 200031)
针对目前在船舶电站暂态稳定分析中普遍采用的仿真工具MATLAB/Simulink算法受限且仿真时间过长的不足,应用时域仿真法建立船舶电站的数学模型,再用基于隐式梯形积分法的C#.NET程序对其求解。通过对仿真结果的分析验证了仿真方法的有效性。
船舶电站;大扰动;暂态;C#.NET;隐式梯形积分法
0 引言
目前,国内外求解船舶电力系统仿真模型普遍利用MATLAB/Simulink丰富的电力系统模块进行仿真计算[1],这种方法减轻了人工编写程序的负担也简化了仿真的过程,但它不能完整如实地反映系统的数学建模过程。本文用C#.NET语言编写基于隐式梯形积分法程序,解出构成模型的非线性微分代数方程组的数值解,用计算机语言编程的方法不仅方便我们随时修改模型和模型参数,模型的阶数还可以自由决定,为本文建立发电机七阶模型奠定了基础。
目前,微分代数方程组的求解方法大致来说有改进欧拉法、龙格-库塔法、隐式梯形积分法等,而隐式梯形积分法相对于其它方法数值稳定性和精度较高,因此得到广泛应用[2]。
1 船舶电站数学建模
船舶电站的非线性微分代数方程组包含同步发电机方程、柴油机及其调速系统方程、励磁系统方程和负荷方程。同步发电机方程又可拆分为描述电磁暂态过程的电磁回路方程和描述机电暂态过程的转子运动方程,如图1所示。
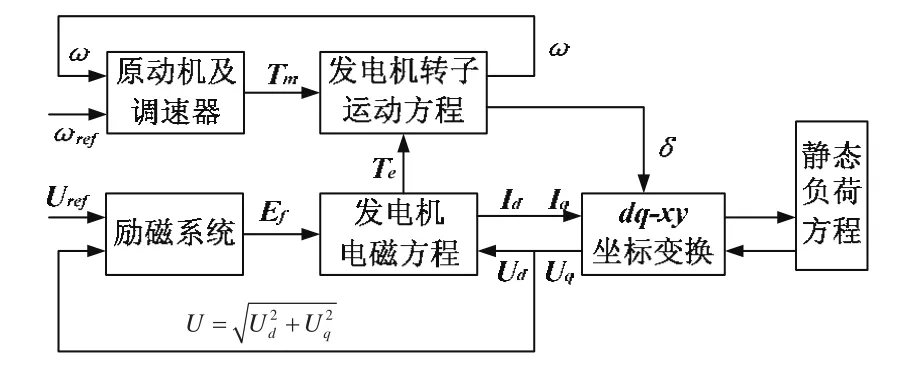
图1 船舶电力系统组成示意图
到目前为止,很多文献忽略船舶电网相对于陆地大电网的特殊性,采用陆地无限大电网常用的发电机降阶模型,不考虑转速变化和定子暂态,这在系统暂态分析时会有一定误差[3],在对船舶电站所带负荷突增和突卸时的仿真时,会引起更大的误差,所以这种用简化过的方式建立动态仿真模型已经反映不了船舶电站的实际状态,有必要建立同步发电机的七阶数学模型。
1.1 同步发电机建模
本文建立的发电机七阶数学模型,考虑到了定子绕组暂态过程和阻尼绕组D、Q以及励磁绕组暂态过程和转子动态过程,它是在dq0坐标系下建立的数学模型,适于研究船舶电力系统各种物理问题[1]。
经过派克变换后的磁链方程(标幺值形式)为:
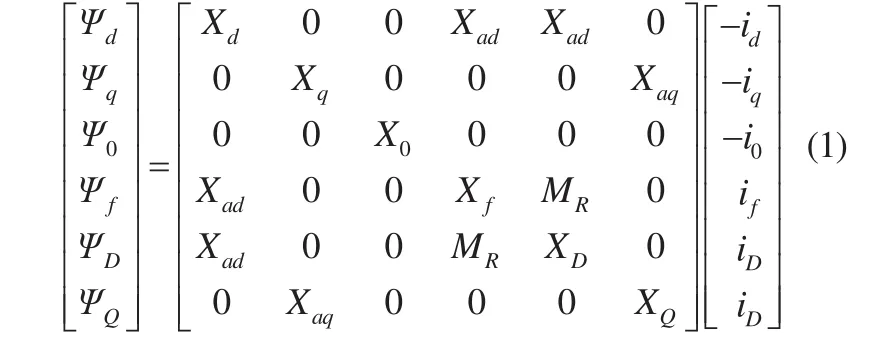
经过派克变换后的电压方程(标幺值形式)为:
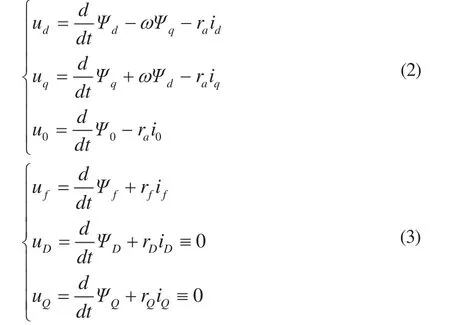
为了推导七阶数学模型,必须定义以下几个中间量:电机q轴空载电势:

电机q轴暂态电势:

定子励磁电势:

电机d轴次暂态电势:
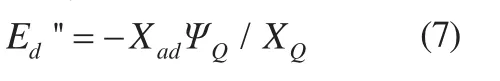
电机q轴次暂态电势:

1)定子电压方程
定子电压方程由式(2)和(3)变换所得:

其中,磁链表达式为:

2)转子f绕组电压方程
由式(5)、式(6)代入方程式(3)可得:
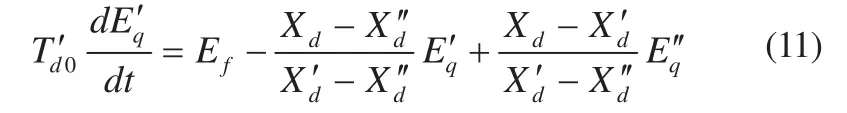
3)转子D绕组电压方程
将式(4)、式(8)代入式(3)、式(5)得到:
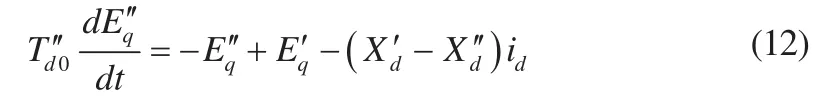
4)转子Q绕组电压方程
由式(1)变换可得:
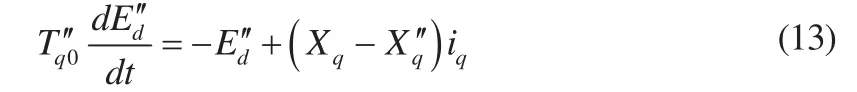
5)转子运动方程

式(9)与式(10~14)共同构成七阶同步发电机数学模型。
1.2 柴油机及其电子调速系统数学建模
当柴油发电机组运行时,一旦负荷发生变化,发电机组运行的稳态就会被打破,导致发电机加速或者减速[4]。根据达兰贝尔原理:
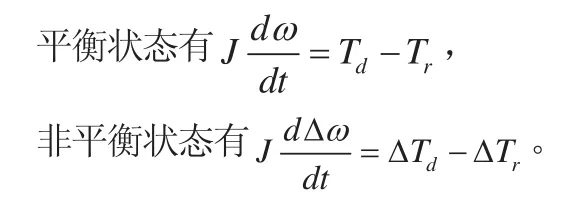
式中,J为转动惯量;ω为转速;Td为驱动力矩,Td=f(w , fi);Tr为阻力矩;fi为喷油量。对于非增压型柴油机而言,它的驱动力矩可看为关于柴油机转速ω与喷油量fi的函数。以下是把Td按照泰勒级数展开:
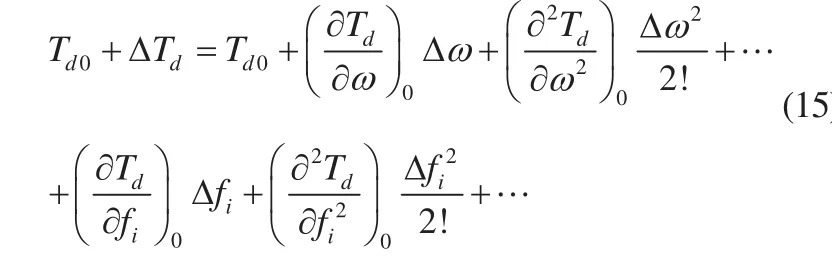
无调速系统柴油机当油门开度不变时有:
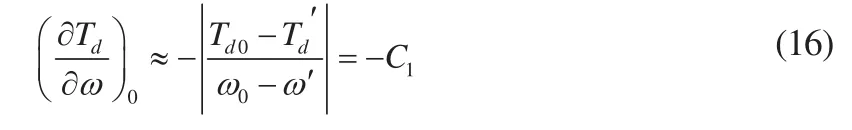
式中C1为常数,可查柴油机手册。转速不变时,fi与Td的关系为:

由式(15~17)得到柴油机在非平衡状态下的数学模型:
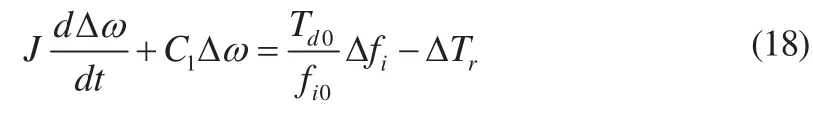
式(18)中 Δfi可看为调速系统输出,即油门开度,电子调速系统的输入为转速偏差信号Δω,那么加入PID环节的电子调速系统的数学模型应为:
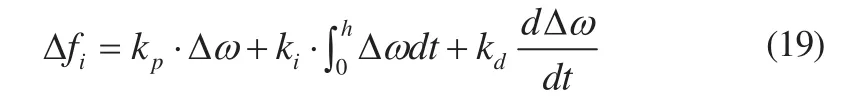
式中,h为仿真步长。综合式(18)得到最终的柴油机及其电子调速系统数学模型:
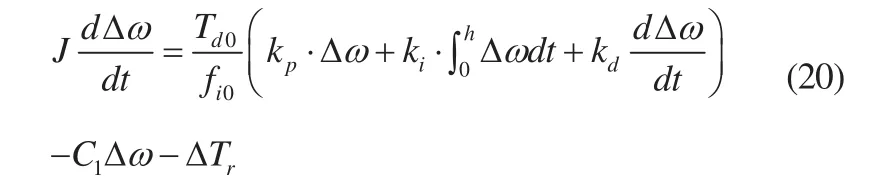
1.3 励磁控制系统数学建模
励磁控制系统起着调节电压、保持发电机端电压恒定的作用,并且可以控制并联运行的发电机无功分配[1]。下面以自并励静止励磁系统为例建立数学模型[5],如图2所示。
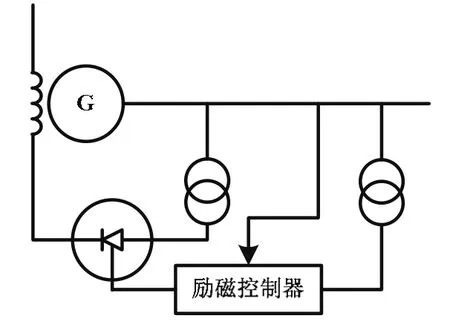
图2 自并励静止励磁系统
半可控全波整流电路中,励磁电压Ef与导通角α有关,即:

端电压U的调节是通过励磁控制系统直接改变α的大小,从而改变励磁电压和电流实现的。将发电机端电压的偏差信号作为输入,得到的励磁电压公式为:
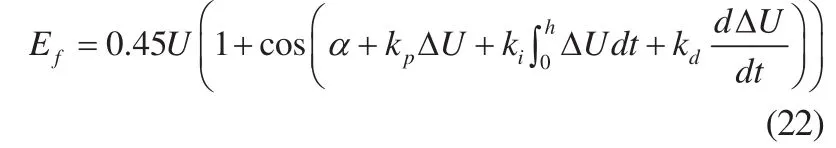
1.4 暂态稳定的船舶电站数学模型
将以上各部分模型的方程组相结合,得到的就是暂态稳定的船舶电站数学模型:

负荷模型就是恒阻抗的模型,它的电阻和电抗值在某一时刻发生突变,以此来模拟电站受到大的扰动。
2 时域仿真法求解数学模型
2.1 隐式梯形积分法原理
用数值算法求解数学模型的过程,实质是在一定的初值条件下,求微分方程数值解,该过程也就是对于离散的时间序列t0,t1,…,tn逐步求出相应的系统状态矢量值y0,y1,…,yn的过程,所以隐式梯形积分法又称逐步积分法[1]。
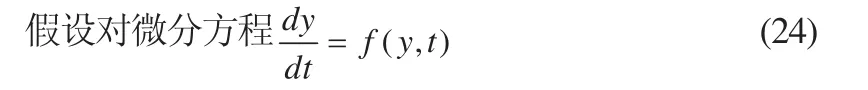

在实际的计算时我们需要对其中的积分项作近似计算。若取

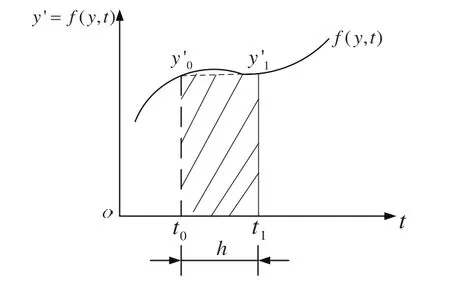
图3 隐式梯形积分法原理图
隐式梯形积分法相应的通用计算公式为:
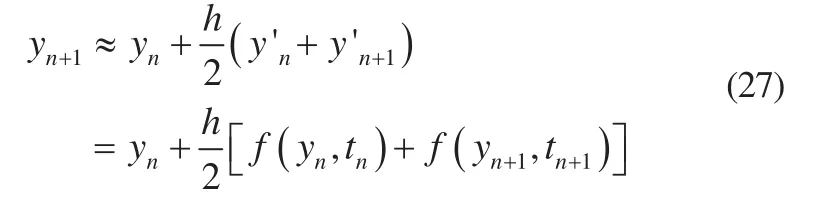
这是一个关于yn+1的非线性差分代数方程,且方程中的参数随时间变化而变化。
2.2 隐式梯形积分法暂态方程
在用隐式梯形积分法求解本文所建立的船舶电站数学模型时,首先要将其微分方程组化为差分方程,得到隐式梯形积分法的暂态方程。
1)发电机转子绕组暂态方程
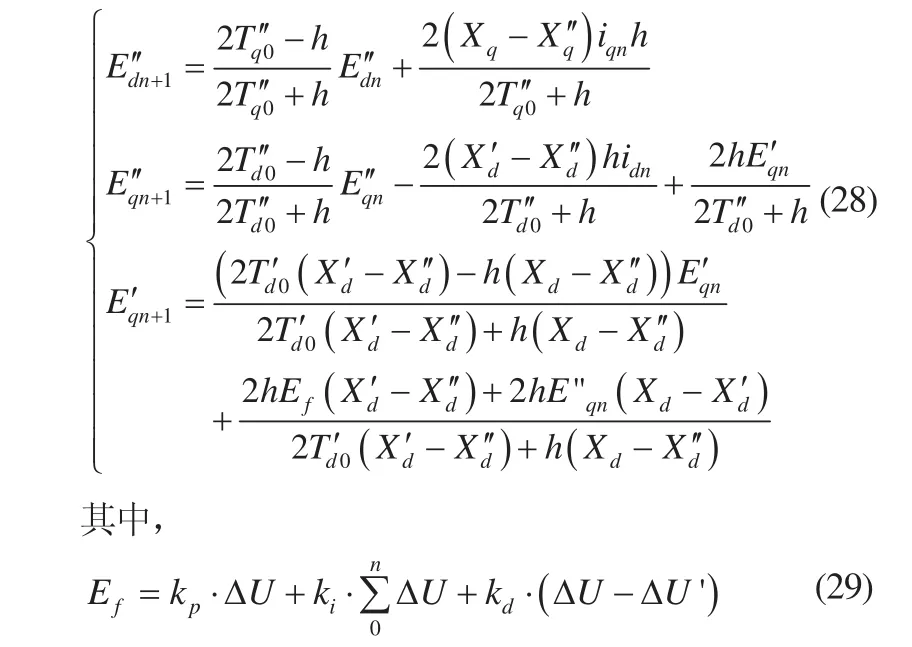
2)发电机定子绕组电压方程

3)发电机转子运动方程
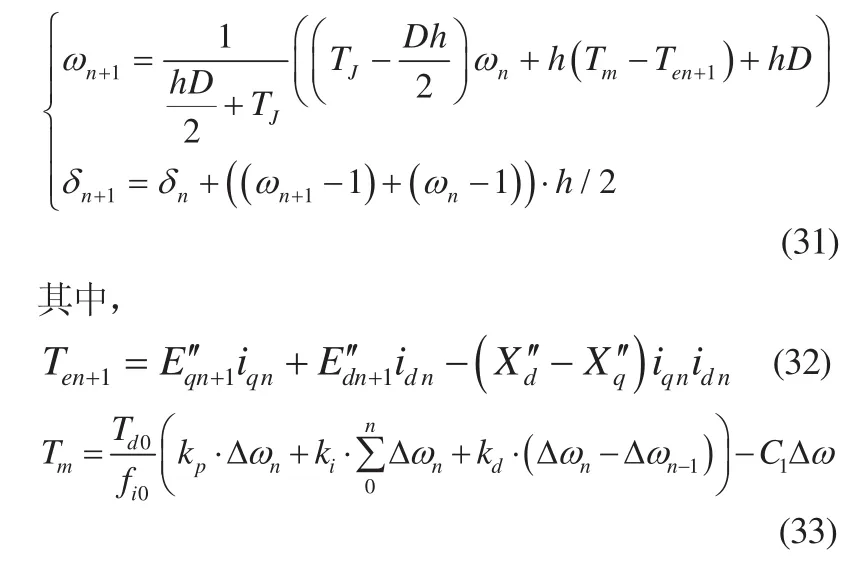
2.3 隐式梯形积分法求解流程
根据暂态稳定的船舶电站数学模型和隐式梯形积分法求解数学模型的原理,得到求解流程,如图4所示:
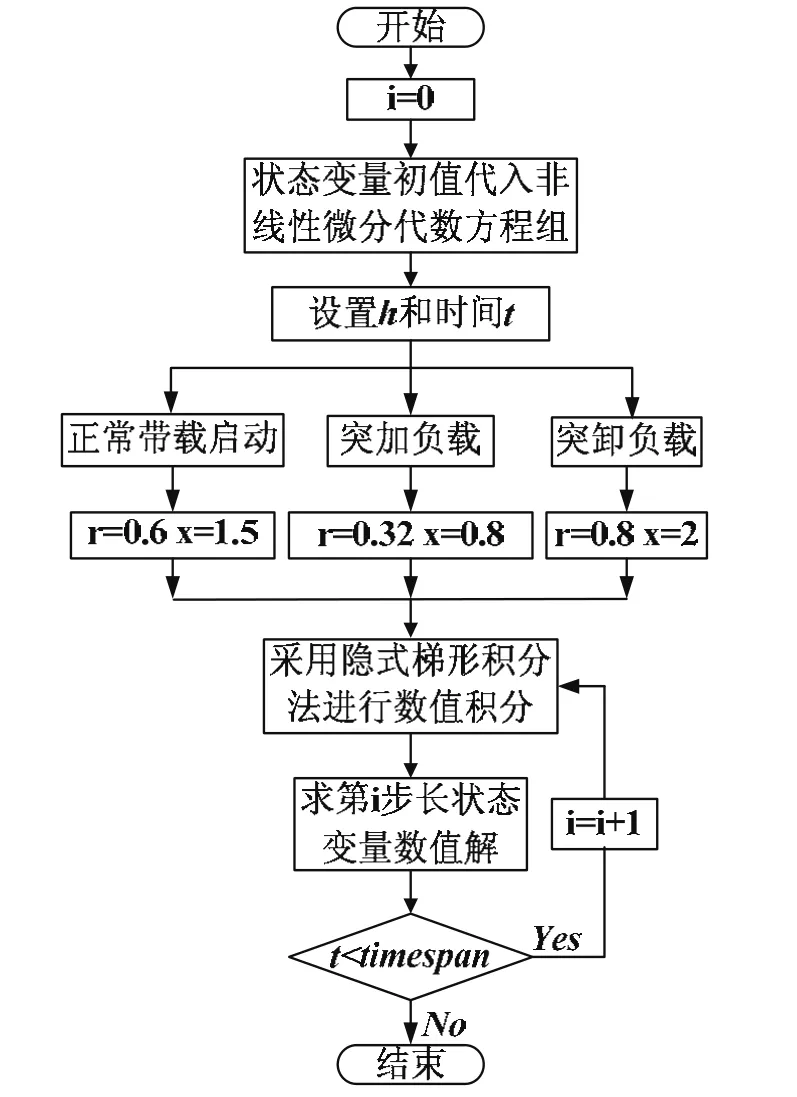
图4 隐式梯形积分法求解流程
根据该流程编写的隐式梯形积分法的 C#.NET程序[6],在确定了仿真步长、总时间以及各运行状态对应的负荷阻抗值后,进行数值积分,每一步迭代产生的是状态变量在当下步长的数值解,最后完成数学模型的求解。
3 仿真算例与结果分析
程序将仿真结果存入Excel表格后再用MATLAB调取仿真得到的数据,绘制成各个变量的曲线。仿真时间为10s,步长为0.005s。扰动前后电阻和电抗的值在图4中给出。4s时加入扰动,仿真算例的主要参数见表1所示(标幺制)。算例中,系统突增 46.8%的负荷,仿真结果如图5~7所示。

表1 仿真算例主要参数
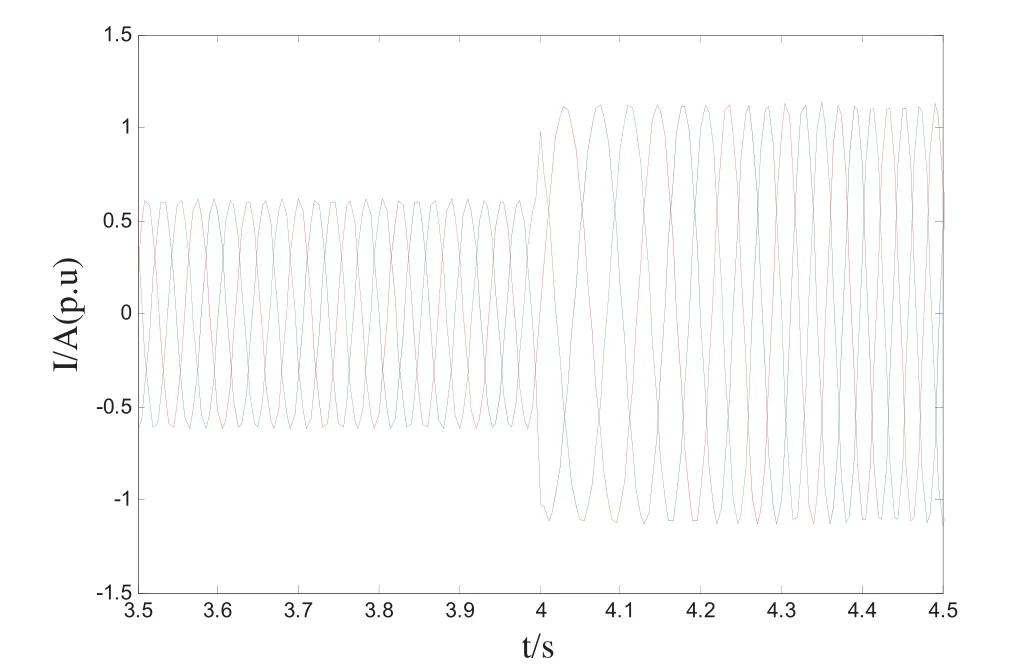
图5 扰动前后的三相负荷电流
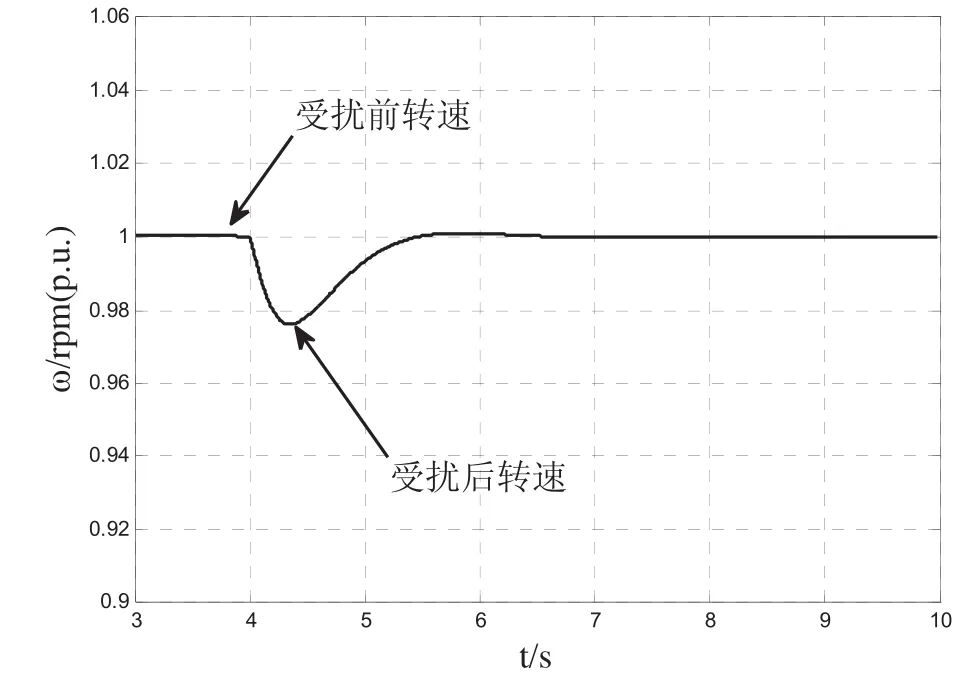
图6 扰动前后的发电机转速

图7 扰动前后端电压
图5 ~7给出了突增负荷前后的三相负荷电流、发电机转速以及发电机端电压的曲线,扰动前的负荷阻抗为r=0.6,x=1.5,扰动后的为r=0.32,x=0.8,阻抗比始终为0.4。突增负荷时的电压瞬态变化率为7.6%,1.3s后稳定;瞬态调速率为 2.4%,1.4s后稳定。结果都在《钢质海船入级与建造规范》规定的范围内[7]。
4 结论
本文建立了船舶电站的高阶非线性数学模型,并用隐式梯形积分法的C#.NET程序求解方程组,通过对仿真结果的分析验证了算法的有效性。
[1] 陆超, 唐义良, 谢小荣, 崔文进. 仿真软件 MATLAB PSB与PSASP模型及仿真分析[J]. 电力系统自动化,2000, 24(9): 23-27.
[2] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[3] 李东辉, 张均东, 何治斌. 教学实习船电力系统建模与仿真[J]. 上海交通大学学报, 2008, 48(2): 190-193.
[4] 刘雨. 船舶柴油发电机组的建模与智能控制的仿真研究[D]. 大连: 大连海事大学, 2002.
[5] 区干生. 基于 DSP的微机励磁调节器的设计与实现[D]. 武汉: 华中科技大学, 2004.
[6] Karli Watson, Christian Nagel. C#入门经典(第三版)[M]. 北京: 清华大学出版社, 2006.
[7] 中国船级社.钢质海船入级与建造规范[M]. 北京: 人民交通出版社, 2008.
Transient Stability Analysis of Shipping Power Station After Large Disturbance
HAN Qi
(Navy Representative Office Stationed at No. 704 Research Institute, Shanghai 200031, China)
Aiming at the disadvantage of current time-consuming MATLAB/Simulink, nonlinear mathematical models of shipping power station are established by using time domain simulation. Implicit Trapezoidal Integration Method is then selected to solve the equations by C#.NET program. Finally, the results measure up to criterion which proves the advantage of this method.
shipping power station; large disturbance; transient stability; C#.NET; Implicit Trapezoidal Integration Method
TM712
A
韩旗(1970-),男,高级工程师。研究方向:电气及自动化。

