应用Actigraph三轴加速度传感器矢量计数监测日常体力活动的研究

向剑锋，李之俊

研究证实，体力活动不足是肥胖、糖尿病等慢性疾病的重要致病因素，加强体力活动的监测与干预是增强体质、预防疾病的有效措施。加速度传感器是一种便携、准确的运动传感器，可测得人体活动时的加速度计数（Activity Counts，AC），从而间接推算体力活动能耗和低、中、高强度体力活动的时间。加速度传感器已被广泛应用于欧美发达国家的体力活动研究中，取得了良好的效果［17］。在早期的研究中，美国Actigraph公司生产的单轴加速度传感器应用最广。近年来，Actigraph公司研发了GT3X、GT3X＋、Actitrainer等多款三轴加速度传感器，可同步监测活动中的垂直轴 AC（ACz）、冠状轴 AC（ACx）和矢状轴 AC（ACy），并转换为水平轴计数（horizontal AC，ACh）和综合的矢量计数（Vector Magnitude，VM）［10］。ACh计算方法为:ACh＝（ACx2＋ACy2）1／2。VM 计算方法为:VM＝（ACx2＋ACy2＋ ACz2）1／2。

由于三轴加速度传感器可监测到更丰富的体力活动数据，Actigraph三轴加速度传感器逐渐成为监测体力活动的主流加速度传感器，但以该传感器的VM为自变量进行体力活动监测的研究相对滞后。目前，仅Sasaki等［22］在2011年曾以VM为自变量为该传感器建立了推算体力活动的绝对能耗（单位:kcal／min）和相对能耗（单位:METs）的预测方程，本研究将其分别简称为S-kcal方程和SMETs方程。随后，该传感器的配套软件Actilife将S-kcal方程与Williams所建的以ACz为自变量的能耗方程（简称W-Kcal方程）组成了一个联合方程（简称Actilife联合方程）供研究人员选用（表1）［6］。Sasaki等［22］还根据 S-METs方程推算出3METs、6METs和9METs所对应的以VM临界点（简称临界点S），分别为2690counts／min、6167 counts／min和9642counts／min。上述方程和临界点在我国成人日常体力活动监测中的效度尚未得到验证。

表1 以VM为自变量的Actigraph加速度传感能耗预测方程一览表Table 1 VM Energy Expenditure Prediction Equations of Actigraph Tri-axial Accelerometer

有学者［5，17，27］认为，传感器的效度与被测试者的体质特征和日常体力活动方式等因素有关。提示，国内研究在使用Actigraph三轴加速度传感器之前，有必要对其效度进行全面验证，或针对特定人群建立新方程和临界点。因此，本研究在借鉴国内、外多个同类研究的基础上，以Actigraph三轴加速度传感器为仪器，以我国青年人群为实验对象，采用多种日常体力活动的实验方案及ROC曲线等方法，建立了新的以VM为变量的能耗预测方程和临界点，并以连续4h日常体力活动对Sasaki［22］及本研究所建的方程和临界点进行验证，以确定适合我国青年人的VM能耗预测方程和VM临界点，从而为今后更好地应用Actigraph三轴加速度传感器开展我国国民体力活动研究提供依据。

1 研究对象与方法

1.1 研究对象

受试者为80名在校非体育专业大学生，随机划分为实验组（男、女各30人）和验证组（男、女各10人），两组受试者的人体测量特征无显著性差异（P＞0.05；表2）。受试者身体健康，自愿参加本研究，并于实验前签署知情同意书。受试者实验前一天无大强度体力活动，所有测试均在餐后1h后进行。

表2 本研究受试者人体测量特征一览表Table 2 The Anthropometry Characteristics of Participant（D）

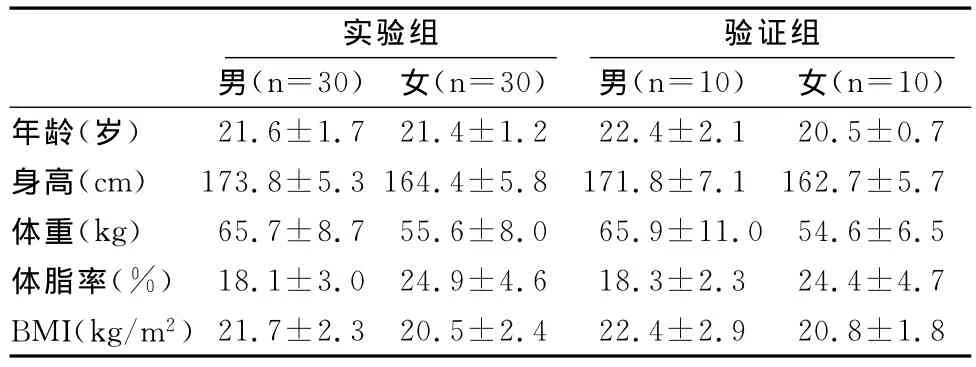
表2 本研究受试者人体测量特征一览表Table 2 The Anthropometry Characteristics of Participant（D）

实验组 验证组男（n＝30） 女（n＝30） 男（n＝10） 女（n＝10）年龄（岁）21.6±1.721.4±1.222.4±2.120.5±0.7身高（cm） 173.8±5.3164.4±5.8171.8±7.1162.7±5.7体重（kg） 65.7±8.755.6±8.065.9±11.054.6±6.5体脂率（%） 18.1±3.024.9±4.618.3±2.324.4±4.7 BMI（kg／m2）21.7±2.320.5±2.422.4±2.920.8±1.8

1.2 研究方法

1.2.1 测量仪器

使用大学生体质测试专用的身高体重计测量受试者身高（cm）和体重（kg），精确到0.1cm（或kg）。使用芬兰产的Polar T31型心率表监测受试者HR。使用韩国产Inbody 3.0体成分分析仪测量受试者体脂率。

使用美国产Actigraph GT3X加速度传感器（简称GT3X）监测受试者的体力活动。GT3X是目前应用最广的三轴加速度计，重量为27g，体积为3.8cm×3.7cm×1.8cm，内存为16MB，电池续航时间为20天，采样范围为0.05～2.5g’s，采样频率为30Hz，处理数据时仪器内部过滤器的采样频率范围为0.25～2.5Hz。实验中统一将GT3X用弹性腰带固定在受试者右侧髋部、肚脐水平高度。GT3X的校对、设置及数据处理等工作在配套的Actilife 6.0软件中进行。体力活动监测前统一将GT3X采样时间设为5s。

以间接测热（Indirect calorimetry，IC）法实时监测受试者的体力活动能耗并作为参考标准，使用的仪器为Cosmed K4b2气体代谢能耗分析仪（简称K4b2）。为保证测量的准确性，每日测试前都要先对K4b2进行预热和校正。实验中，测试人员看准电脑时间中某一分钟第一秒按压K4b2主机上的“Enter”键开始正式测试，以确保每分钟内GT3X和K4b2所获得的监测数据都保持同步。

1.2.2 测试方案

所有测试均在8∶00～12∶30和13∶00～17∶30进行，测试场地安排在综合训练馆内，温度范围为18℃～25℃，湿度范围为50%～80%。受试者身着轻便运动服参加测试，首先进行身高、体重和体脂率的测量，在佩戴、熟悉仪器并通过K4b2的预测试后开始正式测试。

正式测试中实验组受试者需依次完成7项体力活动，其中，非走／跑类活动包括静坐、看书（坐姿）、整理书桌（站姿）和扫地，走／跑类活动包括场地上慢走（4km／h）、快走（6km／h）和慢跑（8km／h）。非走／跑类活动都在综合训练馆的办公室内进行。静坐时，受试者采用舒适的坐姿，心情平静，身体放松。看书时，受试者在书桌旁以平日的状态进行阅读，看书时可适当写字，也可有自然的姿势变化动作。整理书桌时，受试者以站姿将3～5张书桌上杂乱的书籍杂物等东西清理整齐，在调整身体位置时可随意走动。扫地时，工作人员事先在约50m2地面上撒上碎纸屑等杂物，受试者模拟平日扫地的状态进行清扫。

走／跑测试中，预先用标志物在体育馆内设置椭圆形跑道，跑道周长为300m，每5m放置一个标记物。测试时播放相应的节拍，受试者以自然步态匀速前进，节拍每响1次受试者走（或跑）完5m，速度稍慢或稍快时根据节拍和标记物调整速度。在进行正式步行和跑步测试前需先在工作人员的示范下熟悉节拍和速度，正式测试时工作人员也会对受试者进行提醒，使其速度始终与实验要求保持一致。

静坐时间为10min，取其中第3～9min的数据录入数据库；其余每项体力活动各进行6min，取其中第4～6min的数据进行分析［12］。在中、高强度体力活动之间可休息1～5min，以HR恢复到接近静坐HR为宜（两者差值＜10次／min）。

验证组受试者需进行连续近4h体力活动，以检验加速度传感器在长时间日常体力活动监测中的效度。首先，验证组受试者需填写一周体力活动调查问卷，研究人员根据问卷调查结果计算每人一周内各项体力活动（睡觉除外）时间所占比例，依照该比例将每位受试者一周中最主要的12～15种体力活动组成近4h的综合体力活动。随后，验证组受试者同步佩戴K4b2、Polar表和GT3X连续进行约4h体力活动。由于K4b2的电池续航时间仅为2h，研究人员每2h中断1～2min为仪器更换电池，更换电池期间的数据不纳入数据库。在实际研究过程中，受试者连续体力活动的总时间为235.45±2.76min（230～240 min）。所有受试者均顺利完成了上述测试。

1.2.3 数据统计

数据处理时，首先在仪器的配套软件中将K4b2和GT3X测得的原始数据都转换为以“1min”为采样时间的数据，再将两仪器每分钟数据一一对应进行分析。由于受试者背负的仪器总重量约为1kg，因此，特对K4b2输出的每分钟的kcal和 METs进行校正，校正方法为［25］:

校正后能耗＝IC法能耗测试值×原始体重／（原始体重＋1kg）。

使用SPSS 15.0统计软件对数据进行分析处理。以Pearson相关分析法分析GT3X数据与K4b2数据之间的相关性，以逐步回归法建立体力活动能耗预测方程，以配对t检验和Bland-Altman分析图比较方程的能耗预测值与IC法测试值之间的差异。统计分析中显著性水平定义为P＜0.05，高度显著性水平定义为P＜0.01。

以接受者工作特征（Receiver Operator Characteristic，ROC）曲线法建立3METs、6METs所对应的VM临界点。体力活动强度的等级划分方法:0～2.99METs为低强度体力活动（light physical activity，LPA），3～5.99METs为中等强度体力活动（moderate physical activity，MPA），6METs以上为高强度体力活动（vigorous physical activity，VPA），3 METs以上统称为中高强度体力活动（moderate and vigorous physical activity，MVPA）。为了使临界点更好地判断体力活动强度，从而准确地分析低、中、高强度体力活动的时间，本研究确定ROC曲线法的数据来源为:1）在实验组原始数据中，由于≥3METs的数据共有585个，特在＜3 METs的数据中选取最接近3METs的585个数据，共同组成1170个数据以建立3METs所对应的VM临界点；2）同理，由于≥6METs的数据共有186个，特在＜6 METs的数据中选取最接近6METs的186个数据，共同组成372个数据以建立6METs所对应的VM临界点。确定临界点的标准:1）曲线下面积（AUC）＞0.7；2）特异性等于敏感度［3］。

2 研究结果

2.1 实验组体力活动的能耗和AC特征分析

按照本研究中的体力活动顺序，活动的能耗和强度逐渐增加，受试者的HR和AC也同步增加。整理书桌和扫地时ACz明显低于ACh，快走和中速跑阶段ACz明显高于ACh。可见，不同类型、不同强度体力活动的AC特点存在明显差异（表3）。

表3 本研究实验组7项体力活动的能耗、心率和加速度计数一览表Table 3 Energy Expenditure，HR and AC of 7Activities of Development Group （D）

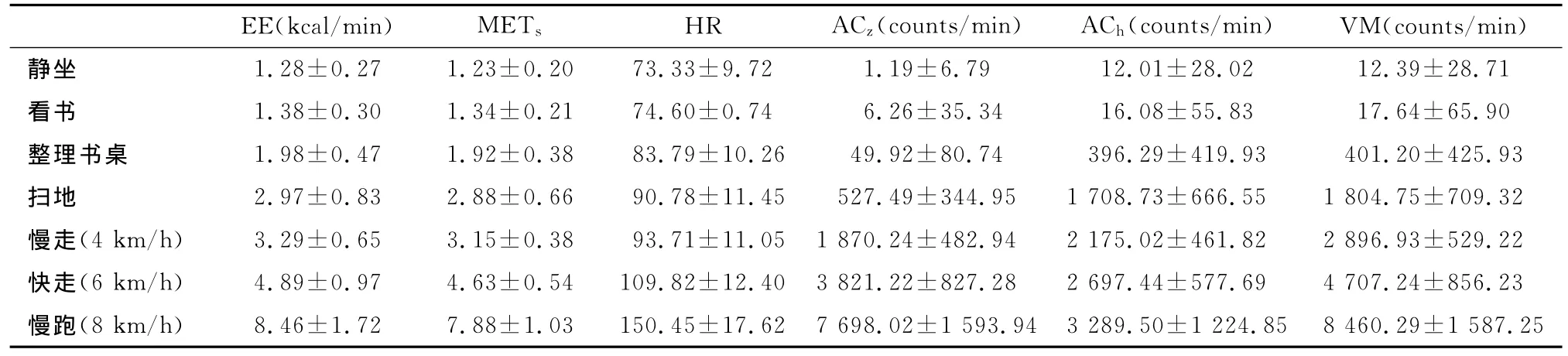
表3 本研究实验组7项体力活动的能耗、心率和加速度计数一览表Table 3 Energy Expenditure，HR and AC of 7Activities of Development Group （D）

EE（kcal／min） METs HR ACz（counts／min） ACh（counts／min） VM（counts／min）静坐 1.28±0.27 1.23±0.20 73.33±9.72 1.19±6.79 12.01±28.02 12.39±28.71看书 1.38±0.30 1.34±0.21 74.60±0.74 6.26±35.34 16.08±55.83 17.64±65.90整理书桌 1.98±0.47 1.92±0.38 83.79±10.26 49.92±80.74 396.29±419.93 401.20±425.93扫地 2.97±0.83 2.88±0.66 90.78±11.45527.49±344.951708.73±666.55 1804.75±709.32慢走（4km／h） 3.29±0.65 3.15±0.38 93.71±11.051870.24±482.942175.02±461.82 2896.93±529.22快走（6km／h） 4.89±0.97 4.63±0.54109.82±12.403821.22±827.282697.44±577.69 4707.24±856.23慢跑（8km／h） 8.46±1.72 7.88±1.03150.45±17.627698.02±1593.943289.50±1224.858460.29±1587.25

从表4可以看出，AC与体力活动能耗的相关性具有高度显著性意义（P＜0.01），但ACh与能耗的相关性受体力活动方式的影响较大，在走／跑类活动中ACh与能耗的相关性较低。VM和ACz都与能耗呈高度相关性，其中，VM与能耗的相关性最稳定，提示，VM为推算能耗的最佳自变量。

在实验组7项体力活动的综合数据中，VM与能耗呈高度正相关关系（P＜0.01），VM与 METs的拟合程度最佳，其判别系数R2为0.92（图1）。

2.2 现有VM能耗方程在实验组7项体力活动能耗监测中的效度

采用S-kcal方程、Actilife联合方程和S-METs方程可推算出实验组7项体力活动的能耗（表5）。可以看出，3个方程都会严重低估非走／跑类活动的能耗（P＜0.01）。在走／跑类活动中，3个方程所推算的快走能耗与IC法测试值均无显著性差异（P＞0.05）。但是，S-kcal方程和Actilife联合方程会显著低估慢走能耗（P＜0.01），略高估慢跑能耗（P＜0.05）。

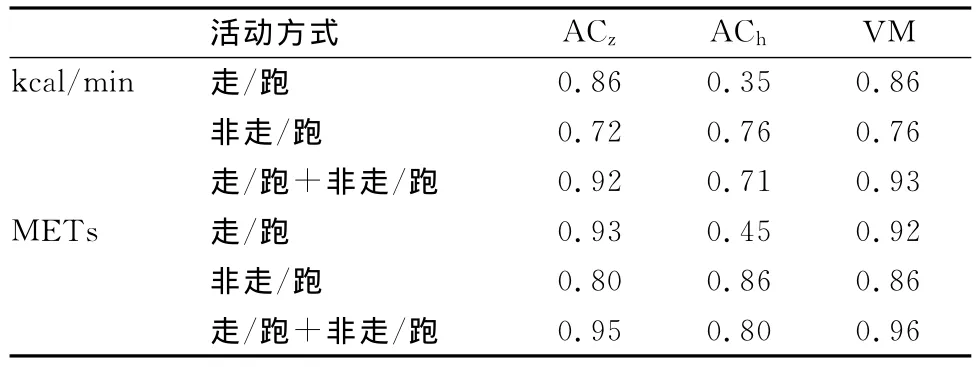
表4 本研究中AC与体力活动能耗的相关性一览表Table 4 Correlation of AC and Energy Expenditure of Physical Activities

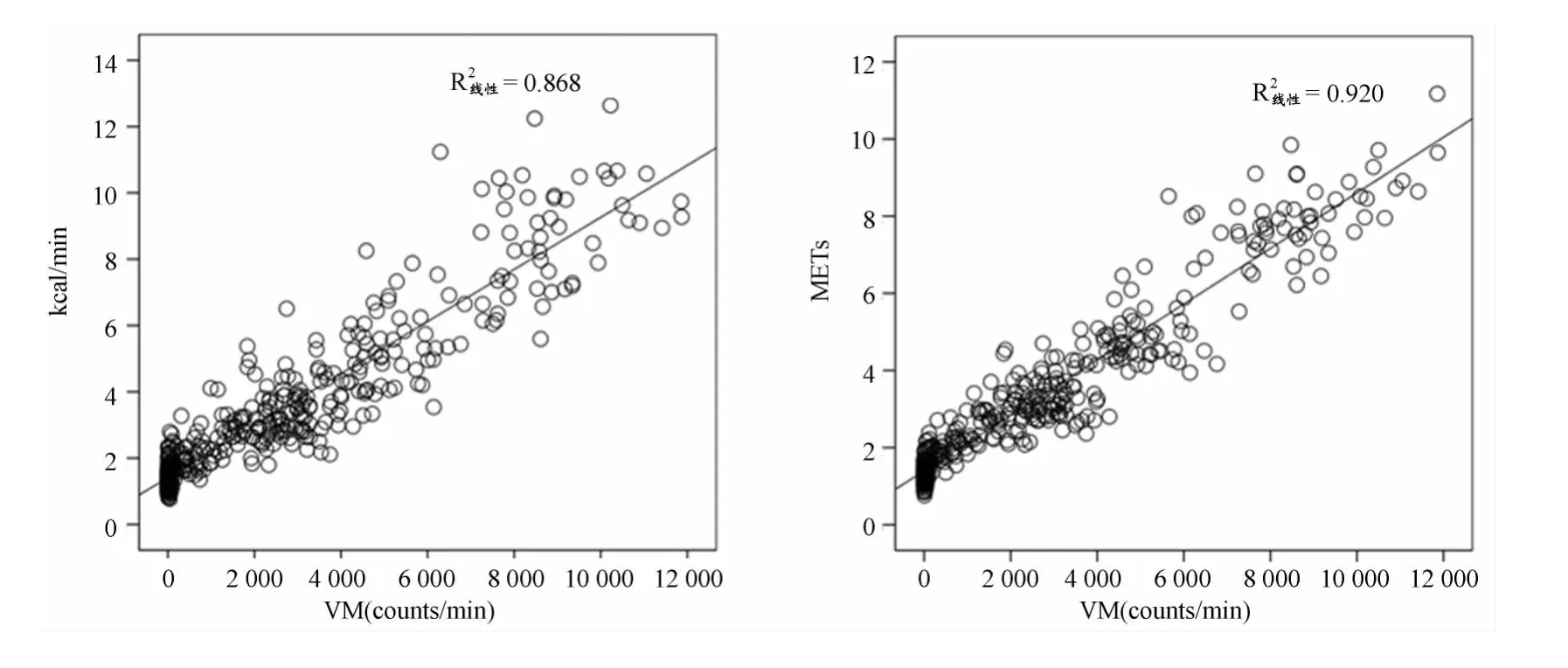
图1 本研究实验组VM与能耗的散点图Figure 1.Scatter Plot for VM Versus Energy Expenditure of Development Group

表5 本研究中IC法和现有方程对7项体力活动的能耗测量值一览表Table 5 Energy Expenditure of 7Activities Measured by IC and Predicted by Equations （D）

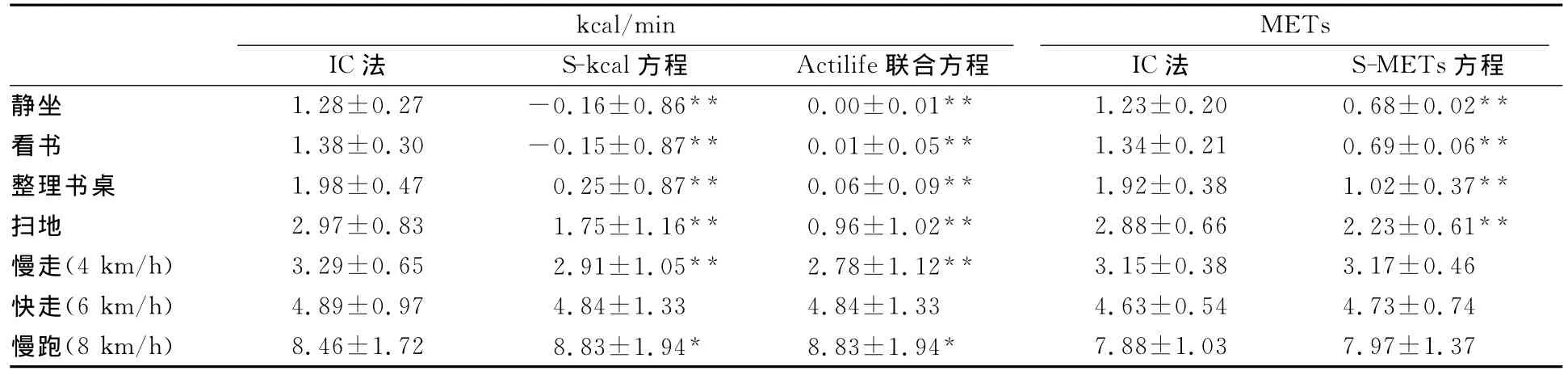
表5 本研究中IC法和现有方程对7项体力活动的能耗测量值一览表Table 5 Energy Expenditure of 7Activities Measured by IC and Predicted by Equations （D）

注:＊表示方程的预测值与IC法实测值的差异具有显著性（P＜0.05）；＊＊表示方程的预测值与IC法实测值的差异具有高度显著性（P＜0.01）。

kcal／min METs IC法 S-kcal方程 Actilife联合方程 IC法 S-METs方程静坐 1.28±0.27 -0.16±0.86＊＊ 0.00±0.01＊＊ 1.23±0.20 0.68±0.02＊＊看书 1.38±0.30 -0.15±0.87＊＊ 0.01±0.05＊＊ 1.34±0.21 0.69±0.06＊＊整理书桌 1.98±0.47 0.25±0.87＊＊ 0.06±0.09＊＊ 1.92±0.38 1.02±0.37＊＊扫地 2.97±0.83 1.75±1.16＊＊ 0.96±1.02＊＊ 2.88±0.66 2.23±0.61＊＊慢走（4km／h） 3.29±0.65 2.91±1.05＊＊ 2.78±1.12＊＊ 3.15±0.38 3.17±0.46快走（6km／h） 4.89±0.97 4.84±1.33 4.84±1.33 4.63±0.54 4.73±0.74慢跑（8km／h） 8.46±1.72 8.83±1.94＊ 8.83±1.94＊7.88±1.03 7.97±1.37

2.3 能耗预测方程的建立

从表4和图1可知，VM与能耗具有良好的线性关系，因此，本研究采用逐步回归法建立体力活动绝对能耗和相对能耗的预测方程（表6）。方程1包括VM和BM两个自变量，方程2以VM为独立自变量。方程1与方程2的判别系数R2都高于0.9，且SEE较低，提示，两个方程的拟合程度都较高（表6）。

表6 本研究所建能耗预测方程一览表Table 6 Energy Expenditure Prediction Equations Developed in this Study

2.4 临界点的建立

根据方程2可推算出3METs和6METs对应的VM临界点，简称为临界点E（Thresholds Derived from Equation2），其数值分别为 2221counts／min 和 6381 counts／min。本研究还采用ROC曲线法建立了另一组VM临界点（简称为临界点R），此组临界点的AUC都高于0.9，且敏感度和特异性都较高（表7）。如图2所示，两根ROC曲线都很接近图的左上角位置，提示，该组临界点具有高度诊断价值。

表7 本研究以ROC曲线法建立的VM临界点一览表Table 7 VM Thresholds Developed by ROC Curve

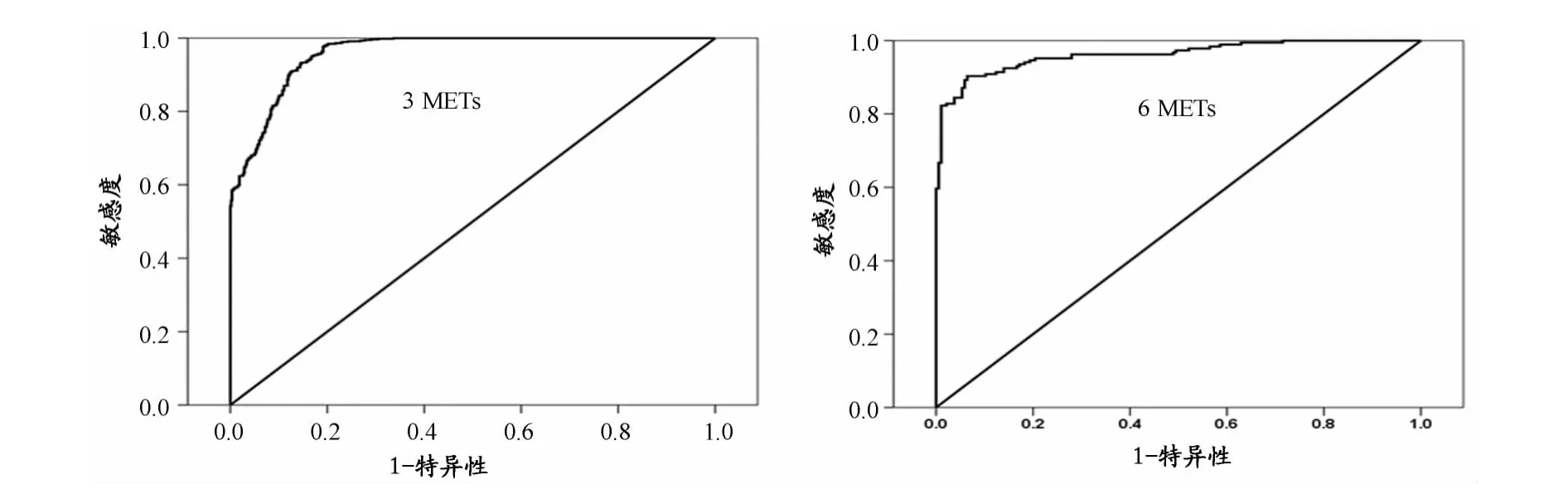
图2 本研究建立VM临界点的ROC曲线图Figure 2.ROC Curve of VM Thresholds

2.5 4h体力活动验证结果

2.5.1 方程监测PAEE4h的准确性

配对t检验显示，S-Kcal方程、Actilife联合方程和SMETs方程的PAEE4h预测值明显低于IC法测试值（P＜0.01），方程1、方程2的PAEE4h预测值与IC法测试值无显著性差异（P＞0.05）；各方程的PAEE4h预测值与IC法测试值均呈现中度相关性（P＜0.01），方程1、方程2的PAEE4h预测值与IC法测试值的相关系数大于其他方程（表8）。如图3所示，方程1、方程2对PAEE4h的能耗预测误差均在95%置信区间之内，其中，方程2的预测误差更为集中。

表8 本研究中IC法和各方程所监测的PAEE4h一览表Table 8 PAEE4hMeasured by IC and Predicted by Equations

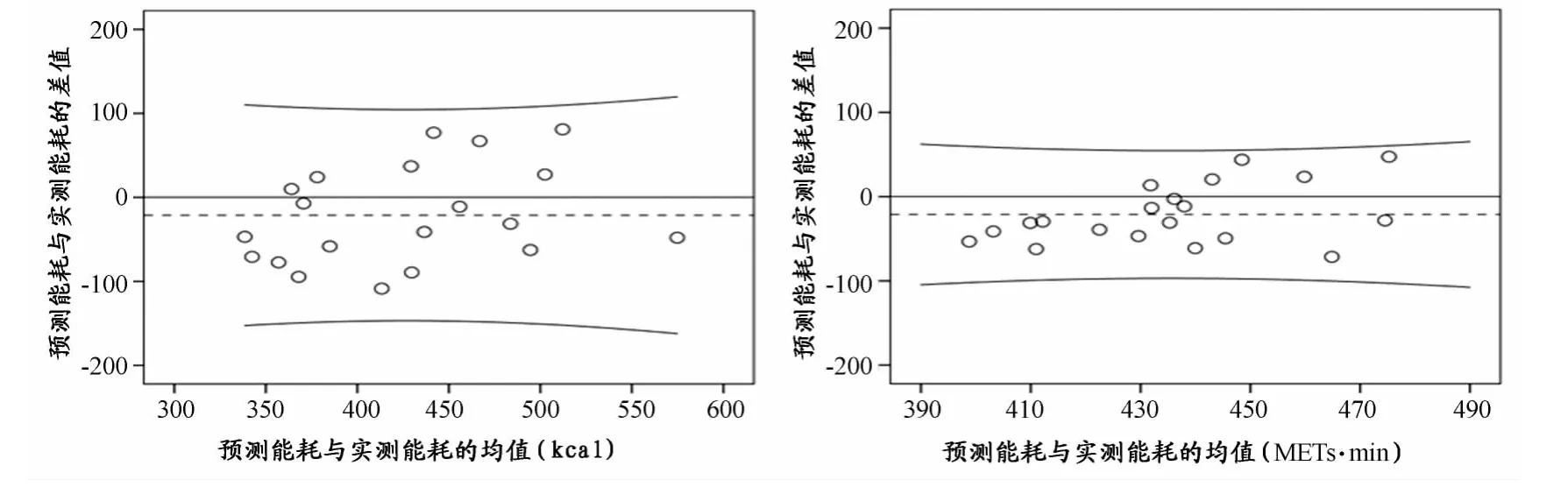
图3 本研究方程1、方程2预测PAEE4h的Bland-Altman散点图Figure 3.The Bland-Altman Plot of PAEE4hPredicted by Equation 1and Equation 2

2.5.2 各组临界点判断低、中、高强度体力活动时间的准确性

如表9所示，临界点S和临界点E测量所得的LPA、MPA、VPA和MVPA时间与IC法测量结果具有显著性差异，临界点S会显著低估MPA和MVPA时间，临界点E会显著高估MPA和MVPA时间。临界点R的测量结果与IC法测试值无显著性差异（P＞0.05）。

表9 本研究中IC法和各组临界点所测得的体力活动时间一览表Table 9 Duration of Physical Activities Measured by IC and VM Thresholds （D）

表9 本研究中IC法和各组临界点所测得的体力活动时间一览表Table 9 Duration of Physical Activities Measured by IC and VM Thresholds （D）

注:＊表示预测值与IC法测试值的差异具有显著性（P＜0.05）；＊＊表示预测值与IC法测试值的差异具有高度显著性（P＜0.01）。

LPA时间 MPA时间 VPA时间 MVPA 时间IC 法 211.70±5.69 20.85±3.86 2.90±1.25 23.75±3.57临界点S 214.80±4.10＊ 18.60±2.58＊ 2.05±1.05＊＊ 20.65±2.98＊＊临界点E 208.35±4.18＊＊ 25.15±2.51＊＊ 1.95±0.83＊＊ 27.10±2.94＊＊临界点R 210.75±3.96 22.15±2.24 2.55±1.15 24.70±2.82

3 分析与讨论

3.1 实验方案分析

Actigraph三轴加速度传感器已逐渐成为体力活动监测中应用最广的加速度传感器之一，其能耗预测方程和AC临界点对其体力活动监测效度至关重要。Actigraph公司官方推荐的能耗预测方程和临界点大都建立在跑台运动实验的基础之上。然而，许多学者［5，13，15，18］都认为，仅以跑台运动的数据所建方程难以准确反映日常体力活动中AC与能耗的关系，要使能耗方程较好地预测日常体力活动的能耗，在建立方程和临界点时有必要采用走／跑与非走／跑类体力活动组合的实验方案。除 Hendelman［13］和Swartz［26］曾采用步行及其他10余种非走／跑类体力活动建立以ACz为自变量的能耗预测方程外，还没有学者采用类似的方案建立以VM为自变量的Actigraph三轴加速度传感器能耗方程。有研究［15］证实，以上两位学者所建方程对长时间体力活动总能耗的预测准确性优于其他方程；但Basset等［7］发现，这两个方程对不同种类体力活动的能耗预测误差波动较大。这既可能与单轴加速度传感器无法监测 ACh有关，也可能是因为 Hendelman［13］和 Swartz［26］的实验中以上肢活动为主的体力活动所占比例过高。

从以上分析可以看出，在建立加速度传感器能耗预测方程时，应充分考虑到被监测人群的体力活动习惯，选择适宜数量和种类的体力活动建立实验方案。因此，本研究在建立能耗预测方程的实验方案中特选用了3种速度的场地走／跑和4种非走／跑活动。其中，看书是有少量肢体活动的坐姿体力活动，整理书桌是以上肢活动为主的站姿体力活动，扫地是上、下肢活动兼具的站姿体力活动。上述活动的肢体活动特点和活动强度在人们的日常体力活动中都具有较强代表性，符合我国青年人日常体力活动习惯。

有研究发现，在极高强度（≥9METs）体力活动（very vigorous physical activity，vVPA）中随着能耗的增加，Actigraph加速度传感器的ACz和VM的增加趋缓，甚至出现平台现象，这可能与Actigraph加速度传感器所设定的采样频率范围等因素有关［8，14，21，22］。考虑到vVPA在日常体力活动中所占比例很低，且AC平台现象会严重影响能耗预测方程和VM临界点的建立，因此，本研究实验方案中未纳入vVPA，也未对9METs所对应的VM临界点进行研究。

3.2 体力活动的能耗和AC特征

从表3可见，实验组的体力活动方案以中、低强度活动为主，与日常生活中的体力活动强度相似。与其他采用跑台运动方案的研究结果相比，本研究中受试者场地走／跑的能耗和心率都较低［1，4］。同等速度下的场地走／跑和跑台运动中人体的肌肉动员模式、步态学、心理状况和地面反应力都有所差别，场地测试时人体运动方式更经济有效，这可能是场地测试时能耗和心率都较低的主要原因［1］。这一差别提示，在加速度传感器能耗预测方程的建立和验证中，采用场地测试的实验方案更符合日常体力活动监测的实际需要。

通过监测实验组7项常见体力活动的AC可见，在快走、慢跑等下肢和躯干位移幅度较大的活动中ACz占据优势，但在整理书桌、扫地等以上肢活动为主的体力活动中ACh高于ACz，这与 Midorikawa等［16］的研究结果相似。从相关性分析可以看出，在走／跑类活动中ACz与能耗的相关性较高，在非走／跑类活动中ACh与能耗的相关性较高，可见，不同类型体力活动中ACz和ACh与能耗的相关关系有较大差异。走／跑类活动中ACh与kcal／min和 METs的相关系数仅为0.35和0.45，提示，ACh不适用于走／跑能耗的监测。VM是将ACz和ACh整合后的变量，尽管在7项体力活动的综合数据中，ACz、VM与能耗的相关系数相似，但在非走／跑类活动中VM与能耗的相关系数较高。从VM与能耗的相关系数和散点图分析可知，VM在不同类型体力活动中始终与能耗保持稳定的高度相关性，提示，VM可全面地反映体力活动中身体的活动情况，在日常体力活动能耗监测中的应用价值高于ACz。

3.3 能耗预测方程的效度分析

3.3.1 已有VM方程对不同类型体力活动的能耗预测效度

根据本研究实验组的数据可知，S-kcal方程会严重低估静坐、看书、整理书桌和扫地的能耗，略低估慢走能耗、高估慢跑能耗，仅能较准确监测快走的能耗，这可能与Sasaki等［22］的实验方法有关。在 Sasaki等［22］的研究中受试者为欧美人，其平均体重为71.6kg，平均BMI为23.8 kg／m2，而本研究中对应的数值分别为60.6kg和21.1 kg／m2，可见，欧美人种与我国青年人群的形体特征存在很大差异。此外，Sasaki等［22］的实验方案中仅包含了4种速度的跑台运动，未纳入其他类型体力活动的数据。以上两方面的原因共同导致S-kcal方程严重低估低强度体力活动能耗，且其误差易受体重的影响。由于S-kcal方程的常量较低（-5.500229），凡是体重低于62.85kg的个体，在VM＝0时以该方程推算出的能耗都为负值。随着VM的提高，该方程受体重的影响逐渐缩小，达到快走时趋于平衡。但是，当达到慢跑强度时，该方程由最初的低估能耗转为高估能耗。由此可推测，由于S-kcal方程中VM的系数较高（0.001064），在高强度体力活动中该方程可能会高估能耗。总体上看，在我国青年人群的体力活动能耗监测中，S-kcal方程会严重低估低强度活动能耗，并呈现高估高强度活动能耗的趋势。

为提高Actigraph三轴加速度传感器对低强度体力活动能耗的预测效度，在Actilife软件内置的VM联合方程中，S-kcal方程仅限于VM＞2453counts／min时使用，当VM≤2453counts／min时则以 W-Kcal方程推算能耗。但是，W-Kcal方程的自变量为ACz，若以该方程推算，只有当ACz达到873counts／min时一名体重60kg受试者的能耗才能达到1kcal／min，而大部分坐姿低强度体力活动的ACz都很低，因此，W-Kcal方程还是会严重低估低强度体力活动的能耗。从表6可见，从静坐、看书过渡到整理书桌和扫地后，ACz数值的增加幅度明显低于VM数值的增加幅度，导致由Actilife联合方程推算出的能耗反而低于由S-kcal方程推算出的能耗。可见，Actilife联合方程并不能有效解决S-kcal方程低估低强度活动能耗的问题。王军利等［4］研究发现，Actilife联合方程虽然会在一定程度上低估跑台运动能耗，但其系统误差较小且较稳定，提示，Actilife联合方程在我国青年人群运动能耗预测中的效度优于S-kcal方程。但是，该研究未进行低强度体力活动，所以，未发现以上方程对低强度体力活动能耗的严重低估。

从表5还可看出，S-METs方程仅能有效预测走／跑类活动的相对能耗。Crouter等［11］研究发现，在以AC为独立自变量的METs预测方程中，截距和斜率是影响方程效度的重要因素。S-METs方程的截距为0.668876METs，在看书、使用电脑等VM较低的坐姿体力活动中，以该方程推算出的体力活动强度约为0.7METs，但其实际强度约为1.2～1.5METs，可见，该方程会严重低估坐姿低强度体力活动的强度。这一现象提示，仅以走／跑为基础建立的能耗预测线性方程在应用于其他类型日常体力活动的能耗监测时其效度会明显降低［9，13，15，18］。

从上述分析可知，S-kcal方程、Actilife联合方程和SMETs方程都无法较好地同步监测我国青年人群的多种日常体力活动能耗，这可能与建立方程时的实验对象、实验方案等因素有关。因此，有必要以我国青年人群为实验对象，以更严谨的实验方案建立适合我国青年人群的体力活动能耗方程。对本研究实验组的数据分析可知，VM在多种体力活动中始终与能耗保持高度相关性，因此，本研究采用经典的逐步回归法建立了以VM（和BM）为自变量的能耗预测方程。

与S-kcal方程相比，方程1的常量较大，但VM和BM的系数较低，从而有效降低了方程对低强度体力活动能耗的预测误差。例如，当VM分别为0和400counts／min时，以方程1推算的60kg个体的体力活动能耗分别为1.29 kcal／min和1.61kcal／min，与本研究所测得的静坐和整理书桌的平均能耗接近。与S-METs方程相比，方程2的截距较高而VM的系数较低，有利于降低方程对低强度体力活动能耗的低估，均衡方程对非／走跑类与走／跑类体力活动的能耗监测误差。

3.3.2 方程对PAEE4h的预测效度

由于IC法可直接测得每分钟的体力活动能耗和一段时间内的体力活动总能耗，在验证方程和临界点的体力活动监测效度时宜采用IC法作为参考标准［11，18，20，24］。考虑到受试者不宜长时间佩戴K4b2，本研究特以受试者实际生活中各体力活动所占时间比例将一周体力活动浓缩到约4h中。尽管验证时间有限，但4h中的体力活动组合与日常体力活动相似，因此，验证结果可较准确地反映各方程和临界点在长时间体力活动能耗监测中的误差水平，Rowlands［20］、Strath［24］等也曾采用类似的方法进行研究。

通过对PAEE4h的验证可见，S-kcal方程、Actilife联合方程和S-METs方程都会严重低估长时间日常体力活动总能耗。如表8所示，S-kcal方程所推算出的部分受试者PAEE4h是负值，这是因为受试者体重轻低且4h的总VM也较低。尽管在同等情况下Actilife联合方程和S-METs方程所推算出的能耗不会出现负值，但这两个方程仍会明显低估PAEE4h。总之，上述方程都会低估PAEE4h，其直接原因主要是这些方程都会明显低估坐姿低强度体力活动的能耗，其间接原因可能是Sasaki等［22］在建立方程时未纳入此类体力活动的数据。

经配对t检验可知，本研究所建方程1、方程2的PAEE4h预测值与IC法测试值呈中度相关关系，两个方程虽然都会略低估PAEE4h，但其误差均不具备统计学意义（P＞0.05）。以Bland-Altman图分析可知，两个方程对验证组受试者PAEE4h的预测误差都位于95%置信区间之内，提示，其预测准确性都较高。可见，本研究所建能耗方程可更准确地预测日常体力活动能耗，这可能是由于本研究的实验方案中兼顾到了安静状态、低强度和中高强度体力活动，同时也兼顾到了坐姿、站姿和行进间等多种身体姿态。

本研究所建方程略低估PAEE4h，在很大程度上可能是因为低估了自行车和上楼梯等活动的能耗。无论是单轴还是三轴加速度传感器，其佩戴位置均为腰部，因此，无法准确感应骑车时的下肢活动，还会低估抗阻运动、负重运动等特殊活动的能耗［11，17，27］。 刘爱玲等［2］曾预先记 录 骑车的时间、速度和距离，再对加速度传感器所推算出的总能耗进行校正，以提高加速度传感器的能耗监测效度，该方法可在今后的研究中加以借鉴。方程1和方程2略低估PAEE4h还可能是因为在vVPA中AC易出现平台现象，导致方程低估此类活动的能耗［8，11，14，22］。 今后可专门针对vVPA开展Actigraph三轴加速度传感器的能耗监测研究，为提高其体力活动监测效度提供更多依据。

还需注意的是，尽管方程1整体误差较低，但从Bland-Altman散点图分析可知，该方程预测PAEE4h时误差较分散，提示，方程1对个体的预测误差存在较大的变异性，这可能是因为受试者体重会影响到方程所推算出的绝对能耗。与之相比，相对能耗单位（如METs）排除了体重对能耗的影响，更侧重于对活动强度的评估。而且，METs和kcal／min之间可通过“kcal／min＝MET×3.5×体重（kg）／200”方程相互转换［23］。因此，有学者在加速度传感器能耗预测研究中以 METs作为能耗单位［11，17］。从Bland-Altman散点图分析可见，方程2对PAEE4h的预测误差较集中。因此，本研究建议在日常体力活动能耗监测中优先选用以METs为单位的方程。

3.4 VM临界点的效度分析

2008年出版的《美国体力活动指南》［19］建议成人每周MVPA时间不低于150min，加速度传感器的一个重要功能正是依靠AC临界点监测各强度体力活动的时间。然而，Actilife软件中至今仍主要以Freedson等［12］在1998年所建的ACz临界点判断各强度体力活动的时间，对VM临界点的研究和应用都较少。在以往的研究中，学者们大都先以METs为因变量建立直线回归方程，再推导出3 METs和6METs所对应的AC临界点。近年来，一些学者开始采用ROC曲线法建立AC临界点［5，17］。为了确定最佳的VM临界点，本研究采用上述两种方法各建立了一组VM临界点，并以IC法为标准验证了临界点S及本研究所建临界点在4h日常体力活动监测中的准确性。

验证结果显示，临界点S会显著高估LPA时间，显著低估MPA时间、VPA时间和 MVPA时间，提示，临界点S的数值偏高。临界点E则会显著高估MPA和MVPA时间，显著低估LPA和VPA时间。以上两组VM临界点都是由以METs为因变量的直线回归方程推导得来，尽管这种方法简便易行，但是，以该方法建立的临界点无法准确地平衡临界点附近的监测误差，易导致临界点在某一方向的误判率偏高［27］。相反，以ROC曲线法建立的临界点R可较好地监测4h内各强度体力活动的时间，提示，ROC曲线法是建立AC临界点的一个有效方法。

ROC曲线法可计算多个临界点的敏感度和特异性，从而筛选出敏感度和特异性都较高的临界点。敏感度是指阳性受检者中被查出阳性者所占百分比，特异性是指阴性受检者中被查出阴性者所占百分比。在ROC曲线法中，变量的诊断价值主要依靠AUC来判断，AUC在0.5～0.69之间时诊断价值较低，在0.7～0.89之间时诊断价值中等，达到0.9则诊断价值较高［3］。本研究显示，以ROC曲线法建立VM临界点时，两个临界点的AUC都大于0.9，临界点的敏感度和特异性也较高，提示，VM可作为区分体力活动强度的有效指标。

以ROC曲线法建立临界点时，研究人员可以根据不同的诊断目的来确定最佳临界点，主要方法有:1）为便于早期筛查，降低漏诊比例，可选择敏感度高的临界点；2）要确保疾病诊断的准确性，降低误诊比例，可以选择特异性较高的临界点；3）如果漏诊和误诊同等重要，可选择将“敏感度＝特异性”的点作为临界点，也可选择Youden指数（敏感度＋特异性-1）最高的点作为临界点［3］。

由于建立VM临界点的目的是为了准确分析LPA时间、MPA时间和VPA时间，均衡VM临界点对临界强度上下数据的“漏诊”和“误诊”幅度成为确定最佳临界点的关键。为此，本研究在进行ROC曲线分析时，特在低于和高于临界强度的数据中选取等量数据进行分析，并采用“敏感度＝特异性”的方法来确定VM临界点。经验证，临界点R可较准确地分析不同强度的体力活动时间，其诊断能力达到了预期水平。

4 结论

本研究显示Actigraph三轴加速度传感器所测VM是监测体力活动的有效变量，但S-kcal方程、S-METs方程、Actilife联合方程以及切点S都不适合我国青年日常体力活动监测。本研究在多种日常体力活动基础上建立的能耗预测方程和采用ROC曲线法建立的临界点具有较高的效度，适用于我国青年人群日常体力活动监测。今后还可扩大研究对象的年龄范围，并增加对vVPA和骑车等特殊活动的针对性研究。

［1］江崇民，邱淑敏，王欢，等.平板运动跑台和场地环境测试走、跑运动能量消耗的比较研究［J］.体育科学，2011，31（7）:30-35.

［2］刘爱玲，李艳平，宋军，等.加速度计对成人日常体力活动测量效度的研究［J］.中华流行病学杂志，2005，26（3）:197-200.

［3］王建华.流行病学［M］.北京:人民卫生出版社，2008:87-92.

［4］王军利，张冰，贾丽雅，等.Actigraph（GT3X）加速度计测量我国19～29岁人群身体活动能耗的效度研究［J］.体育科学，2012，32（12）:71-77.

［5］朱琳，陈佩杰.应用ROC曲线确定活动计数在青春期少年运动强度诊断中的最佳临界值［J］.体育科学，2012，32（11）:70-75.

［6］Actilife software data scoring［EB／OL］.https:／／help.theactigraph.com／entries／ 20744123-What-is-the-difference-amongthe-Energy-Expenditure-Algorithms.

［7］BASSET D R J R，AINSWORTH B E，SWARTZ A M，et al.Validity of four motion sensors in measuring moderate intensity physical activity［J］.Med Sci Sports Exe，2000，32（9）:S471-480.

［8］BRAGE S，WEDDERKOPP N，FRANKS P W，et al.Re-examination of validity and reliability of the CSA monitor in walking and running［J］.Med Sci Sports Exe，2003，35（8）:1447-1454.

［9］CHARLES E M.Calibration of accelerometer output in adults［J］.Med Sci Sports Exe，2005，37（11）:S512-522.

［10］CHEN K Y，SUN M.Improving energy expenditure estimation by using a triaxial accelerometer［J］.J Appl Physiol，1997，83（6）:2112-222.

［11］CROUTER S E，CHURILLA J R，BASSETT D R J R.Estimating energy expenditure using accelerometers［J］.Euro J Appl Physiol，2006，98（6）:601-612.

［12］FREEDSON P S，MELANSON E，SIRARD J，et al.Calibration of the Computer Science and Applications，Inc.accelerometer［J］.Med Sci Sports Exe，1998，30（5）:777-781.

［13］HENDELMAN D，MILLER K，BAGGETT C，et al.Validity of accelerometry for the assessment of moderate intensity physical activity in the field［J］.Med Sci Sports Exe，2000，32（9）:S442-449.

［14］KING G A，TORRES N，POTTER C，et al.Comparison of activity monitors to estimate energy cost of treadmill exercise［J］.Med Sci Sports Exe，2004，36（7）:1244-1251.

［15］LEENDERS N Y，SHERMAN W M，NAGARAJA H N.Energy expenditure estimated by accelerometry and doubly labeled water:do they agree［J］.Med Sci Sports Exe，2006，38（12）:2165-2172.

［16］MIDORIKAWA T，SHIGEHO T，KAYOKO K，et al.Evaluation of low-intensity physical activity by triaxial accelerometry［J］.Obes，2007，15（12）:3031-3037.

［17］NANCY F B，ULF E，KLAAS R W.Assessing physical activity using wearable monitors:measures of physical activity［J］.Med Sci Sports Exe，2012，44（S1）:S5-12.

［18］PATTY F，HEATHER R B，RICHARD T，et al.Assessment of physical activity using wearable monitors:recommendations for monitor calibration and use in the field［J］.Med Sci Sports Exe，2012，44（S1）:S1-4.

［19］PHYSICAL ACTIVITY GUIDELINES ADVISORY COMMITTEE.Physical activity guidelines advisory committee report［M］.Washington DC:U.S.Dept Health Human Services，2008:A6-A8.

［20］ROWLANDS A V，POWELL S M，HUMPHRIES R，et al.The effect of accelerometer epoch on physical activity output measures［J］.J Exe Sci Fit，2006，4（1）:52-58.

［21］ROWLANDS A V，STONE M R，ESTON R G.Influence of speed and step frequency during walking and running on motion sensor output［J］.Med Sci Sports Exe，2007，39（4）:716-727.

［22］SASAKI J E，JOHN D，FREEDSON P S.Validation and comparison of ActiGraph activity monitors［J］.J Sci Med Sport，2011，14（5）:411-416.

［23］SCHNEIDER P，Kaminsky L.Tips for Helping Clients Meet Energy Expenditure Goals［J］.ACSM＇S Health Fit J，2006，10（3）:15-21.

［24］STRATH S J，BASSETT JR D R，SWARTZ A M.Comparison of MTI accelerometer cut-points for predicting time spent in physical activity［J］.Int J Sports Med，2003，24:298-303.

［25］STRATH S J，BASSETT JR D R，SWARTZ A M，et al.Simultaneous heart rate-motion sensor technique to estimate energy expenditure［J］.Med Sci Sports Exe，2001，33（12）:2118-2123.

［26］SWARTZ A M，STRATH S J，BASSETT D R，et al.Estimation of energy expenditure using CSA accelerometers at hip and wrist sites［J］.Med Sci Sports Exe，2000，32（9）:S450-456.

［27］WELK G J.Principles of design and analyses for the calibration of accelerometry-based ativity monitors［J］.Med Sci Sports Exe，2005，37（11）:S501-511.