基于ANSYS/LS-DYNA的行星轮系传动系统瞬态动力学分析

陈岚赖诚唐俊

(四川工程职业技术学院，四川 德阳 618000)

0 引言

行星轮系相较于其它传动，具有大速比、效率高、结构紧凑、重量轻及较低的轴承载荷等特点，在重型机械、航天航空机械、汽车等个领域都有广泛的应用。但是由于行星齿轮传动是过约束传动，且结构复杂，所以行星轮系的瞬态动力分析较普通的定轴轮系更为复杂，而其广泛的工程应用要求我们能更快速、便捷地对行星轮系进行各项动态分析。利用ANSYS/LSDYNA/LS通用显式动力学分析软件可以方便快捷地模拟齿轮系统各种动态特性，如非线性应力分布及动力冲击问题，与实验的无数次对比验证了其计算的可靠性。

1 有限元模型的建立

因为整个行星轮系的结构比较复杂，在ANSYS/LS-DYNA中直接建模是比较麻烦的，但是采用UG、Pro/E、CAD等建立的模型，需要转换成IGES格式后导入ANSYS/LS-DYNA，普遍存在一些实体、曲面（曲线）修补或数据丢失的问题，影响计算精度。本文利用ANSYS/LS-DYNA中的APDL参数化语言对轮系进行建模，对整个模型的建立和后期的有限元分析提供了极大的便利。为了使各级齿轮承载较为均匀，行星齿轮和行星架采用悬浮结构。

NGW行星机构参数化建模步骤：

（1）建立局部坐标系；在ANSYS/LS-DYNA软件中，行星齿轮的旋转坐标默认是围绕系统全局坐标系，为了定义行星齿轮轮系中各个齿轮的旋转，故需要定义局部坐标系。

（2）根据渐开线参数方程，在ANSYS/LS-DYNA中产生齿廓曲线（渐开线和圆弧过渡曲线，渐开线的极坐标方程见公式1，齿轮的各项参数见表1），太阳轮齿廓曲线渐开线上点（ri，αi）的极坐标值。

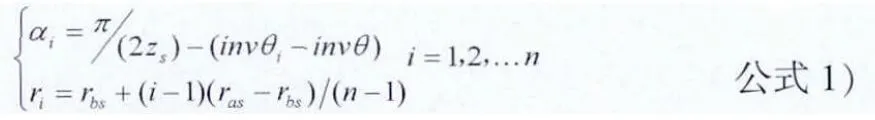
Rbs-----太阳轮基圆半径

Ras------太阳轮齿顶圆半径

n-------渐开线划分的段数，n越大轮齿部分的网格越密，齿轮模型精度越高，计算精度越高，计算效率越低。

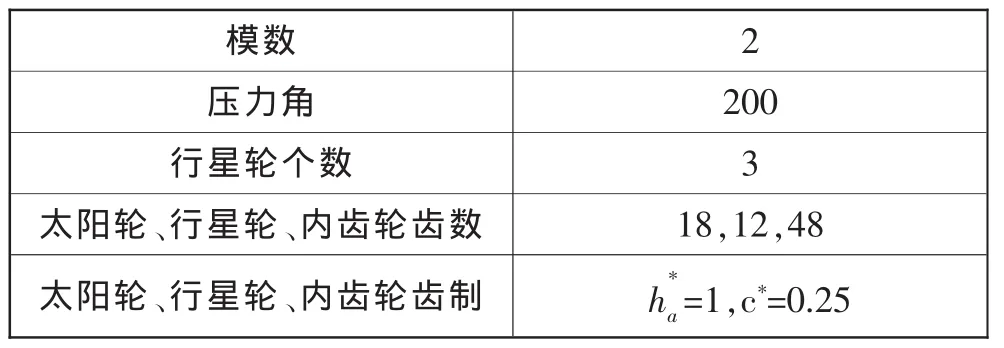
表1 行星轮系基本参数

（3）设置网格形式和划分方式，对齿轮的二维模型进行网格划分[8]；为提高有限元分析的计算精度，在LS—DYNA环境下对行星齿轮模型采用结构化网格进行单元划分，并把模型划分为接触区域和非接触区域两部分．接触区域定义为弹性体，并对接触面的有限元网格进行局部细化为了得到更为精确的数值和加速求解的收敛，对行星齿轮中的各个齿轮的接触部分细化网格，设置材料属性，材料属性见表2。

表2 行星轮系材料属性

（4）依样建立行星轮，最后完成整个行星轮系的有限元模型建立，见图1。

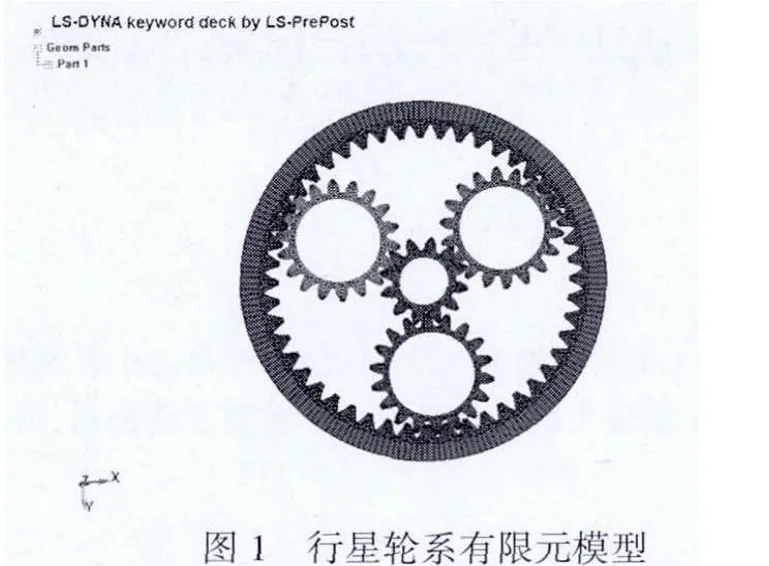
（5）边界条件：约束太阳轮表面节点的径向和轴向位移，只保留轴向的转动自由度．约束行星架的轴向位移，保留轴向转动自由度．约束行星轮轴向位移，行星轮除绕轴向公转外，还可以绕自身轴线自传，齿圈加固定约束．并设定外圈为刚体，采用实体solid164单元；设置齿轮间粘性阻尼，控制齿轮沙漏能，齿轮间的接触为自动的面与面的接触，每个齿的两面都定义接触．通过定义接触对可以保证轮齿啮合时接触部分的受力和变形能够被随时跟踪、定位[8]．求解时间为0.2秒。

2 计算结果

瞬态动力学分析是确定结构在静载荷、瞬态载荷和简谐载荷的随意组合下的随时间变化的力、应力、应变等。求解完成后轮系中各构件所受到的应力分布云图及能量变化曲线图见图 2、图 3、图 4。

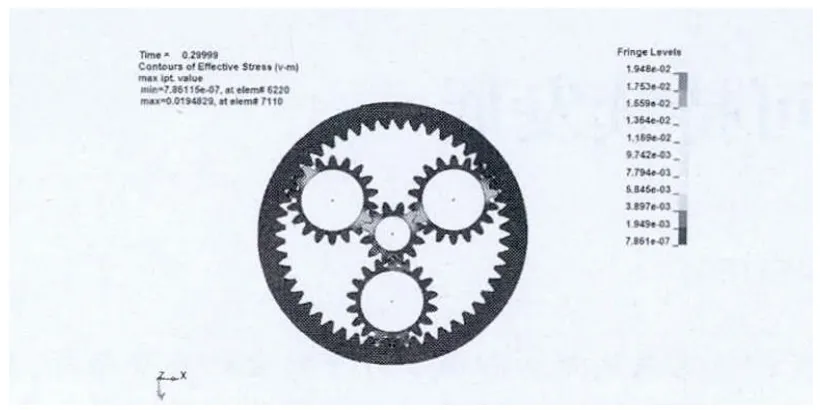
图2 等效应力分布图

图3 最大剪切应力图

计算结果分析：

（1）齿轮的失效主要发生在轮齿表面和轮齿根部，从行星轮系的等效应力分布图上可以看到，工作中，行星齿轮与太阳轮所受最大等效应力基本相等,应力比较大的地方主要集中在啮合轮齿接触处和齿根附近，而且应力影响区只在接触齿对两、三个齿附近，远离接触区域处，应力为零，符合弹性力学中的圣维南定律。

（2）齿轮的最大应力分布在啮合轮齿的齿廓曲面及轮齿根部，随着齿轮的旋转，轮齿的最大应力周期性变化。

（3）最大剪切应力为6.050MPa，最大等效应力为9.742MPa，都小于齿轮的许用应力；应力分布也较为均匀，在齿廓表面和齿根处未出现较明显的应力集中现象。

3 结语

（1）通过显式动力学软件ANSYS/LS-DYNA的强大分析功能，方便快捷地利用静力学仿真数据对行星轮系施加动态载荷，进行动态动力学仿真，得到动态载荷下轮系上个齿轮的应力分布云图和能量变化曲线图，从而判断各零件的强度是否合格，结构是否合理。

（2）ANSYS/LS-DYNA所得数据是传统的分析方法不易得到的，在复杂的机械设计中，有限元的应用为方便快速的解决问题提供了途径，从而为机构的优化设计提供依据。

[1]方宗德，沈允文，黄镇东.2K-H行星减速器的动态特性[J].西北工业大学学报，1990，（8）：361-371

[2]周长城，胡仁喜，熊文波.ANSYS/LS-DYNA11.0基础与典型范例[M].北京：电子工业出版社，2007

[3]丁飞，张强.基于ANSYS/LS-DYNA的行星齿轮减速器的建模与仿真研究[J].煤炭工程，2009（6）：84-86

[4]李黎明.ANSYS/LS-DYNA有限元分析实用教程[M].北京：清华大学出版社，2005

[5]王国强.实用工程数值模拟技术及其在ANSYS/LSDYNA上的实践[M].西安：西北工业大学出版社，1999

[6]HIDAKA,YOSHIOETAL.Analysia of dynamic tooth load on planctary gear[J].Bull JSME,1980，23(17)：315-323