基于Rogowski线圈的数字积分器的研究与设计
王晓明,周有庆,彭红海,张云飞,胡海波
(湖南大学 电气与信息工程学院,湖南 长沙 410082)
0 引言
电子式互感器是实现智能变电站运行实时信息数字化的主要设备,在电网动态观测、提高继电保护可靠性等方面具有重要的作用。近年来,采用Rogowski线圈的电子式电流互感器成为了国内外研究的热点,并且已经进入了实用化阶段。与传统的互感器相比,Rogowski线圈具有低功率输出、动态范围大、不存在磁饱和问题、测量频带宽、经济性好等优点[1-5]。
1 新型PCB平面Rogowski线圈
文献[6]提出了一种新型PCB平面Rogowski线圈结构,该新型PCB平面线圈可以制作成单层或多层来调节所需要的互感系数等参数。以双层板为例,其结构原理图可参见图1。
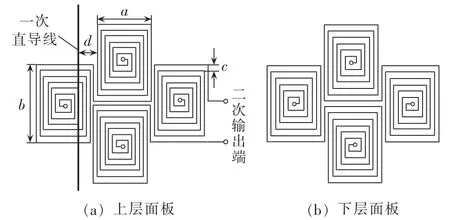
图1 新型PCB平面Rogowski线圈结构Fig.1 Structure of new-style PCB planar Rogowski coil
图1(a)为二次线圈上层示意图,图 1(b)为二次线圈下层示意图。双层PCB板上、下2层均有4个相同的均匀对称分布的平面螺旋线圈,上、下2层螺旋线圈绕向相反,每层相邻的线圈顺次串联,上、下2层之间对应的螺旋线圈通过“过孔”顺次串联,首末两端作为输出端,构成二次输出端。
根据法拉第定律和安培环路定律可知,线圈的二次输出电压 e(t)和被测电流 i(t)之间的关系为:

其中,M为互感系数,计算方法可参见文献[6]。
通过对二次输出电压积分可还原被测信号:
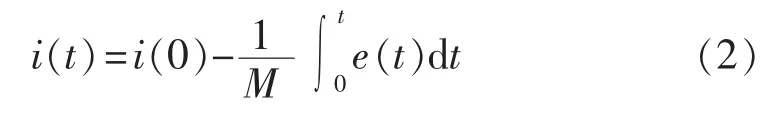
实验表明,该新型Rogowski线圈具有良好的线性度和准确度;式(2)表明高精度的积分环节是确保新型电流互感器精度的关键[7-8]。
2 模拟积分器
常用的模拟积分电路如图2所示,图中Rf能够抑制积分器的直流漂移,为减小其对积分效果的影响,Rf一般取值较大。
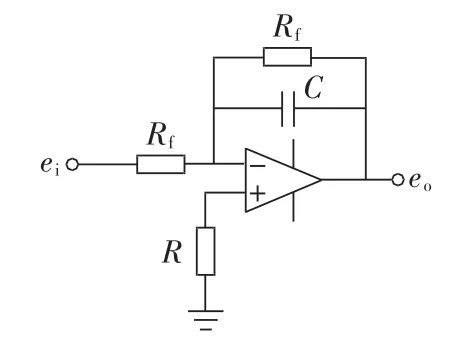
图2 模拟积分电路Fig.2 Circuit diagram of analog integrator
图2所示电路的传递函数为:

其中,R=51 kΩ,C=0.047 μF,Rf=1 MΩ。
通过实验发现,使用该积分器的互感器测试结果误差较大,主要是因为温度对电路中模拟器件的影响[9],由式(3)可得输出电压的值为:
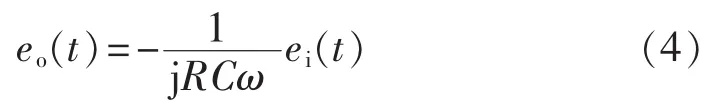
则由温度引起的输出电压误差以及相对误差为:
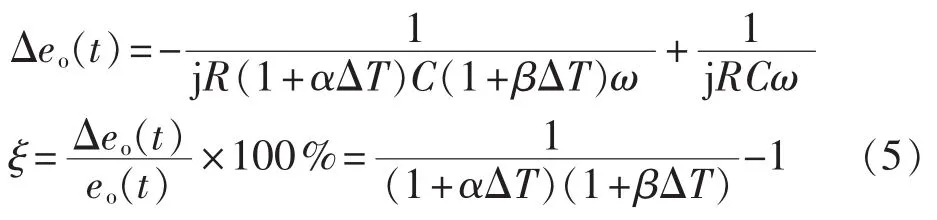
其中,α、β分别为电阻和电容的温度系数,ΔT为温度变化量。
取 α=1×10-5/℃,β=3×10-5/℃,作相对误差曲线图如图3所示。
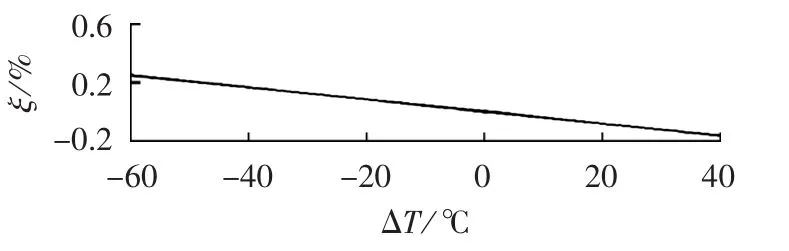
图3 相对误差曲线Fig.3 Curve of relative error
从图3中可以看出,当温度变化较大时,相对误差较大,不满足IEC60044-8标准0.2级的精度要求。
3 数字积分器的设计
3.1 数字积分算法的研究
同模拟积分相比,数字积分具有很多显著的优点。
a.性能稳定。模拟积分器中的模拟器件受温漂和时漂影响,参数会发生变化,导致性能不稳定;数字积分器中的模数转换器和运放驱动电路等模拟电路结构简单稳定,受温漂和时漂影响小,实现其积分器功能的算法完全不受环境因素的影响。
b.相位特性优良。模拟积分器中的模拟器件参数不同,会引入轻微的相位变动,需要进行相位校准;数字积分的相位响应主要由算法决定,具有一致性。
c.数字积分器结构灵活,调节方便[10]。
数字积分器最常用的一种方法是采用模数转换器(ADC)和微处理器芯片(MCU),再设计相应的积分算法来实现。数字积分器框图如图4所示,为了消除直流偏置的影响,在ADC输出与积分器间接入一个数字高通滤波器(HPF)。

图4 数字积分器框图Fig.4 Block diagram of digital integrator
因此选择合适的积分算法成为数字积分器设计的关键问题之一。常用算法有复化的矩形公式、梯形公式和Simpson公式。由文献[11]可知,在相同的精度要求下,矩形公式要求每个周期内的采样点数较多,梯形公式次之,Simpson公式最少,但从算法结构上看矩形公式最简单,梯形公式次之,Simpson公式最为复杂。因此,综合考虑3种算法的优劣,本文设计的积分器采用复化梯形积分算法。
根据数值积分的原理,一般梯形公式为:
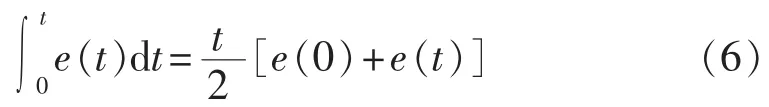
为了提高积分精度,将积分区间[0,t]n等分,步长h=t/n,则可得复化梯形积分公式为:
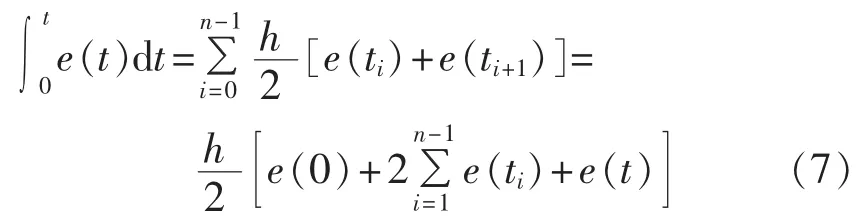
式(7)的z传递函数为:

其中,T为采样间隔。
因为 z=ejω,可得:
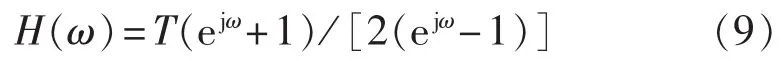
其中,ω=2πf/fs为数字角频率,fs为采样频率。
取 fs=4 kHz,经过仿真可得到如图5所示的频率特性,由图可见,其幅频响应具有-20 dB/(°)的衰减,相频响应具有-90°的相移,与理想积分一致。
3.2 梯形算法对稳态和暂态特性的响应仿真分析
3.2.1 稳态性能分析
电力系统在正常运行时,IEC60044-8标准规定其稳态一次电流为:
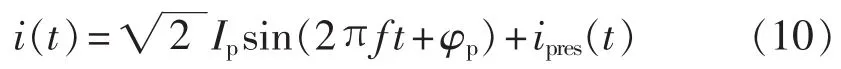
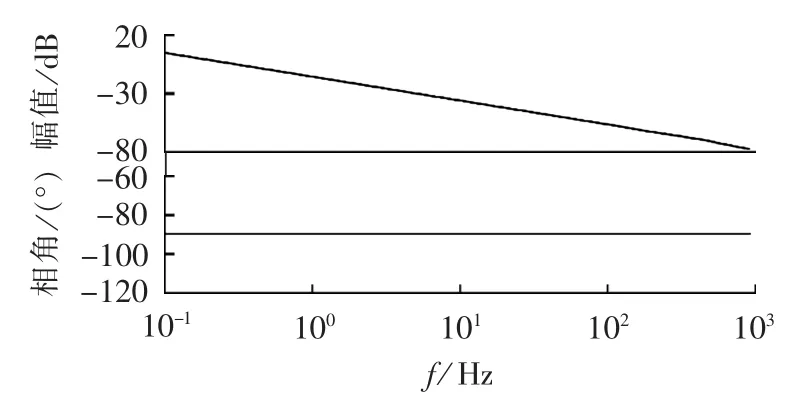
图5 梯形积分的幅频响应Fig.5 Amplitude-frequency response of trapezoidal integrator
其中,Ip为一次电流基波的方均根值;f为基波频率;渍p为一次相位移;ipres(t)为一次剩余电流,包括谐波和分数谐波分量。
取 Ip=0.707,渍p=0,ipres(t)=0.1sin(4πft),由式(1)可得:
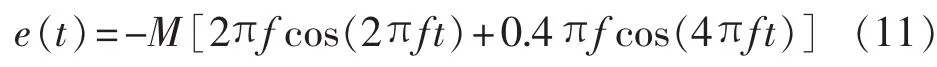
由式(7)可得满足梯形公式的离散方程为:
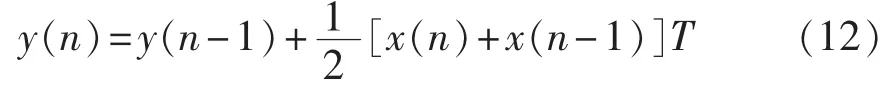
用MATLAB对式(11)进行4kHz的采样,实际中互感系数M数值较小,为方便比较,仿真时令M=1。利用式(12)进行积分运算,可以得到一次输入电流和二次输出电压(已经过数字积分,后同)的图形如图6所示,从图中可以看出,用梯形积分算法可以很好地还原稳态电流。

图6 梯形积分对稳态电流的响应图Fig.6 Response of trapezoidal integrator to steady current
3.2.2 暂态性能分析
电力系统发生故障时,一次故障电流通常包含基频分量、直流分量及高频分量,对暂态电流的响应可视为对各部分分量响应的叠加,IEC60044-8标准规定暂态电流用下式来表示:
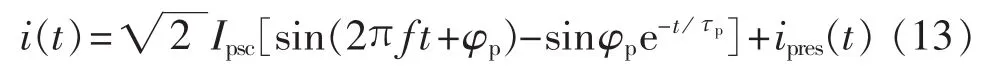
其中,Ipsc为一次电流对称分量方均根值;f为频率;τp为暂态一次时间常数;ipres(t)为一次剩余电流,包括谐波和分数谐波分量。
考虑最严重情况,假定暂态电流为全偏移,则式(13)变为:
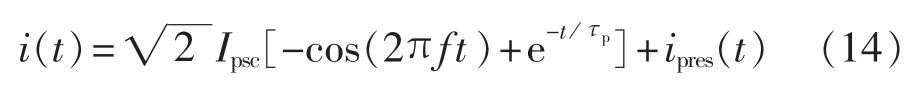
取 Ip=0.707,ipres(t)=0.1sin(4πft),由式(1)可得:

同理,利用MATLAB进行仿真,可得到一次输入电流与二次输出电压的图形如图7所示,从图中可以看出,暂态一次时间常数取不同值时,梯形积分都能很好地还原故障电流。

图7 梯形积分对暂态电流的响应图Fig.7 Response of trapezoidal integrator to transient current
由以上分析可知,采用梯形积分算法能够很好地还原一次电流。
3.3 系统框图
本文设计的新型PCB平面Rogowski线圈结合数字积分的系统框图如图8所示。

图8 系统框图Fig.8 Block diagram of system
该系统采用STM32F103作为核心处理器,该处理器具有运算速度快、工作范围宽、可靠性高、集成AD转换、多个通信接口等特点。如图8所示,PCB平面Rogowski线圈输出的电压信号e(t)先经模拟信号调整电路,其作用主要是滤除信号中的高频干扰信号,并对信号进行差分放大;然后将信号输入到核心处理器中,进行AD转换,运用复化梯形积分算法进行积分运算;再将数字信号传到数模转换器DAC8564中,变为模拟信号,经过后置处理电路的平滑输出e′(t),将 PCB 平面 Rogowski线圈电流互感器输出的电压信号还原成一次电流信号。
3.4 关键问题的设计
a.对于ADC自身或其前置调整电路引起的直流漂移,本文主要通过在ADC输出与数字积分之间接高通滤波器(HPF)来消除直流偏置的影响。
b.积分初值问题。要完全还原被测电流信号,必须确定积分的初值,而ADC采样的初值难以从0开始,这样就会使积分输出产生直流分量。取初相角为 30°,利用式(10)、(11)、(12)进行仿真,一次输入电流与二次输出电压如图9所示,从图中可以看出,积分输出会产生直流分量。
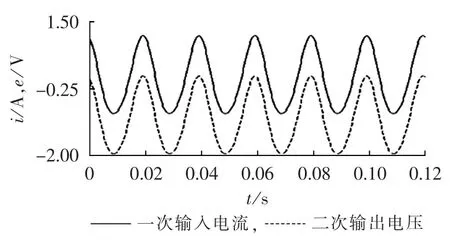
图9 直流分量对积分器的影响Fig.9 Influence of direct current on integrator
为了消除直流分量的影响,可对一定周期内的积分结果取平均值,此平均值则为其直流分量,由式(12)得出直流分量可用式(16)来计算:

其中,N为采样点数。
然后对其积分结果进行补偿,即可消除其直流分量的影响。补偿后的结果如图10所示,从图中可以看出,经过补偿可以消除直流分量的影响,二次电压能够很好地还原一次电流。
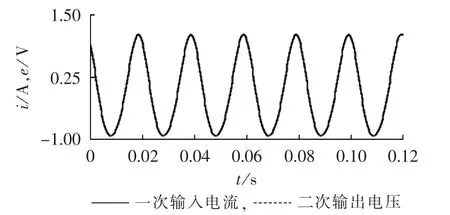
图10 补偿后积分器的输出Fig.10 Output of integrator after compensation
4 实验测试
利用图8所示的系统对其数字积分进行稳态特性测试,在实验室取额定电流为300 A,用全功能互感器校验仪进行比对,得到误差曲线如图11所示。一次与二次波形跟随如图12所示,其中,一次电流已转换成同相位的电压信号。从图11的误差曲线可以看出,采用本文设计的数字积分器的PCB平面Rogowski线圈电流互感器具有很好的线性度,比差和角差误差较小,能够满足电流互感器0.2级的精度要求。由图12的波形图可以看出,其具有很好的稳态特性。由于实验室条件所限,未能对其暂态特性进行实验验证。

图11 实验数据Fig.11 Experimental data

图12 一次电流与二次电压波形图Fig.12 Waveforms of primary current and secondary voltage
5 结论
本文对基于Rogowski线圈的电流互感器的积分技术进行了研究,针对模拟积分受环境影响大的不足,着重对数字积分进行研究并且设计了基于STM32F103和梯形积分算法的数字积分器,实验测试取得令人满意的结果。

