基于无线传感器网络目标定位算法研究

王栋

（西安翻译学院 陕西 710105）

0 前言

目前在无线网络传感器研究领域中，目标定位和跟踪系统是主要的研究对象，也是当前研究的热点内容。目标定位主要是对某一时刻的无线传感器中监测的对象能够进行空间定位，目前在研究过程中主要对声信号进行测量并确定目标定位。其中声目标定位主要分为三种，一种是时差定位，一种是波达方向定位，另一种是接受到的能量定位。时差定位主要是通过传感器的节点接受信号，然后根据接受到的信号进行估计定位。波达方向定位主要是根据传感器节点接受信号时到达方位角的不同，然后根据信号估计定位。能量定位主要依据的是大量的计算和通信方式来实现定位，但是一般不适合用于低功耗的无线传感器网络，因此本文主要探讨的是传感器测量到的声信号目标定位的实现。

1 基于能量的目标定位方法

目前随着社会科学技术的不断发展，无线传感器目标定位主要是基于声音能量信号的估计定位，一般最近点的就是定位计算法。声音能量目标定位算法是将无线传感器中得到的声目标读数为最大值，并将这个最大值作为目标源的位置。声音能量目标定位算法研究中一般只会用到一个节点的信息，往往会存在着较大的误差，不过极大似然定位方法能够实现其高精度的定位，但是参数的影响会使得定位的稳定性受到较大的影响，非线性的最小二乘法同样也存在与极大似然计算法的问题。因此为了进一步的提高目标定位的计算精度，本文将极大似然法作出了进一步的优化，以实现目标定位的有效性。

1.1 声音能量模型

声音能量模型的建立主要是声音信号在传播过程中声音的强弱以及传播的距离之间的关系模型，能量目标的定位方法是建立在声音能量模型的基础上对传感器节点接受到的信号能量进行计算，然后估计目标源的位置。因此在实现目标位置时可以建立一个声音能量模型，然后假设传感器节点，将其组成一个无线传感器网络，然后测量某一位置声音信号的能量。

1.2 基于极大似然估计定位的方法分析

在计算目标定位时可以以已知信号能量模型为基础，采用极大似然的方法进行计算并求解。由此可以得到矩阵形式为Z=GDS+ξ=HS+ξ，然后采用似然函数f(Z/θ)达到最大值θ值 ，最后等价求出L(θ)ⅡZ-HSⅡ²达到最小值 。L(θ)ⅡZ-HSⅡ²是一个非线性二次方程式，在求解的过程中需要采用二次最优化方法。而且这种方法在多目标计算求解的过程中可以在定位精度不受影响的情况下，可以起到减少计算量的作用。

2 最优化极大似然定位方法的分析

关于基于无线传感器目标定位计算方法的研究中，有外国学者提出了最优化极大似然定位的方法。最优化极大似然估计其公式表达如，θ=argmax{-E[logp(Z/θ)]}。其中 E[logp(Z/θ)是对数似然函数的期望值的计算，而且这个公式是渐进有效的，所以当观察的数据越多，趋于实际分布所期望的对数似然就会越高。进一步说明了极大似然的计算方法在计算目标定位时能实现最优的估计，实际分布如果能够得出实际求解值，E[logp(Z/θ)就能得到相应的计算值，也就能得到公式所表达的最优化最大似然估计量。但是如果在有限的样本上找出实际分布式行不通的，因此在计算的过程中可以以使平方和偏差最小化原则为基础，然后通过似然函数得出一个特定值。基于最优化极大似然估计的定位方法实际是将最优化极大似然应用到声音信号能量模型中，然后根据似然函数的实际分布最佳近似分布得出最后的矩阵形式为S=HZ。采用最优化似然的计算方法能够在准则下得到最优解θ，也就得到了相应的目标位置。

3 实验结果分析

在上述研究探讨中有提到最大似然算法和非线性最小二乘法以及声音能量计算方法，似然计算方法进行仿真计算，然后将几种计算方法的性能进行比较。并将N个传感器节点分布在一个100mx100m的区域中，根据有公式可以得到设定目标源的能量为S=5000。在仿真实验研究和分析的过程中需要将最近点定位计算方法，极大似然定位方法和非线性最小二乘定位法以及最优化极大似然定位方法的结果进行了2000次的计算。在计算的过程中每次都会得到一个定位估计和估计误差值，然后将得到的误差值进行和协方差。如下表所示各计算方法的误差均值以及和协方差：

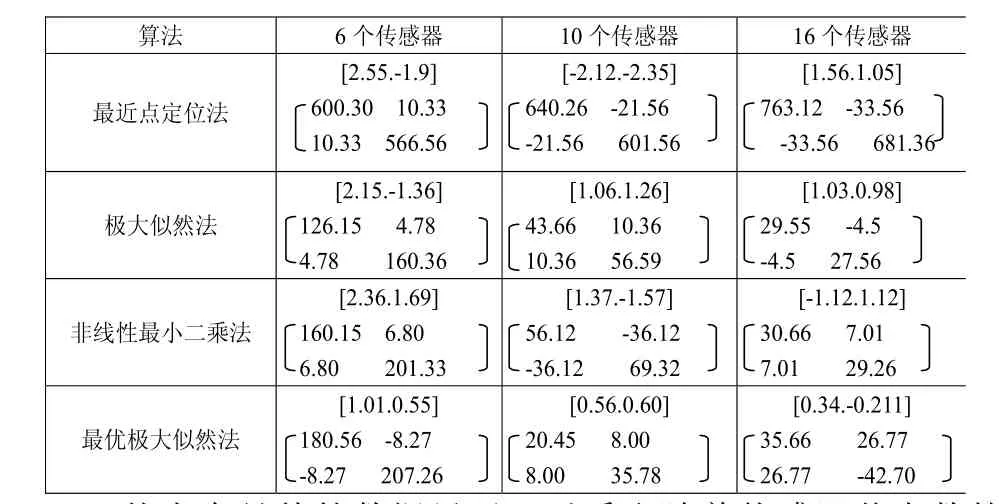
从表中具体的数据显示可以看出随着传感器节点数的增加，其定位计算方法得出的误差均值也在相应的减少。从中也可以出最优化极大似然定位计算方法要比其他的三种计算方法得出的误差均值小，而且其目标定位精度也比其他三种计算方法更加准确。为了进一步的证明最优极大似然定位计算方法性能的稳定性和高精确度，有关研究人员对关于估计位置与实际位置距离差，其中以5米为一个单位呈现递增的趋势进行了研究和分析，结果发现最优极大似然定位计算方法在目标定位应用中具有一定的可靠性和有效性。

关于无线传感器目标定位的计算方法还有很多种，同样有一种方法是在二维空间中对声源的进行定位，定位的结果是定位的目标对象相对网络节点之间的距离和角度。一般在对声源进行定位时需要在无线传感网络节点中选取至少三个节点数，然后以定位的目标对象相对网络节点之间的距离和角度为基础进行三维空间的推广计算。当然也可以从无线传感网络节点数中选取2个节点对声源的曲线情况进行确定，在计算过程中如果能够得到两条以上的曲线基本上定位目标的位置已经确定。关于无线传感器网络目标定位算法还有很多需要根据现代科学技术做出进一步的研究，实现目标定位的稳定性和有效性。

结束语

在上述研究分析过程中最优极大似然的目标定位计算方法得出的定位定都具有一定的可靠性和有效性，并实现了其性能的稳定性。最优极大似然目标定位法是在极大似然定位法的基础上提出的，这种定位计算得出的结果其误差要比其他三种计算方法得出的误差要小，而且精度高，定位性能具有一定的稳定性特点。最优极大似然在上述研究过程中主要是对单目标进行定位，并得到了最佳的效果，但是关于多目标定位还需要作出进一步的研究。

[1]刘桂雄,张晓平,周松斌.基于最小二乘支持向量回归机的无线传感器网络目标定位法[J].光学精密工程.2009(7).

[2]张晓平,刘桂雄,周松斌.利用最小二乘支持向量机实现无线传感器网络的目标定位[J].光学精密工程.2010(9).

[3]周德超,吴晓平,张鹏鹰.二进制无线传感器网络目标定位解析算法初步研究[J].海军工程大学学报.2007(5).

[4]林金朝,李国军,周晓娜,周道军,蒋勇.基于动态能量管理的无线传感网络动目标定位跟踪方法[J].通信学报.2010(12).

[5]唐国明,周广新,谢羿,汤大权,唐九阳.一种基于双层栅格划分的无线传感器网络目标定位方法[J].计算机科学.2012(6).

[6]蔡志强,谷雨,胡燏翀,许胤龙.一种无信标无线传感器网络中的目标定位策略[J].计算机应用.2007(8).