压电陶瓷迟滞非线性的成因与校正

史丽萍，魏艳波，魏喜雯，张 波，徐艳春，瞿晓东

（黑龙江大学 机电工程学院，哈尔滨 150080）

0 引言

目前广泛应用的压电陶瓷有钛酸钡（Ba－TiO3）、钛酸铅（PbTiO3）、锆钛酸铅（PZT）等。利用其制成的压电陶瓷微位移执行器具有许多其它执行器没有的优点，克服了以往机械式、液压式、气动式、电磁式等驱动器惯性大、响应慢、可靠性差等不足，具有位移分辨率高、机电耦合效率高、响应快、功耗小、无噪声等。从而被广泛应用于精密定位技术中。但它同时也存在着明显的不足，在电场的作用下输出的位移会产生迟滞非线性，这样极大地降低了它在微纳米执行技术中的定位精度［1－3］。

压电陶瓷在电场的作用下有铁电效应、电致伸缩效应、逆压电效应。由于压电陶瓷的电致伸缩效应对位移的影响极其微弱，可以忽略不计［4］，而其逆压电效应又是线性的，所以压电陶瓷执行器的迟滞非线性是由铁电效应产生的。本文通过分析压电陶瓷在外电场作用下铁电效应对压电陶瓷执行器的位移产生的影响，以确定压电陶瓷迟滞产生的原因。并提出一种有效的方法对压电陶瓷位移进行误差补偿，以实现压电陶瓷执行器与控制信号具有较好的线性对应关系。

1 压电陶瓷的铁电效应

压电陶瓷是属于铁电材料的压电体，具有一般铁电材料所具有的共性：迟滞非线性。铁电材料在外电场为零时，具有自发极化的现象，压电陶瓷中单位晶胞的固有偶极矩沿同一方向整齐排列，使压电陶瓷晶体处于高度极化状态。铁电材料中的自发极化总是会分裂成一系列极化方向不同的小区域，使自发极化在外部空间建立的电场相互抵消，因而整个单晶体对外不显电性。这些自发极化相同的小区域称为电畴。自发极化的电畴会在外电场的作用下重新取向，这种在外电场作用下，使压电陶瓷晶体自发极化重新取向的状态称为铁电效应［5］。

压电陶瓷具有类似铁磁材料磁畴结构的电畴结构，在没有预极化处理前，各个电畴在晶体中杂乱分布，它们的极化效应被相互抵消，内部极化强度为零，见图1（a），所以压电陶瓷使用之前要进行人工极化。在强直流极化电场作用下，电畴的极化方向以外电场方向充分排列，见图1（b）。去掉电场后，经预极化处理后电畴会大致沿一个方向，但并没有完全转向与电场一致的方向，压电陶瓷内部仍存有很强的剩余极化强度，见图1（c）［6］。

图1 压电陶瓷的极化处理Fig.1 Polarization treatment of the piezoelectric ceramic

2 压电陶瓷的迟滞成因分析

设极化后的第i个电畴的轴长为li，极化后自发极化方向与电场方向的夹角为βi。给压电陶瓷施加驱动电压，便会在压电陶瓷外部产生电场，这时电场作用下自发极化方向与电场方向之间的夹角为αi，见图2。电畴在电场作用下转向的相对位移为［7］：

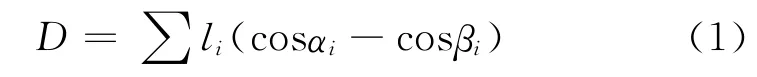
式中li，βi是常量，αi则随场强变化。

在αi处对cosαi进行泰勒展开为：

图2 压电陶瓷在电场作用下的位移Fig.2 Displacement of the piezoelectric ceramic under electric field

可见式（2）是非线性的。当准静态电压逐渐升高时，场强变大，αi变小，αi－βi变大，从而电压——位移的上升曲线呈现较大的非线性，见图3（HPV 压电陶瓷驱动电源提供驱动电压，MPT－2MRL103A 纳米级精密定位工作台输出位移）。

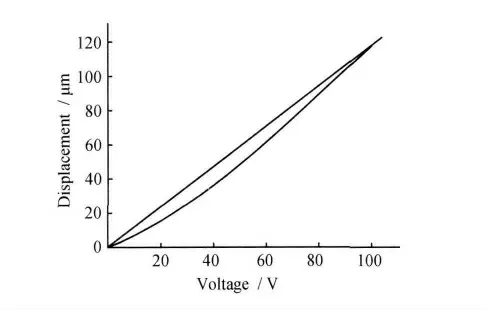
图3 压电陶瓷电压－位移上升曲线Fig.3 Voltage－displacement rising curve of piezoelectric ceramic

经预极化处理的压电陶瓷内一端出现正束缚电荷，一端出现负束缚电荷，由于束缚电荷的作用，会在压电陶瓷内产生附加电场E1，见图4（a）。设外部准静态电压每增加10V 产生的场强为ΔE1，因此合成场强为ΔE＝ΔE1＋E1。电畴之所以能在外电场的作用下重新取向，其自身必定存在一个自发电场，设第i个电畴的自发电场为Ei，此时陶瓷内部所受电场见图4（b）。在准静态电压增加的过程中，只考虑第i个电畴产生的电场与外加电场的作用，合成的场强E1i见图4（c），电畴因此会朝向E1i方向转动，准静态电压再增加10V 后，电畴的转向会沿ΔE＝ΔE1＋E1和E1i的合成场强E2i方向转动，见图4（d），以此类推。因此，压电陶瓷输出的位移就如图3所示的过程，具有较大的非线性。

当准静态电压达到最大值开始减小时，相当于给压电陶瓷施加一个与极化方向相反的电压或电场，每减小10V，产生的电场与增加过程的电场大小相等，方向相反，由于这种电荷不像导体中的自由电荷那样可以自由移动，所以束缚电荷产生的电场保持不变，垂直方向总电场为ΔE′＝ΔE1′－E1，E1起着削弱外电场的作用。因此在图4（d）的基础上ΔE′＝ΔE1′－E1和E2i的合场强为E1′i，电畴沿E1′i转向，见图4（e）。由此可知准静态电压减小与准静态电压增大到同一电平时产生的合场强不同，相对于电场增加的过程中，减小过程电场转向要比同一电平时电场增加过程更偏向施加的外电场方向，电畴偏离的要小，因此输出的位移大于同一电平时电场增加时的输出位移，从而压电陶瓷的电压——位移曲线产生严重的迟滞现象。压电陶瓷执行器的静态位移特性曲线见图5（HPV 压电陶瓷驱动电源提供驱动电压，MPT－MRL103A 纳米级精密定位工作台输出位移）。

图4 压电陶瓷中电畴所受电场分析Fig.4 Analysis on electric field of domain in piezoelectric ceramic

图5 压电陶瓷执行器的静态位移特性曲线Fig.5 Static displacement characteristic curves of piezoelectric actuator

同时，由于电畴在电场下的极化转向或重新定位通过畴壁的移动和新畴壁的产生及运动来完成。畴壁的运动和新畴壁的产生必定产生热量，使压电陶瓷温度发生变化，自发极化强度随着温度的升高而下降，由于离子间距和键角发生变化，这时被自发极化束缚在表面的自由电荷就有一部分可以恢复自由释放出来，使晶体呈现带电状态，产生与原电场相反的电场。总的电场减小，压电陶瓷的电压——位移曲线产生迟滞现象，也是引起曲线最终不能回到零点的原因。

3 压电陶瓷执行器迟滞非线性的改善方法

压电陶瓷执行器的迟滞非线性补偿控制方法主要可分为：逆补偿和闭环控制。逆补偿控制方法是指对迟滞特性建立逆模型对迟滞系统进行解耦，以降低设计控制器的难度。迟滞模型一般分为两种：①基于机理的物理模型，如Maxwell模型，Jiles－Atherton模型，Duherm 模型等；②基于现象的数学模型，或称唯象数学模型，如Preisach 模型，Prandtl－Ishlinskii模型等。闭环控制无需建立迟滞非线性逆模型进行补偿，而是在控制器的执行器设计过程中直接考虑迟滞非线性对系统性能的影响［8］。

本文采用压电陶瓷执行器平台 MPTMRL103A，此平台内部安装电阻应变传感器，采用HPV 压电陶瓷驱动电源提供驱动电压，测试压电陶瓷执行器的静态、动态输出位移特性。在分析执行器输出特性的基础上建立执行器制动模型，并利用此模型＋PID 反馈控制来校正压电陶瓷的迟滞非线性。

3.1 广义非线性Preisach模型

为了解决压电陶瓷执行器输出迟滞给控制系统带来的误差，采用广义非线性Preisach 模型建立压电陶瓷执行器的迟滞模型。经典Preisach 模型的一般表达式为［9］：

式中f（t）为函数在t时刻的迟滞输出；u（t）为t时刻的输入电压；γαβ［u（t）］为基本迟滞算子；μ（α，β）为Preisach函数，α，β分别为其上升和下降阈值。

压电陶瓷的迟滞特性很好地满足了擦除特性，但是在极大值和极小值相同的两组电压下所得到闭合回线不相等，不能直接应用经典Preisach 模型对压电陶瓷执行器的迟滞特性进行建模。在经典Preisach模型的基础上，Mayergoyz提出了非线性Preisach模型［10］，针对压电陶瓷的输入输出特性对非线性Preisach 模型进行修改，可得到应用于描述压电陶瓷特性的广义非线性Preisach 模型，其数学表达式如下：

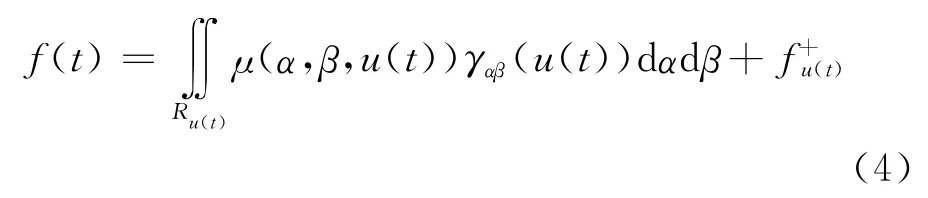
在输入上升过程中，所有具有上升阈值α：α＜u（t）的迟滞算子γαβ（u（t））的输出值均变为1。因此，上式可简化为：

广义非线性Preisach 模型中需要利用一阶和二阶回转曲线进行辨识，定义F（α′，β′，u（t））为输入电压为u（t）时一阶回转曲线上的位移和二阶回转曲线上的位移之差，即：

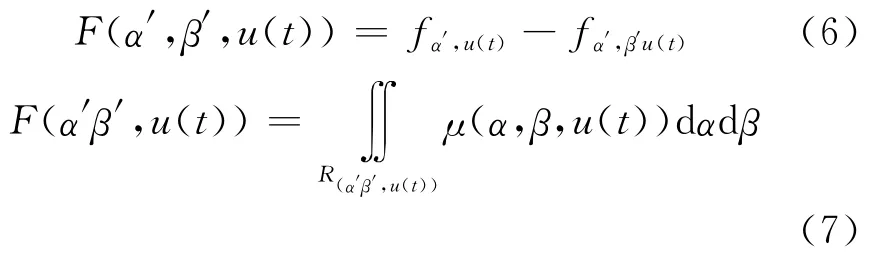
对上式两边求二次导数，再经过进一步推导，可得压电陶瓷执行器迟滞环的上升曲线和下降曲线的广义非线性Preisach模型的离散数学公式［11］：

利用广义非线性Preisach 模型离散表达式对压电陶瓷迟滞特性进行建模，其模型见图6。模型的理论曲线与图5 的执行器输出特性曲线基本吻合。

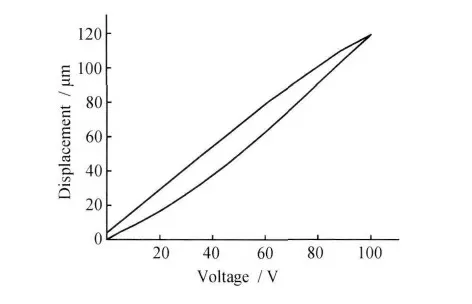
图6 广义非线性Preisach迟滞模型仿真曲线Fig.6 Simulation curves of generalized nonlinearity Preisach model

3.2 基于广义非线性Preisach模型前馈＋PID 反馈控制

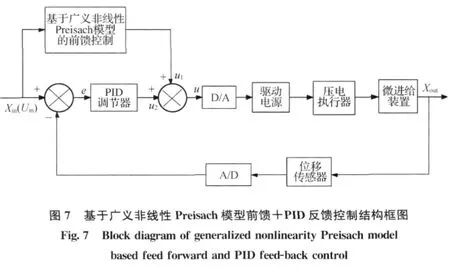
基于广义非线性Preisach模型的前馈控制极大地改善了压电陶瓷执行器的迟滞非线性，减小了实际输出与预期输出之间的偏差。PID 控制策略具有较好的鲁棒性和无需精确建模的特点，在精密定位控制系统中被广泛采用。为了实现压电陶瓷执行器既快速又高精度的定位，引入闭环反馈和基于广义非线性Preisach 模型的前馈控制环节。根据经典控制理论，合适的前馈控制环节可提高系统的控制响应能力，但不影响系统的最终控制精度。图7为带前馈的PID 闭环控制的结构框图［12］。

图7中Uin为要求的输出位移Xin对应的电压信号；Xout为执行器的实际输出位移；u1为与要求的输出位移对应的迟滞非线性Preisach 模型的前馈环得到的控制电压；u2为PID 算法将Xin与输出值Xout的差值进行比例、积分和微分运算后得到的控制电压。u1和u2相加得到最终的控制电压u送数据采集卡，经D／A 转换后产生一个低电压信号，经驱动电源使压电驱动器产生伸缩变形。通过A／D 转换其读取微位移传感器的值再与设定值进行比较，进行下一次PID 控制，直至满足指定控制精度要求［13］。

经广义非线性Preisach 模型前馈和PID 反馈控制校正后，压电陶瓷执行器的静态位移特性曲线见图8。

4 结语

压电陶瓷迟滞特性是影响压电陶瓷执行器位移输出精度的主要因素。本文通过分析压电陶瓷的铁电效应的微观极化机理，解释了压电陶瓷迟滞非线性产生的原因：①电畴的转向理论；②由束缚电荷产生的电场。并采用广义非线性Preisach模型前馈＋PID反馈控制，改善压电陶瓷执行器的迟滞特性，提高其控制精度。

［1］TAN X，BARAS JS.Modeling and control of hysteresis in magnetostrictive actuators［J］.Automatica，2004，40（9）：1 469－1 480.

［2］BANKS H T，SMITH R C.Hysteresis modeling in smart material systems［J］.Appl.Mech.Eng，2000，（5）：31－45.

［3］G.Tao，P V Kolotovic.Adaptive control of plants with unknown hysteresis［J］.IEEE trans.Automatic Control，1995，40（2）：200－212.

［4］钟维烈.铁电体物理学［M］.北京：科学出版社，1996：391－394，294－297.

［5］张福学，王丽坤.现代压电学［M］.北京：科学出版社，2002：134－138.

［6］史丽萍.多次压电效应探析及在传感执行器上的应用基础研究［D］.大连：大连理工大学，2006：80－83.

［7］崔玉国，孙宝元，董维杰，等.压电陶瓷执行器迟滞与非线性成因分析［J］.光学精密工程，2003，11（3）：270－275.

［8］赖志林，刘向东，耿 洁，等.压电陶瓷执行器迟滞的滑膜逆补偿控制［J］.光学精密工程，2011，19（6）：1 281－1 282.

［9］MAYERGOYZID.Mathematical models of hysteresis［M］.New York：Springer－Verlag，1991.

［10］GE P，JOUANEH M.Generalized Preisach model for hysteresis nonlinearity of piezoceramic actuator［J］.Precision Engineering，1997，20（2）：99－111.

［11］李 黎，刘向东，王 伟.压电陶瓷执行器迟滞特性的广义非线性Preisach模型及其数值实现［J］.光学精密工程，2007，15（5）：707－710.

［12］谭志波.压电陶瓷驱动器迟滞补偿方法研究［D］.哈尔滨：哈尔滨工业大学，2008：22－27.

［13］韩同鹏，李国平，沈 杰.基于压电陶瓷微位移执行器的精密定位技术研究［J］.传感器与微系统，2010，29（2）：51－53.