基于弹性网回归的居民消费价格指数分析
张 哲,梁冯珍
(天津大学 理学院数学系,天津300072)
回归分析是数理统计中的一类重要研究课题.近几十年来,回归分析技术已被广泛应用于工农业、水文气象、经济管理、医药卫生等领域.然而,随着现代科学技术的不断进步,数据收集技术也得到了很大程度的提高.所以,对于某些特定类型的数据,原始的线性回归方法已不再适用,这就需要学者们研究更多其他可行的方法.
在传统的线性回归模型中,最小二乘估计(LS)应用最为广泛,这是因为在所有线性无偏估计类中,LS估计的方差最小.然而,由于近年数据收集技术的提高,使得数据拥有大量的预测变量,而预测变量之间常常存在某些线性关系,导致设计矩阵呈病态.若仍采用LS估计,尽管它在线性无偏估计类中方差最小,但其估计不稳定且精度较差.近年来,基于最小二乘估计,许多学者提出了多种改进方法,其中很重要的一部分就是有偏估计,即以很小的偏倚为代价,降低估计值的方差,使得总体的期望预测误差大幅度减少,从而提高估计的精度与稳定性.
早期对LS估计的改进方法有岭回归估计、子集选择等.其中,岭回归估计是指通过对LS估计中的残差平方和加二次罚,达到收缩估计系数的目的.岭回归的估计结果包含了所有的变量,且变量的系数均小于LS的估计值.1996年,Tibshirani提出了一种新的回归方法——Lasso(Least absolute shrinkage and selection operator)[1].这种方法看似简单的将岭回归的二次罚修改为一次罚,但在用二次规划求解Lasso的过程中,一些变量的系数会自动收缩到0,从而达到变量选择的目的,且估计具有一定的稳定性.近年来,在Lasso的基础上,很多统计学家提出了更多的改进方法,如文献[2-6],Elastic Net方法[7]同时具有岭回归和Lasso回归的性质,特别对具有群组性的预测变量,估计效果更好.
居民消费价格指数是国民经济中的重要指标,其变动率在一定程度上反映了国家通货膨胀(或紧缩)的程度以及对职工实际工资的影响,即职工工资保持不变的情况下,居民价格消费指数提高意味着实际工资减少.因此,本文对居民价格消费指数与行业物价指数建模并分析,有很强的实际意义.
本文首先介绍并讨论了岭回归、Lasso回归、E-lastic Net回归三种方法,然后分别用这三种方法对中国统计年鉴中2001~2010年的居民消费指数和行业物价指数数据进行分析、建模,结果表明,E-lastic Net回归的效果最好.
1 线性回归模型的三种估计方法的性质
线性回归是回归分析中最基本的一类回归问题.对于一般的线性模型来说,假设预测变量的个数为p,样本容量为N,则

若记 Y=(y1,y2,…,yN)T,β =(β0,β1,…,βp)T,Xi=(x1i,x2i,…,xNi)T,i=1,2,…,N,X=(1,X1,X2,…,Xp),ε =(ε1,ε2,…,εN)T,T 代表转置,则模型(1)用矩阵表示为

故回归系数的最小二乘估计为βLS=(XTX)-1XTY.对任意给定 x0=(x01,x02,…,x0p)T其拟合值
对于给定的x=x0,拟合值^Y=^f(x0)的期望误差分解如下:
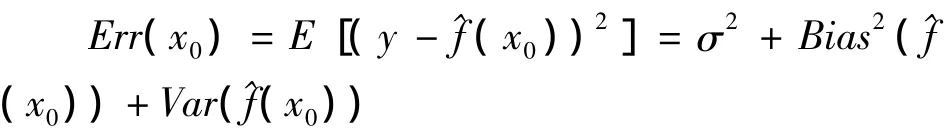
其中:E(y)=f(x0),σ2为目标值围绕真实值的一个扰动,无论模型估计的有多好,这一项都不可避免的出现,Bias2(^f(x0))为偏倚,即为估计值偏离真实值的一个度量,Var(^f(x0))为估计值的方差.
1.1 岭回归(Ridge Regression)
对于模型(1),岭回归估计的定义为:

其中:λ≥0为罚参数,λ取值越大,回归系数收缩越大.特别地,当λ=0时,岭回归退化为LS回归.值得注意的是,在惩罚项中,并没有对常数项β0进行惩罚.事实上,对每一个响应加上一个常数,不会对回归系数造成影响.从而,岭回归的解式(3),可以分为两部分,一部分是对响应变量Y中心化,得到常数项β0的估计值为,另一部分是用岭回归定义估计其他预测变量的系数.
将响应变量中心化后,式(3)等价为
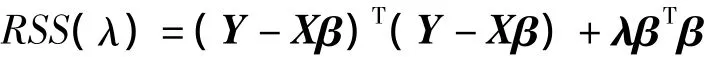
解优化问题minRSS(λ)得岭回归的解为

由式(5)可以看出,岭回归的解是在LS回归解的基础上,加了一个正的惩罚参数λ.故当矩阵X的某些列向量近似线性相关时,矩阵XTX+λΙ的奇异性要比XTX低,从而降低了估计值的方差,提高了估计精度.然而,岭回归也有一定的局限性,它的回归结果中包含所有的预测变量,没有进行变量选择,因此会影响模型的准确性.
1.2 套索(Lasso)
针对岭回归中没有变量选择的问题,Tibshirani在1996年提出了Lasso回归,对其进行了改进.Lasso估计的定义为

下面分别采用岭回归和Lasso回归对R软件包ElemStatLearn中的prostate数据进行分析,该数据样本数量为97,包含一个响应变量(lpsa)和8个预测变量(lcavol,lweight,age,lbph,svi,lcp,gleason,pgg45).岭回归和Lasso回归的求解途径如图1所示.

图1 岭回归与Lasso回归的求解路
其中图1左为岭回归的求解路径,横坐标为自由度(即回归变量个数),纵坐标为预测变量系数.图1右为Lasso回归的求解路径,横坐标为变换后的收缩因子|,其中 s∈[0,1],t为式(6)中回归系数之和的限制值.显然,岭回归没有达到变量选择的目的,Lasso回归随着收缩因子s的不断增大,逐渐有预测变量系数变为0,故具有变量选择的功能.
1.3 弹性网(Elastic Net)
Lasso回归与LS回归相比虽然大大降低了预测方差,达到了系数收缩和变量选择的目的,但是也有一定的局限性 I[9-12],譬如
1)在Lasso回归求解路径中,对于N×p的设计矩阵来说,最多只能选出 min(N,p)个变量[2].当p>N的时候,最多只能选出N个预测变量.因此,对于p~N的情况,Lasso方法不能够很好的选出真实的模型.
2)如果预测变量具有群组效应,则用Lasso回归时,只能选出其中的一个预测变量.
3)对于通常的N>p的情形,如果预测变量中存在很强的共线性,Lasso的预测表现受控于岭回归.
基于以上几点Lasso回归的局限性,Zou和Hastie在2005年提出了弹性网回归方法,回归系数表达式为

2 实证分析
下面将分别采用岭回归、Lasso回归和弹性网回归三种方法对中国统计年鉴中从2001年到2010年近10年来中国的居民价格消费指数(CPI指数)[10]和46种行业物价指数进行分析,并通过建立模型,来研究各种物价指数对居民价格消费指数的影响.变量内容详见参考文献[13].所有的计算均采用R和Matlab软件计算.
首先,给出岭回归、Lasso回归和弹性网回归3种方法的求解路径,如图2所示.
由图2知,岭回归的预测变量回归系数随着罚系数λ的增大逐渐减小,且所有回归系数均不为0,甚至许多预测变量系数为负数,这不符合经济学规律;对于某一特定罚系数λ,Lasso回归把某些预测变量回归系数收缩为0,从而达到了变量选择的目的.因此Lasso回归比岭回归更优越.
其次,给出λ取不同值时,预测变量的回归系数如表1、2所示(因为岭回归的回归系数都不等于零,所以略去预测变量的回归系数表示,从图2中可大致看出估计结果).
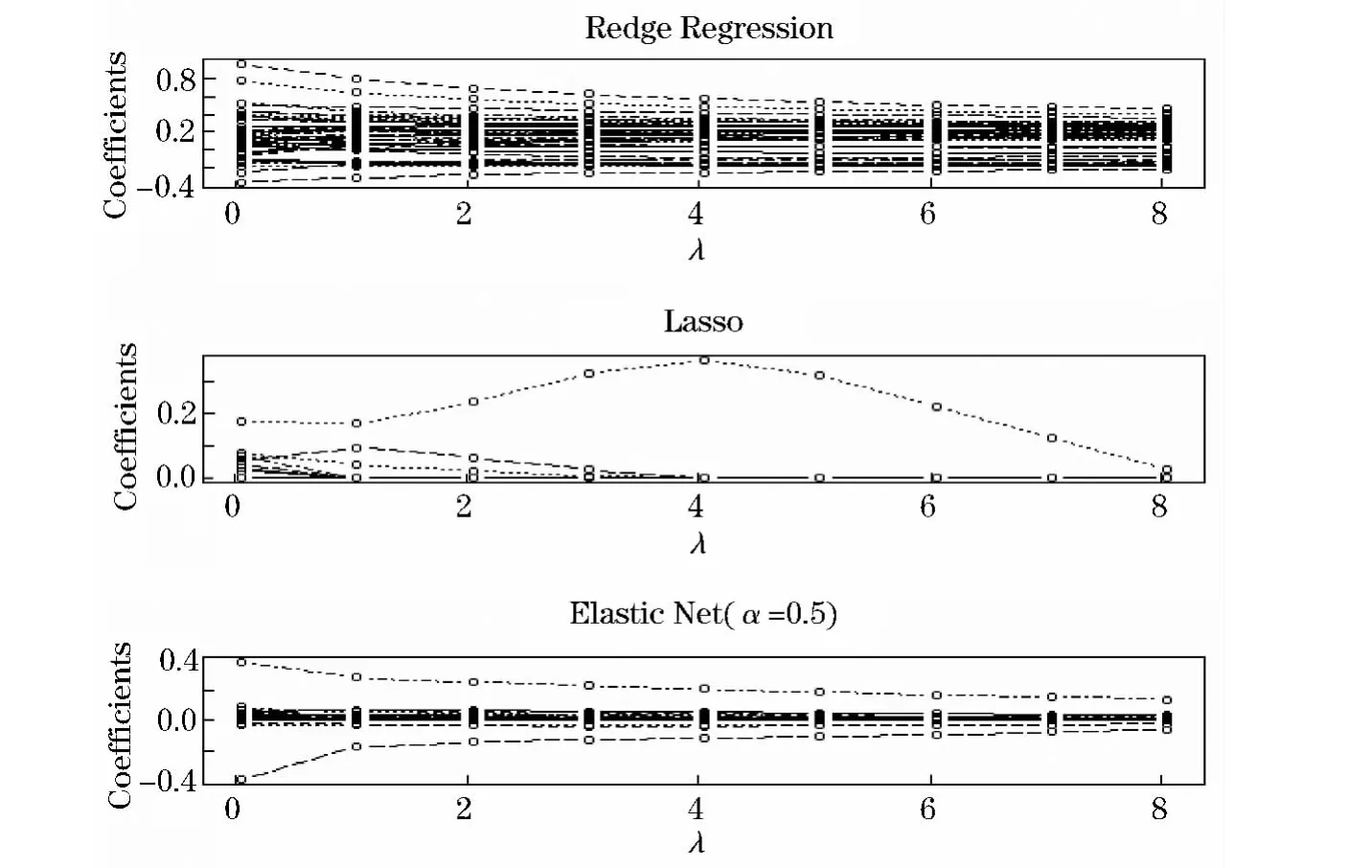
图2 三种回归方法的求解路径图
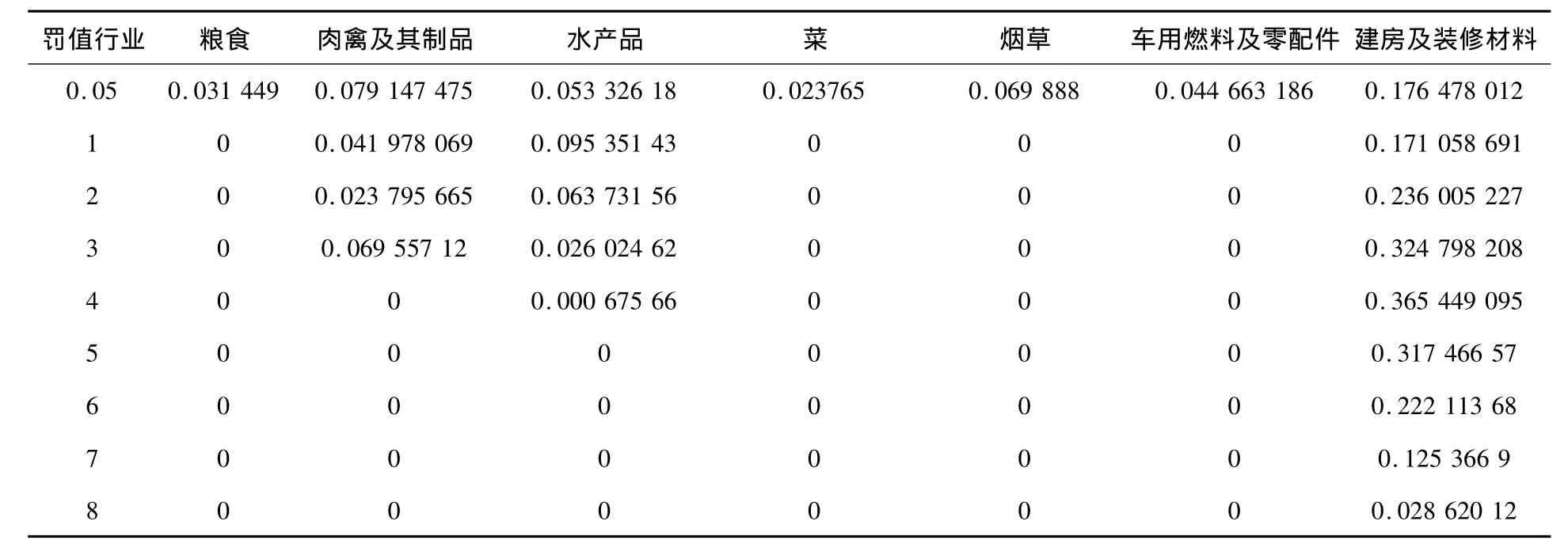
表1 罚系数不断增大时Lasso方法的回归系数,其他变量系数为0
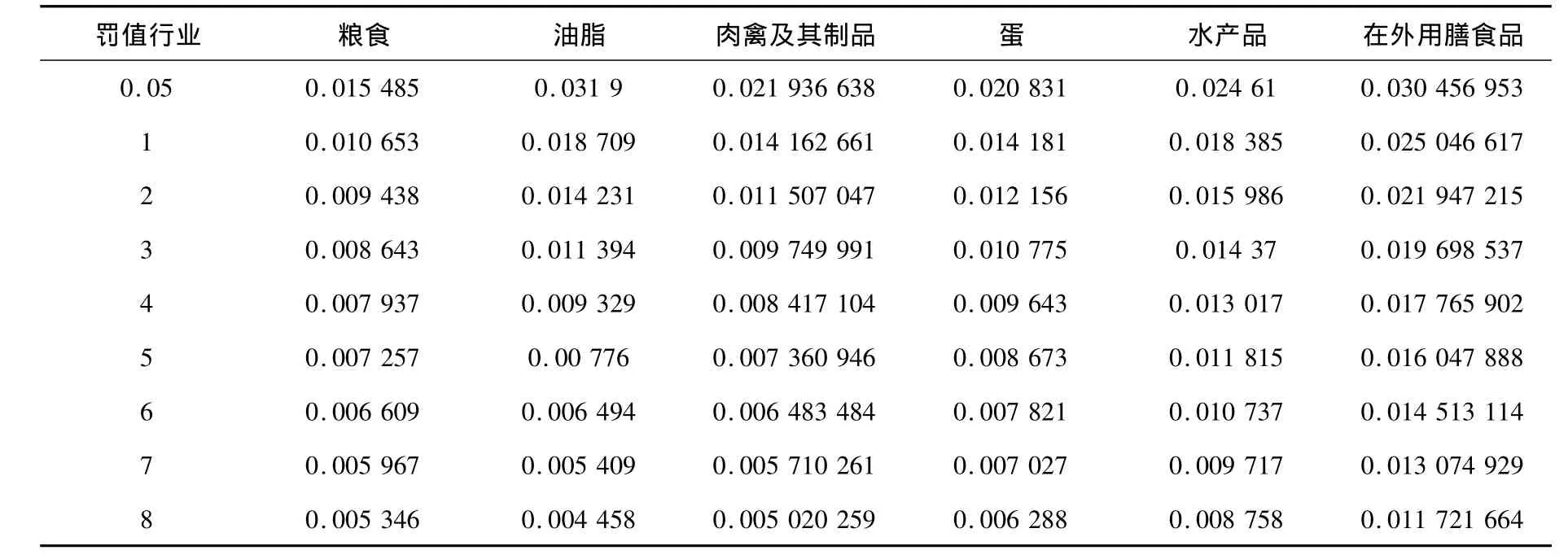
表2 罚系数不断增大时Elastic net方法预测变量回归系数
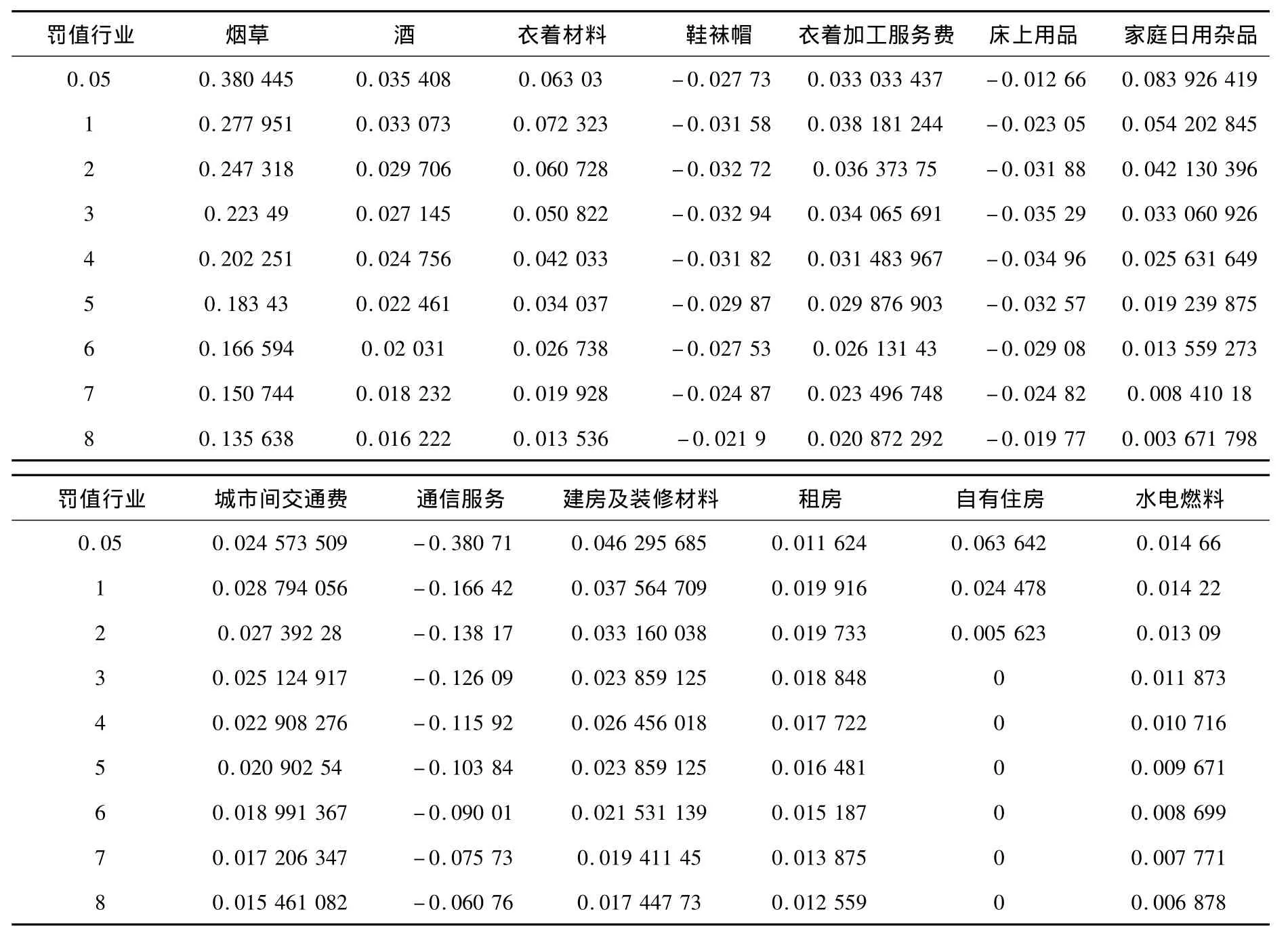
罚值行业 烟草 酒 衣着材料 鞋袜帽 衣着加工服务费 床上用品 家庭日用杂品0.05 0.380 445 0.035 408 0.063 03 -0.027 73 0.033 033 437 -0.012 66 0.083 926 419 1 0.277 951 0.033 073 0.072 323 -0.031 58 0.038 181 244 -0.023 05 0.054 202 845 2 0.247 318 0.029 706 0.060 728 -0.032 72 0.036 373 75 -0.031 88 0.042 130 396 3 0.223 49 0.027 145 0.050 822 -0.032 94 0.034 065 691 -0.035 29 0.033 060 926 4 0.202 251 0.024 756 0.042 033 -0.031 82 0.031 483 967 -0.034 96 0.025 631 649 5 0.183 43 0.022 461 0.034 037 -0.029 87 0.029 876 903 -0.032 57 0.019 239 875 6 0.166 594 0.02 031 0.026 738 -0.027 53 0.026 131 43 -0.029 08 0.013 559 273 7 0.150 744 0.018 232 0.019 928 -0.024 87 0.023 496 748 -0.024 82 0.008 410 18 8 0.135 638 0.016 222 0.013 536 -0.021 9 0.020 872 292 -0.019 77 0.003 671 798罚值行业 城市间交通费 通信服务 建房及装修材料 租房 自有住房 水电燃料0.05 0.024 573 509 -0.380 71 0.046 295 685 0.011624 0.063 642 0.014 66 1 0.028 794 056 -0.166 42 0.037 564 709 0.019 916 0.024 478 0.014 22 2 0.027 392 28 -0.138 17 0.033 160 038 0.019 733 0.005 623 0.013 09 3 0.025 124 917 -0.126 09 0.023 859 125 0.018 848 0 0.011 873 4 0.022 908 276 -0.115 92 0.026 456 018 0.017 722 0 0.010 716 5 0.020 902 54 -0.103 84 0.023 859 125 0.016 481 0 0.009 671 6 0.018 991 367 -0.090 01 0.021 531 139 0.015 187 0 0.008 699 7 0.017 206 347 -0.075 73 0.019 411 45 0.013 875 0 0.007 771 8 0.015 461 082 -0.060 76 0.017 447 73 0.012 559 00.006 878
从表2中可以看出,弹性网选出的变量个数介于Lasso回归和岭回归之间,既达到了很好的变量选择效果,又保留了原有数据的群组效应.即某些相关性很强且很有价值的变量(如粮食、肉禽、水产品、蛋类等)的系数均不为0,而某些相关性很强但不是很有价值的变量(化妆美容用品、清洁化妆用品以及保健器具及用品、医疗保健服务等)的系数均为0.Lasso回归至多选出7个预测变量,小于样本量个数,而弹性网回归选出了更多的变量,不仅具有群组性,而且保证了模型的真实性.
最后,弹性网回归对于不同的取值所表现出的不同性质,见图3.

图3 L 1罚和L2罚不同比例Elastic Net路径图
从图3可以看出α的取值影响弹性网回归的求解路径,当α的取值偏小时,弹性网回归表现出类似岭回归的性质,当α的取值偏大时,表现出类似Lasso回归的性质.
3 结语
岭回归结果表明,2001~2010年国内影响CPI指数的主要行业物价指数有食用类(粮食、肉脂、肉禽及其制品、蛋、水产品)和住房类(建房及装修材料、租房、自有住房、水电燃料),其他行业物价指数均有影响,但所占比重不大.岭回归虽然一定程度上刻画了国内近十年来的真实情况,即居民消费主要集中在吃住,但并没有删除其他影响不大的行业价格指数,回归结果失真;根据表1,Lasso回归结果表明,影响居民消费价格指数的主要物价指数是建房及装修材料、肉禽及其制品、水产品,其中建房及装修材料最为突出.这反映了影响CPI指数的主要行业物价指数,符合实际情况,但是去掉了大部分其他的行业物价指数,使模型过于简洁,显然不符合实际情况.根据表2,弹性网回归结果表明,该方法一方面达到了岭回归对重要种类(衣、食、住、行、用)中几种具有代表性的行业价格指数选择的目的,另一方面又像Lasso回归一样,删除了其他影响很小的行业物价指数,取得了最好的效果.由此可知,衣食住行用这几大产业,支撑着中国国民经济,与人们的生活息息相关,在各行各业当中占有重要地位.
[1]TIBSHIRANIR.Regression shrinkage and selection via the lasso[J].Journal of the Royal Statistical Society,Series B,1996,58(1):267-288.
[2]FAN J,LIR Z.Variable selection via penalized likelihood[J].Journal of American Statistical Association,2001,96(4):1348-1360.
[3]SAUNDERS M.Sparsity and smoothness via the fused lasso[J].Journal of the Royal Statistical Society,Series B,2005,67(l):91-108.
[4]HUANG J,MA S,ZHANGCH.Adaptive Lasso for sparse high-dimensional regression models[R].Iowa:University of Iowa Department of Statistics and Actuarial Science,2006,Technical Report No.374.
[5]YUAN M,LIN Y.Model selection and estimation in regression with Grouped variables[J].Journal of the Royal Statistical Society,Series B,2006,68(l):49-67.
[6]MEINSHAUSEN N.Relaxed Lasso[J].Computational Statistics and Data Analysis,2007,52(1):374 -393.
[7]ZOU H,HASTIE T.Regularization and variable selection viathe elastic net[J].Journal of the Royal Statistical Society,2005,Series B,67(l):301- 320.
[8]HASTIE T,TIBSHIRANI R,FRIEDMAN J.The Elements of Statistical Learning:Data Mining,Inference and Prediction[M].NEW YORK:Springer,2008.
[9]HESTERBERG T,NAM H C,LUKAS M,etal.Least angle and penalized regression:A review [J].Statistics Surveys,2008,2(2008):61–93.
[10]ZOU H.Adaptive Lasso and its Oracle Properties[J].Journal of American Statistical Association,2006,101(3):1418 -1429.
[11]熊 英.基于Lasso的人脸识别算法[D].北京:清华大学,2010.
[12]龚建朝.Lasso及其相关方法在广义线性模型选择中的应用[D].长沙:中南大学,2008.
[13]中华人民共和国国家统计局.中国统计年鉴-2011[M].北京:中国统计出版社,2011.

