模糊自适应PID控制在主动磁悬浮系统中的研究
郑仲桥,张燕红
(1. 常州工学院 电子信息与电气工程学院,常州 213002;2. 上海大学 机电工程与自动化学院,上海 200072)
0 引言
由于主动磁悬浮轴承能够实现非接触支承,具有无机械磨损、无需润滑、工作温度范围大、工作极限转速高等优点,在国内外得到了迅速的发展,已经在军工、航天等国防工业部门中逐步应用,并向民用工业,如航空、机床、化工、能源等工业领域推广[1,2]。但是在主动磁悬浮控制系统中,由于电磁铁磁性材料的非线性及外界干扰信号的影响,使得主动磁悬浮控制系统是一个典型的非线性、参数不确定的控制系统,以往使用的常规PID控制算法很难使系统获得较好的响应特性,而且参数的调整也比较困难,很难满足控制系统的高稳定性和强抗扰性的要求。而在整个主动磁悬浮控制统中,磁悬浮轴承的动态特性及转子的稳态精度和设计的控制器的好坏有直接的关系,因此,主动磁悬浮系统中的控制器的设计成了一个研究的热点问题。本文根据磁悬浮系统的非线性、参数不确定的特点,结合模糊控制和PID控制的特点,设计了模糊自适应PID控制器,来改善主动磁悬浮控制系统的控制精度和稳态特性。
1 主动磁悬浮控制系统模型
单自由度主动磁悬浮支承系统的原理图如图1所示,其结构采用差动的连接方式,单自由度主动磁悬浮控制系统由位移传感器、转子(悬浮体)、控制器、功率放大器和电磁铁五部分组成。转子的平衡位置为x0,当转子的实际位置发生偏移量x时,位移传感器检测到这一偏移信号并转换成相应的电信号Ux,Ux与转子平衡时的期望电压Ur进行比较,得到偏差信号Ue,进入控制器进行相应的运算,得到控制信号Uc,经过功率放大器输出控制电流信号,从而调节了电磁线圈中的电流的大小,改变了电磁铁产生的电磁力的大小,最终使得转子的位置减小偏移直至稳定悬浮。

图1 单自由度磁悬浮支承系统的结构图
在图1中,Ur为转子处于平衡位置时对应的输入电压值,Ux为转子实际位置所对应的电压值,Ue=Ur-Ux为偏差信号,Uc为模糊自适应PID控制器的输出信号,U0为上下两个电磁线圈的偏磁电流所需的电压值,I0为偏磁电流分量。
当质量为m的转轴在两个磁铁之间处于平衡时,假设忽略绕组漏磁、铁芯和转子中的磁阻及磁性材料的磁滞和涡流,那么上下两电磁铁产生的电磁力在转轴上的合力为零。当转轴偏离平衡位置时,偏离位移量为x,为了使转轴能回到原来的平衡位置,必须加一个控制电流i,使电磁铁I的磁力增加,电磁铁II的磁力减小。两个电磁铁产生的电磁力分别为:

式(1)中:μ0为气隙磁导率,μ0=4π×10-7H/m,S0为磁极气隙的截面积(m2),N为电磁铁线圈的匝数,I0为电磁线圈的偏置电流(A),x0是转子平衡时电磁铁与转子轴中心线之间的距离;x为转子偏离中心位置在该自由度上的位移(m),i为控制电流分量。F1和F2分别为两个电磁铁产生的电磁力。
作用在转子上的合力为:
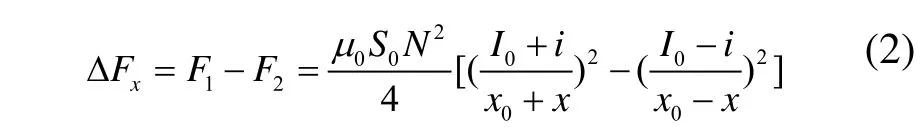
所以可以得到:

在转子平衡位置(即x=0, 0I= ),将式(1)展开成泰勒级数,并略去高阶小量,得:

对式(4)进行拉式变换,可以得到:

得到主动磁悬浮系统开环传递函数:
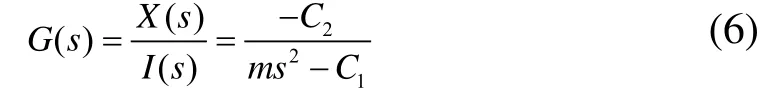
从式(6)可以看出,系统有两个极点,其中一个极点位于S平面的右半平面,造成开环控制系统不稳定。
2 模糊自适应PID控制器
2.1 模糊自适应PID控制器的组成
主动磁悬浮系统模糊控制器的设计如图2所示。

图2 主动磁悬浮模糊PID控制器
在图2中,R为给定转子平衡位置,Y为转子的实际位置,e为转子的位移偏差信号,de/dt为转子位置偏差的变化率,u为模糊自适应PID控制器的输出信号,即加在电磁铁线圈上的电压信号。当主动磁悬浮系统受到扰动影响时,使得转子偏离平衡位置,下降x时,即转子与电磁铁上线圈的距离偏大,位移传感器检测到转子此时的实际位置并转化为相应的电压信号,与转子平衡位置所对应的电压信号相比较,得到偏差信号e和偏差的变化率信号ec,这两个信号进入模糊控制器中,经过模糊化、模糊规则推理、模糊决策和解模糊化,在线整定PID控制器的三个参数Kp,Ki和Kd,使其达到最优化,经过PID控制器计算,得到控制信号增大,从而使得上线圈中的电流增大,下线圈中的电流减少,使得上线圈的电磁力F1增加,从而调节转子慢慢向上移动,直至转子回到平衡位置,实现转子的稳定悬浮。
普通的增量式PID控制算法为:

其中e(k)=r(k)-y(k),Kp、Ki和Kd为PID控制器的比例、积分和微分系数,模糊控制就是通过模糊推理在线整定Kp、Ki和Kd,送入PID控制器中进行计算得到控制信号u,从而调整线圈中的电流信号来实现转子的位置的调节。
2.2 模糊化和隶属度函数
从图2可以看出,模糊推理机构的输入信号为误差信号e和误差变化率ec,PID控制器的三个系数Kp、Ki和Kd为输出信号[3]。在转子偏离平衡位置较大时,实行大的控制量,粗调控制量,来增度系数;被称为主动磁悬浮系统的电流刚加系统调整的快速性;在转子偏离平衡位置较近时,实行细调控制量,来获得较好的稳态精度。因此选取输入输出变量e、ec的论域为{-3,-1.5,-0.5, 0, 0.5,1.5,3},Kp的论域为{-0.3,-0.2,-0.1, 0,0.1,0.2,0.3},Ki的论域为{-0.06,-0.04,-0.02, 0,0.02,0.04,0.06},Kd的论域为{-3,-2,-1, 0,1,2,3},对应的语言变量值分别定义为NB (负大)、NM (负中)、NS(负小)、ZO(零)、PS(正小)、PM (正中)、PB(正大)。e、ec、Kp、Ki和Kd的隶属度函数均采用三角波函数[4],如图3~图6所示。

图3 输入量e和ec的隶属度函数

图5 Ki的隶属度函数
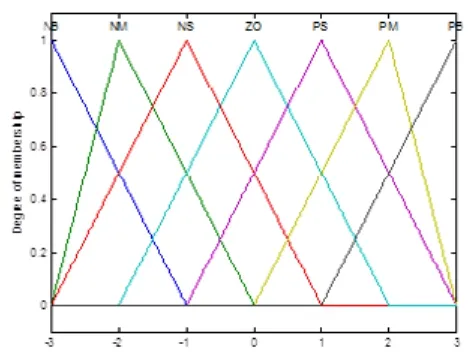
图6 Kd的隶属度函数
2.3 模糊推理
在主动磁悬浮模糊自适应PID控制器中,模糊控制器输出的三个参数Kp、Ki和Kd对系统的输出影响较大,比例系数Kp能减小转子与平衡位置的距离,加快转子回复到平衡位置的速度,Kp越大,主动磁悬浮的转子回复到平衡位置的速度越快,但是过大的Kp会使得磁悬浮系统变得不稳定;积分系数Ki可以消除转子实际位置与平衡位置之间的距离,Ki越大,转子和平衡位置之间的误差消除的就越快,但如果Ki过大,会产生积分饱和现象,使控制系统产生大的超调;Ki过小,使转子很难精确地回复到平衡位置,影响系统的控制精度。微分系数Kd可以改善系统的动态特性,但是Kd过大,会延长转子回复到平衡位置的时间,而且会降低系统的抗干扰性能。根据以上分析,同时考虑三个参数之间的相互影响,建立模糊推理语言规则。表1~表3分别为Kp、Ki和Kd的模糊控制规则。
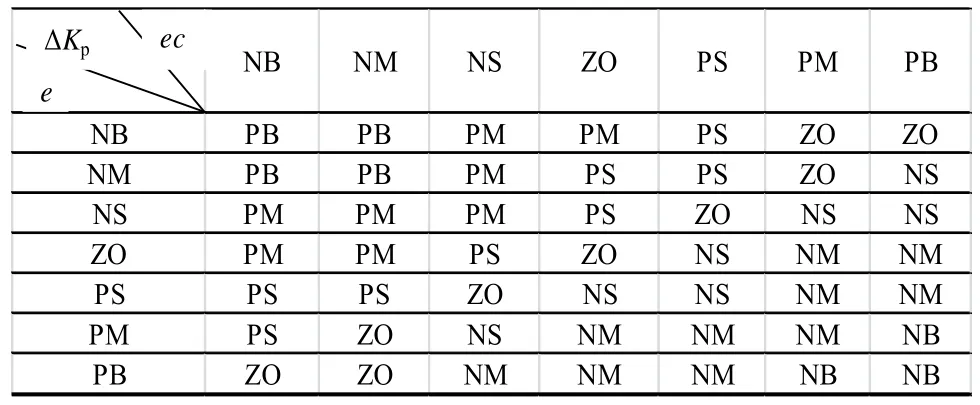
表1 Kd的模糊规则表

表2 Ki的模糊规则表

表3 Kd的模糊规则表
模糊控制器的输入输出之间的关系如图7所示。
2.4 解模糊化
采用工业控制中广泛使用的去模糊化方法-加权平均法[5],求得最终的△Kp、△Ki和△Kd,通过下面计算公式计算出Kp、Ki和Kd。
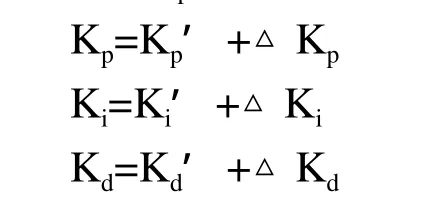

图7 模糊控制器的输入输出之间的关系
3 主动磁悬浮系统仿真及分析
在主动磁悬浮控制系统中,涉及的参数为:m= 12kg,x0=0.5×10-3m,I0= 3.0A,μ0= 4π×10-7Vs/Am,s0= 340mm2,N = 190,把这些参数代入到方程(6),可以得到主动磁悬浮控制系统开环传递函数为:
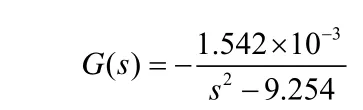
在MATLAB下进行编程仿真[6,7],当系统不存在扰动信号时,系统的输入信号为单位阶跃信号,系统的输出如图8所示,Kp、Ki和Kd的整定曲线如图9~图11所示。
模糊控制自适应PID控制器中的三个参数为:Kp= 0.41,Ki= 0.001,Kd= 0.31,可以看出,Kp在初始阶段,有大幅度的上升,用来加快系统的响应,此时Ki明显增大, 改善了系统稳态性能,系统慢慢趋于稳定,相应的Kd也明显加大,用来改善控制系统的动态性能,缩短调整时间。从输出曲线上来看,系统的超调量为2%,调节时间ts=0.13s,系统在t=0.2s时,输出能准确地跟踪输入信号,即经过0.2s,转子能准确回复到平衡位置。

图8 不加扰动时的系统输出

图9 Kp的整定曲线
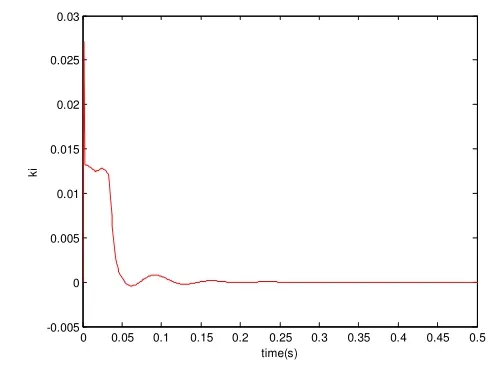
图10 Ki的整定曲线
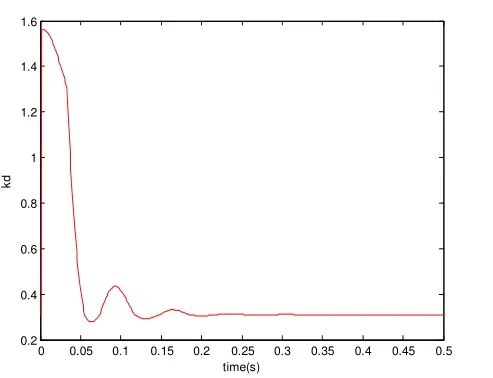
图11 Kd的整定曲线
在t = 0.4s时,给系统加一幅值为0.5的扰动信号,系统的输出如图12所示。
从图12可以看出,当系统受到扰动时,模糊控制器能迅速做出反应,并在线调整PID控制器的三个参数 Kp、Ki和Kd,使其达到最优,系统经过0.04s就可以抑制干扰信号的影响,使转子快速的回复到平衡位置。主动磁悬浮控制系统的抗干扰能力明显增强,系统具有较好的动静态特性。

图12 加入扰动后的系统输出
4 结束语
以主动磁悬浮控制系统为控制对象,根据主动磁悬浮系统的非线性、参数不确定等特点,针对普遍应用的PID控制器中参数难整定的问题,设计了模糊自适应PID控制器,并进行实时控制及结果分析。首先,对主动磁悬浮控制系统的结构及工作原理进行了介绍并建立了主动磁悬浮控制系统开环系统的模型;然后设计了模糊自适应PID控制器;最后,在模糊PID自适应控制器的实时控制下,对主动磁悬浮控制系统进行仿真和分析,设计的模糊自适应PID控制器能使得主动磁悬浮控制系统具有较好的动态特性和稳态特性。
[1] SHAM ELI E, KHAM ESEE M B,HU ISSOON J P.Nonlinear controller design for a magnetic levitation device[J].M icrosystem Technologies,2007,13(5):831- 835.
[2] 张小建.主动磁悬浮轴承数字控制系统的研究, 南京航空航天大学硕士论文,2002.
[3] 张静,徐林.磁悬浮系统的模糊自适应PID控制[J].计算机应用,2009,29(6):329-334.
[4] 诸静.模糊控制原理与应用 [M].北京:机械工业出版社,1995.
[5] 罗文广,韩俊峰,兰红莉.基于M atlab(Simulink)语言的模糊控制系统研究高级仿真[J].计算机仿真,2001,18(3):15-16.
[6] 刘金琨.先进PID控制及其Matlab仿真[M].北京:电子工业出版社,2003.
[7] 彭辉,徐锦华,侯海良.模糊控制在磁悬浮球系统实时控制中的应用[J].控制工程.2009,16(3):278-281.

