基于粒子群优化PIDNN的温室温湿度解耦控制仿真
洪运国
(大连职业技术学院 信息工程学院,大连 116035)
0 引言
多变量系统(M IMO)在控制过程中要求系统稳定性强,调节性能优良,能够以比较小的误差去跟踪设定值的变化。但是由于系统多个输入与多个输出之间具有某种程度的耦合作用,所以常常需对控制系统做解耦。传统的解耦控制是采取状态反馈把多变量系统化为完全解耦的线性系统,这种办法需要被控对象一定要运用准确的数学模型来表示。在农业工程中,温室大棚的温湿度控制就是一个多变量的控制系统,温室中的环境因子中温度和湿度是最基本的因子,其变化对农业作物影响最为显著。而且温湿度因子存在一定的耦合关系,对一个因子的控制常会影响另一个因子的变化,同时系统还具有非线性、大时滞的特点,很难建立精确的模型,采用传统的解耦控制很难达到系统的要求[1]。
PID神经元网络(pm po rlional—in teg ral—derivadve neural network),简称为PIDNN,是将PID控制规律融合进神经元网络之中,使神经元网络的隐含层单元分别具有比例、积分、微分功能,从而构成的一种新的前向多层神经元网络,存在非常好的自学习控制能力,能够在系统对象参数不明确的状况下经由自身的训练与学习得以完成多变量系统的解耦控制,使变量间的耦合消除,从而为多变量的强耦合系统解耦控制提供了一个新的途径[2]。
1 PID神经元网络
1.1 PID神经元网络结构

图1 PID神经元网络结构
PID神经元网络从结构上分为输入层、隐含层和输出层,网络结构为2—3—1,输入层有两个神经元,分别接收控制量的目标值 X1和当前值 X2,隐含层包含比例元P、积分元I和微分元D。输出层到隐含层的权值为ωij,隐含层到输出层的权值为ωjk,输出层为一个神经元。完成整个网络控制规律,多控制量神经元网络是多个单控制量网络的并联结构。
1.2 控制算法
1) 输入层
输入层包括2n个神经元,输出数据 xsi等于输入数据 Xsi,即 xsi( k ) = Xsi(k)。
2)隐含层
隐含层共3n个神经元,分别为n个比例神经元,n个积分神经元和n个微分神经元,输入值相同,输出为:

比例神经元输出:
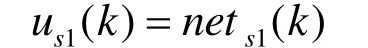
积分神经元输出:
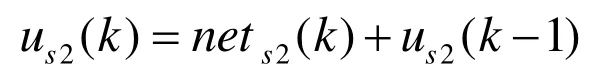
微分神经元输出
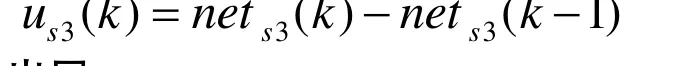
3)输出层
构成n维输出向量,是隐含层全部神经元的输出值加权和,公式如下:

其中s是并联网络的序号; j是网络中隐含层神经元的序号,ωij是网络输入层至隐含层的连接权值;h为输出神经元序号, usj(k)为隐含层神经元输出值;ωjk是隐含层至输出层的连接权值。
4)权值修正
PID神经元网络在控制过程中根据误差按照梯度修正法修正权值,使控制量不断接近控制目标。误差计算公式:
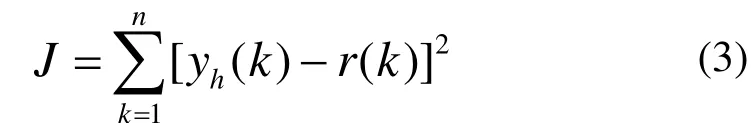
其中n为输出节点个数,yh为预测输出,r为控制目标。
5)PID神经元网络权值修正公式如下:
(1)输入层到隐含层:

(2)隐含层到输出层:
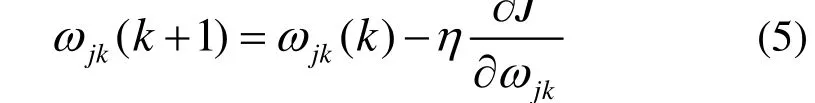
式中,η为学习速率。
2 温室温湿度耦合模型
温室温湿度控制系统是一个非线性、滞后的复杂的时变控制系统,系统在实施控制中温度控制能够引发湿度变化,同样湿度控制也能够引发温度变化。这种控制系统里湿度和温度之间的耦合关系如图2所示。
对被控对象采用一阶加纯滞后环节近似后可得到图中个环节的传递函数[3]。
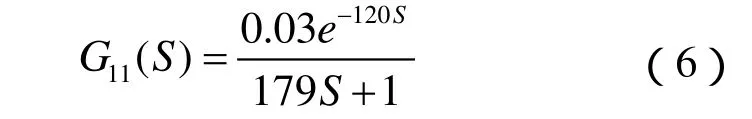

图2 系统对象传递函数框图
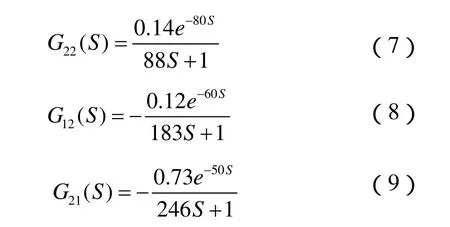
3 控制系统模型的建立
PID神经元网络控制器和温室系统构成的闭环控制系统如图3 所示。

图3 PID神经元网络闭环控制系统
其中1r, 2r是控制量的控制目标,即温度和相对湿度, 1u, 2u为控制器的控制律, 1y, 2y控制量的当前值。网络权值随机初始化,控制量的初始值为[0 0],控制目标为 [1 0.5],控制时间间隔为20m in,0.06η=。
4 仿真结果及其分析
PIDNN在进行训练和学习时,只是依据使目标函数为最小,调节网络连接权值,完成系统输入到输出的映射。因此只要训练样本中包括了解耦控制的要求,HDNN就可以按照学习算法逐步调整相应的权值,使系统解耦控制的性能达到最佳状态。
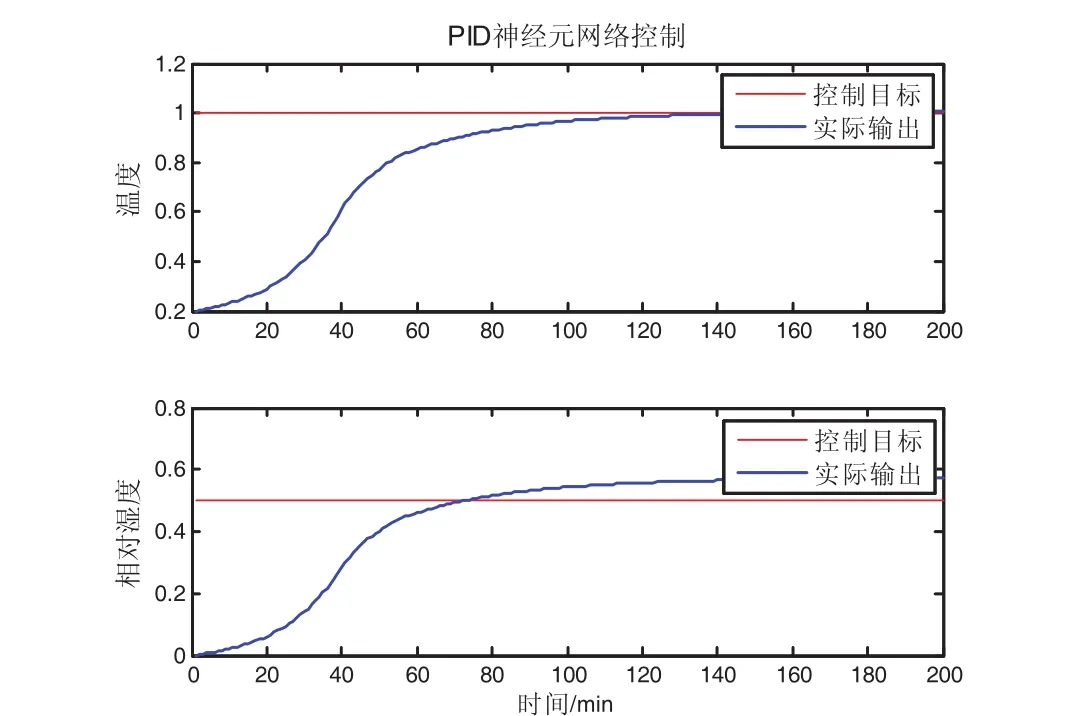
图4 PIDNN解耦控制效果
从图4可以看出,PID神经元网络控制器能够较好的控制温室系统中温度和湿度解耦控制,使控制量最终值接近目标值。
5 粒子群优化PIDNN解耦控制
PID神经元网络采用的是梯度学习方法,初始权值随机得到,权值在学习过程中为避免陷入局部最优,可采用粒子群算法优化神经元网络得初始权值。
采用均方误差函数做适应度函数和粒子群算法两者结合以后,PIDNN的权值调整改变为采用粒子在整个解空间范围内搜索全局最优位置当作网络权值,权值更替为粒子速度与位置的更新,而不再运用传统的误差反传算法[4]。
将PIDNN网络中输入层到中间层权值ijω取(-1,+1)之间一个定值,即它的权值不再运用粒子群迭代公式作更新,来降低网络训练中的循环次数与计算量。中间层到输出层的权值当作粒子群的寻优参数,系统训练步骤遵照以下各步进行:
1)PINDD各层的连接权值做初始化,让粒子位置和中间层到输出层的权值做到对应,对初始粒子位置iX和速度iV赋予随机值。
2)根据适应度函数计算粒子的适应度值,以确定个体极值iP和群体极值gP。
3)开始循环迭代,按照下面公式[5]更新粒子的位置iX和速度iV。

ω为惯性权重, k为当前迭代次数, c1和 c2为加速度因子, r1和 r2为分布[0,1]之间的随机数。 d = 1 ,2,3… ,D 表示D维搜索空间。
4)以更新粒子的位置iX赋给PIDNN相应的权值,计算网络输出,并回至第2)步,进行再一次迭代,一直到达设定的循环次数,最终得到网络的最优权值。
PIDNN和粒子群算法相结合,把粒子位置和神经网络权值对应起来,采用粒子在权值空间里搜索最优位置,让其适应值函数获得全局极小值,防止神经网络算法的局部收敛和对初值依赖的缺陷[6,7]。仿真结果如图5所示,系统的响应速度加快,而超调量减小。
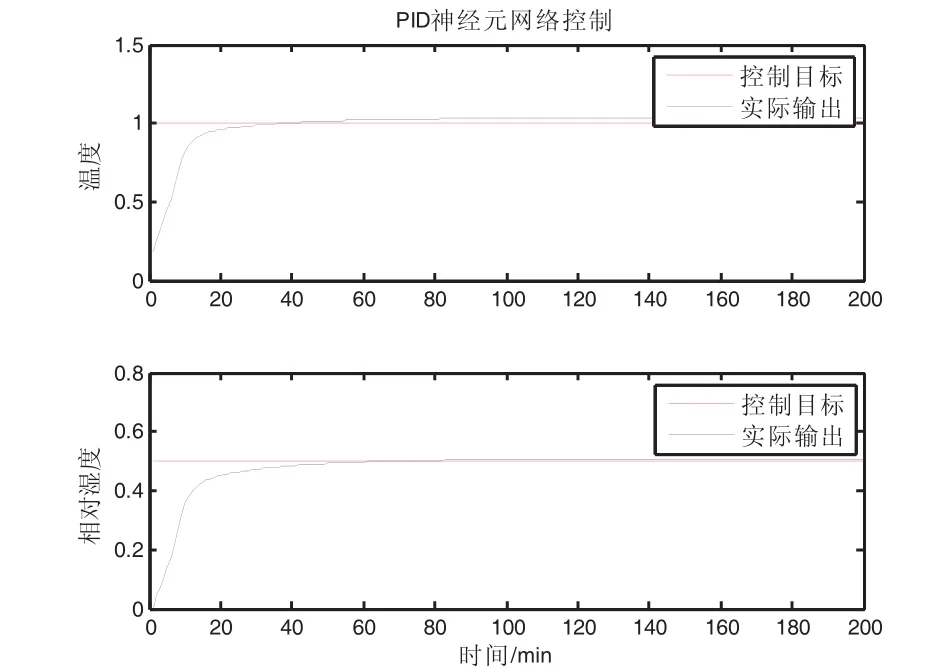
图5 粒子群优化PIDNN解耦控制
6 结论
仿真结果验证了利用粒子群搜索PIDNN最优权值是一种较好的优化手段,训练后的PIDNN解耦控制器调节时间明显减小,对其相应的设定值具有较好的跟随性,减小了温、湿度控制回路之间的干扰,增强了控制系统的鲁棒性,是一种有效地解耦控制方法。
[1] 宫赤坤,毛罕平.温室温湿度遗传模糊神经网络控制仿真研究[J].江苏理工大学学报(自然科学版).2000,21(6):35-37.
[2] 舒怀林,郭秀才.多变量强耦合时变系统的PID神经网络控制[J].工矿自动化,2003(5):16-18.
[3] 马利英,任庆昌,李建维.温湿度解耦在变露点控制中的应用研究[J]. 建筑热能通风,2008,27(6):40-43.
[4] 梁军,程灿.改进的粒子群算法[J].计算机工程与设计,2008,29(11):293-296.
[5] 杨朝霞,方建文.粒子群优化算法在多参数拟合中的作用[J].浙江师范大学学报,2008,31(2):173-177.
[6] 张选平,秦国强.一种动态改变惯性权的自适应粒子群算法[J].西安交通大学学报,2005,39(10):1039-1042.
[7] 吕振肃,侯志荣.自适应变异的粒子群优化算法[J],电子学报,2004,32(3):416-420.

