乏油润滑直齿轮传动瞬态温度场主要影响因素分析

丁有永，朱如鹏，李政民卿

（南京航空航天大学机电学院，江苏南京 210016）

齿轮接触表面的摩擦热流密度由接触应力、齿面的相对滑动速度和齿面摩擦系数确定，其计算公式［8］为:

0 引言

在很多实际工程应用润滑中，常常会出现润滑油供应不足，即乏油的情况，严重的乏油将会使得齿轮传动失效［1］。闫玉涛等［1～2］开展了锥齿轮乏油润滑下稳态本体温度场研究。王延忠等人对航空螺旋锥齿轮润滑过程进行了分析，理论分析了轮齿表面的温度变化［3］。龙慧等人对高速齿轮的温度场进行了模拟，对降低轮齿温度提出了一些方法［4］。目前，针对乏油润滑直齿轮传动的瞬态温度场研究较少。

本文利用摩擦学、传热学、赫兹接触等理论，给出了乏油润滑直齿轮齿面摩擦系数、轮齿不同啮合位置的摩擦热流密度以及轮齿端面、轮齿齿面等区域的对流换热系数的计算方法;建立了轮齿本体温度场有限元分析模型，获得了齿轮轮齿的稳态温度场和瞬态温度场分布，分析了润滑油粘度、齿宽、载荷和转速对瞬态温度场的影响。

1 乏油润滑轮齿瞬态温度场主要参数计算方法

1.1 乏油润滑齿面摩擦系数计算方法

计算乏油润滑状态下齿面摩擦系数的一种方法认为:乏油润滑摩擦系数uf由边界润滑状态下的摩擦系数ub与弹流润滑摩擦系数uc共同决定的［5］，可以表示为:

式中，kc为弹流油膜的承载系数;kb为峰点接触的承载系数，且kc+kb=1。

润滑良好的情况下齿面摩擦系数的计算公式为［6］:

式中，Ftc为轮齿啮合点的切向载荷，b为轮齿啮合点处的齿宽，XR为齿面粗糙度因子，η为润滑油的动力粘度，v1、v2分别为主、从动轮在啮合点的速度。

边界润滑下线接触齿面的摩擦系数计算公式为［7］:

式中，w为单位齿宽载荷，E为综合弹性模量，RE为综合曲率半径。

将式（1）、式（2）和式（3）联立，即可得到乏油润滑齿面摩擦系数。

1.2乏油润滑齿面摩擦热流密度计算方法

齿轮接触表面的摩擦热流密度由接触应力、齿面的相对滑动速度和齿面摩擦系数确定，其计算公式［8］为:

式中，q1c为摩擦热流密度，β为热量分配系数，γ为热能转换系数，uf为乏油润滑齿面摩擦系数，pnc为啮合点赫兹接触应力，vs为啮合点相对滑动速度。

啮合过程中，当轮齿旋转一周，在齿面各啮合处都有一次瞬时摩擦热流密度的输入。假定在啮合处的赫兹接触区宽度为2a，则主动轮轮齿接触区摩擦热流密度通过此宽度的时间t1c为:

式中，a为轮齿赫兹接触半宽，v1c为主动轮在啮合点处的速度。

主动轮每旋转一周所需时间t1为:

式中，n1为小齿轮转速。

因此，主动轮每旋转一周期，其轮齿在相应啮合位置获得的平均摩擦热流密度q1ca为:

将式（4）、式（5）、式（6）代入式（7）中，即可得到平均摩擦热流密度。

1.3 乏油润滑轮齿表面对流换热系数计算方法

乏油润滑齿轮对流换热介质为润滑油和空气的混合物，在计算中，将两者混合体的热物性参数带入计算［9］。混合体的热物性参数近似表示为:

式中，ρ为混合体的密度，c为混合体的比热容，η为混合体动力粘度，λ为混合体导热率，带下标“o”和“a”的分别为单向流动状态下的润滑油和空气的上述热物性参数，d为空气和润滑油的比例系数［10］。

啮合齿面对流换热系数可由下式计算:

式中，n为齿轮转速，r为齿轮分度圆半径，ρ为混合体的密度，η为混合体动力粘度，c为混合体比热容，λ为混合体导热率，L为轮齿分度圆直径。

将式（8）带入式（9）中，即可得到乏油润滑齿面对流换热系数。

端面对流换热系数可由下式计算:

将式（8）带入式（10）中，即可得到乏油润滑端面对流换热系数。

2 乏油润滑轮齿瞬态温度场主要影响因素分析

2.1 乏油润滑轮齿瞬态温度场模拟

在齿轮每转一周的过程中，各个轮齿所经历的过程是完全相同的。因此，在研究齿轮温度场时，通常取单个轮齿来进行研究［6］。本文取单个轮齿进行分析，所用齿轮参数、载荷及转速如表1所示，传热介质的热物性参数如表2所示。

表1 算例齿轮传动特征参数

表2 传热介质的热物性参数

利用本文1.2节方法得出的齿面摩擦热流密度作为热载荷加载在啮合齿面的表面效应单元上;利用本文1.3节方法得出的对流换热系数作为对流载荷加载在轮齿的各个面上，可进行随后的齿面温度场分析。

齿轮瞬态温度场是基于稳态温度场的基础上进行的，因此，先要得出齿轮的稳态温度场。根据表1和表2的参数算出齿面加载的摩擦热流密度和对流换热系数，然后将平均摩擦热流密度加载在啮合齿面上，将对流换热系数作为对流载荷加载在轮齿的各个面上，得出乏油齿轮传动的轮齿稳态温度场，如图1所示。

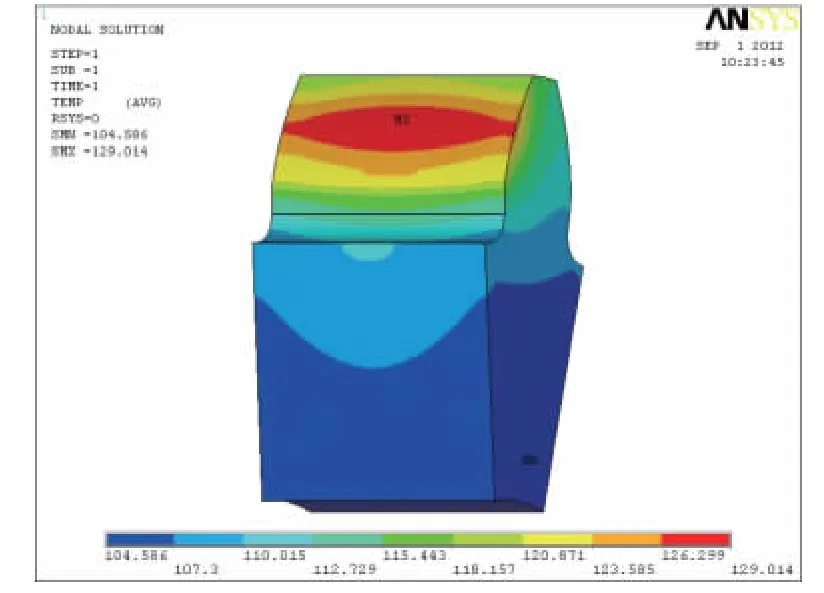
图1 乏油润滑轮齿稳态温度场分布等值线图

根据图1可知，轮齿工作齿面的温度明显高于轮齿的本体温度，热传导使温度由齿面到齿体呈一定梯度分布形式;齿面温度沿齿宽方向是对称分布，由于端面对流换热导致轮齿端面的温度明显低于轮齿中部温度;稳态齿面最高温度出现在齿面节点偏向齿顶位置。

在稳态温度场基础上，计算出各个啮合点的时间，应用载荷步将瞬时摩擦热流密度模拟出移动热源加载在啮合齿面的各个节点上，得出乏油润滑轮齿瞬态温度场，如图2所示。

图2 乏油润滑轮齿瞬态温度场分布等值线图

根据图2可知，由于瞬时摩擦热流密度输入时间极短，轮齿齿面啮合位置大幅升温，但齿体温度基本保持不变;齿面瞬时最高温度出现在靠近齿根位置;在轮齿节圆附近也有一个峰值，与稳态温度最大值的位置相吻合。

2.2 瞬态温度场主要影响因素分析

a）润滑油动力粘度的影响分析

润滑油动力粘度对乏油润滑齿面的摩擦系数和对流换热系数都有重要的影响，粘度越大，齿面的摩擦系数越小，产生的摩擦热流量也就要小，但是散热效果较差，因此润滑油动力粘度对乏油润滑瞬态温度场的影响是个复杂的过程，有必要进行分析。分析中，沿轮齿啮合面中部径向方向选取各个节点，在其他条件不变的情况下，得出同润滑油动力粘度瞬时接触齿面温度的分布规律如图3所示。

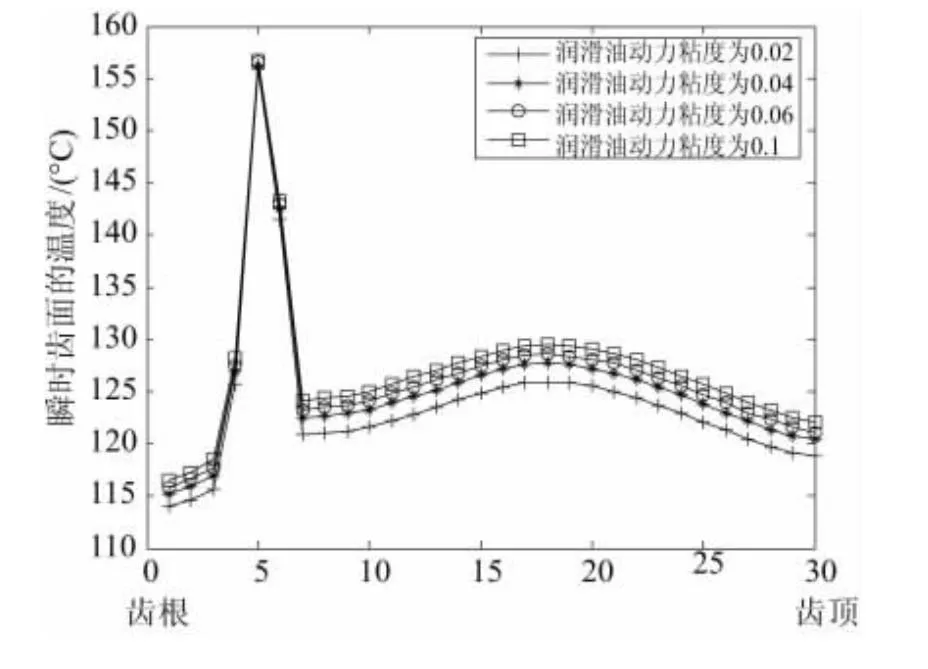
图3 润滑油动力粘度对瞬时接触齿面温度的影响

根据图3可知，在不同润滑油动力粘度下齿面的瞬时温度分布规律是一致的，但随着润滑油粘度的增加，齿面瞬时温度的增加很小，特别是在靠近齿根处的最大瞬时温度位置，瞬时温度几乎没有变化。主要原因是:在稳态时，由于粘度增加，齿面摩擦热流密度减小，但是对流换热系数也减小，导致稳态温度有一定的升高，在计算瞬态温度场是主要考虑瞬时摩擦热流密度的影响，瞬时温升最大值有一定的降低，将两者叠加，就出现上面的情况。因此，润滑油粘度对乏油润滑瞬态温度场影响很小;但在满足其他条件的情况下，如尽量取较小值，则可以在一定程度上降低齿面瞬时温度。

b）齿轮齿宽的影响分析

轮齿齿宽对乏油润滑齿面摩擦热流密度有很重要的影响，随着齿宽的增大而减小，但是齿宽的增大却不利于轮齿的散热。分析中，沿轮齿啮合面中部径向方向选取各个节点，在其他条件不变的情况下，得出不同齿宽瞬时接触齿面温度的分布规律如图4所示。

图4 齿宽对瞬时接触齿面温度的影响

根据图4可知，在不同齿宽下齿面的瞬时温度分布规律是一致的，齿宽为14mm时的瞬时齿面温度是最高的，但随着齿宽的增加，瞬时接触齿面的温度降低，这主要是因为齿宽增大，轮齿所受的单位载荷变小，最终导致的温度降低的影响大于对流换热的影响。因此，减小齿宽不能降低齿面瞬时温度，故在满足质量等要求的情况下，应尽量选择较大齿宽。

c）载荷的影响分析

载荷对乏油润滑齿面摩擦热流密度有着很重要的影响。由有限元分析知道，由于在不同载荷下，乏油润滑齿面的瞬时温度分布规律是一致的。因此在其他条件不变，只改变载荷的情况下，选取啮合瞬时齿面最大温度的变化趋势作为轮齿瞬时温度场的变化趋势。轮齿齿面瞬时接触最大温度随载荷变化的趋势如图5所示。

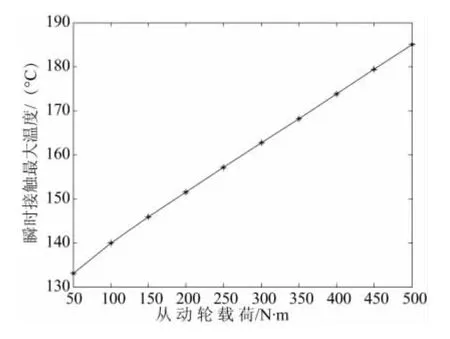
图5 载荷对齿面瞬时接触最大温度的影响

根据图5可知，瞬时接触齿面最大温度随着载荷的提高一直增加，基本呈线性增长。因此，载荷对轮齿瞬时温度场的影响非常大。

d）转速的影响分析

转速对乏油润滑齿面摩擦热流密度和齿面对流换热系数有着很重要的影响，故转速也是影响乏油润滑齿轮瞬态温度场的重要因素。分析中，沿轮齿啮合面中部径向方向选取各个节点，在其他条件不变的情况下，得出不同转速瞬时接触齿面温度的分布规律如图6所示。

图6 转速对瞬时接触齿面温度的影响

根据图6可知，随着主动轮转速的增大，瞬时齿面的温度升高，但温度最大值的增加却趋于平缓，其主要原因为当转速较大时，齿面摩擦系数会减小，导致齿面摩擦热流量的增加量降低，最终影响温度增加的趋势;瞬时温度在齿面上的分布不一致，当转速较小时，节圆附近靠近齿顶处的温度分布较均匀，随着转速的增大，该位置的温度分布不再均匀，出现明显的极值点。

3 结语

通过对乏油润滑直齿轮传动瞬态温度场的模拟以及润滑油粘度、齿宽、载荷和转速对其影响的分析，得出以下结论:

1）轮齿稳态最高温度出现在节圆偏向齿顶部分，但齿面瞬时最高温度则出现在靠近齿根位置;

2）润滑油粘度对乏油润滑瞬态温度场影响很小，但在满足其他条件的情况下，如尽量取较小值，则可以在一定程度上降低齿面瞬时温度;

3）减小齿宽不能降低齿面瞬时温度，故在满足质量等要求的情况下，应尽量选择较大齿宽;

4）载荷对轮齿瞬时温度场的影响较大，且瞬时接触齿面最大温度随着载荷的提高呈线性增加;

5）随主动轮转速增加，齿面瞬时温度升高，但温度最大值增加则趋于平缓，且齿面上瞬时温度分布不一致。

［1］闫玉涛.航空螺旋锥齿轮失油状态下生存能力预测方法的研究［D］.沈阳:东北大学，2009.

［2］王伟.弧齿锥齿轮的本体温度场的有限元分析［M］.湘潭:湖南科技大学，2009.

［3］王延忠.王涛.周元子.高航空螺旋锥齿轮乏油润滑过程分析［J］.润滑与密封，2008，33（10）:209-216.

［4］龙慧.高速齿轮传动轮齿的温度模拟及过程参数的敏感性分析［D］.重庆:重庆大学，2001.

［5］王慰祖，黄平.点接触边界润滑吸附膜计算模型［J］.摩擦学学报，2008，28（3）:240-243.

［6］龚宪生，王欢欢，张干清.行星齿轮轮齿本体温度场与闪温研究［J］. 农业机械学报，2011，42（10）:209-216.

［7］温诗铸，黄平.摩擦学原理［M］.北京:清华大学出版社，2008.

［8］章易程.齿轮乏油传动的摩擦学设计［D］.长沙:中南大学，2011.

［9］邱良恒，辛一行，王统，等.齿轮本体温度场和热变形修形计算［J］.上海交通大学学报，1995，29（2）:79-86.

［10］N.Patir.“Estimate of the Bulk Temperature in Spur Gears Based on Finite Element Temperature Analysis”.［M］.Northwestern University，USA.1976.