基于免疫算法的非等间隔梳状谱信号峰均功率比抑制研究

吕大鑫，傅石雨

（1.通信信息控制和安全技术重点试验室，嘉兴314033；2.中国电子科技集团公司第36研究所，嘉兴314033）

0 引 言

峰均功率比（PAPR）随载波数目增大而升高是多载波信号的固有缺陷，高的峰均比使功率放大器处于非线性工作区，降低了发射系统性能。作为提高发射系统输出信号功率、工作效率和信号杂散指标的一个重要突破口，抑制峰均比的研究一直是通信界关注的焦点。目前广泛研究的是正交频率差异多路技术（OFDM）等载有调制信息的、具有等频率间隔特征的信号，也得到一些有效抑制PAPR的办法。但对非等频率间隔的梳状谱信号研究甚少，目前也没有十分有效的算法。以对抗联合战术信息分发系统（JTIDS）采用的非等间隔梳状谱信号为例，它具有非等频率间隔、固定频率集的特点，很值得采用一种多目标优化算法对其进行特定的优化，降低PAPR，提高干扰信号的发射功率和干扰效果。近年来，人工智能在自适应信号处理领域受到关注，其中免疫算法给了我们在非等间隔梳状谱信号峰均比抑制方面一些启示。

免疫算法作为一种新兴的仿生算法，具有并行处理、智能度高、全局搜索、收敛性好、鲁棒性好等特点，在解决大空间、非线性、全局搜索、多目标优化等复杂问题上具有独特的优越性。抑制信号峰均比的方法中，对信号无损的方法是优化各个子载波的初始相位。JTIDS信号的载频共51个，问题可以归结为已知一组频率集，求一组优化初始相位，使合成非等间隔梳状谱干扰信号的峰均功率比最小。

1 非等间隔梳状谱信号模型

JTIDS的数据链所采用的51个跳变频率点分布在969～1 008MHz、1 053～1 065MHz和1 113～1 206MHz 3个频段范围内，跳频点以3MHz为间隔均匀分布，频率跳变周期与脉冲周期相同，相邻脉冲的载频最小间隔是30MHz。针对JTIDS的非等间隔梳状谱干扰信号模型：

式中：fi为上述51个频率；θi为各子载波的初始相位。

产生的梳状谱干扰信号频谱如图1所示。

图1 对JTIDS非等间隔梳状谱干扰信号频谱

如果各子载波的初始相位全为零，即不对非等间隔梳状谱信号的初始相位优化，其峰均功率比将达到17dB（文中的PAPR为低通信号定义，即正弦波的PAPR为0dB），如此高的峰均功率比使得功率放大器的发射功率和效率极低。从图2可以看出，非等间隔梳状谱信号时域波形中的峰值非常高，信号包络变化十分剧烈，没有经过相位优化的非等间隔梳状谱信号是不能使用的，这样的信号波形甚至会损伤功放。

2 免疫算法相位优化

2.1 3种经典相位优化法

图2 全零初始相位非等间隔梳状谱信号波形图

对于频率间隔相等的梳状谱信号，可以通过解析代数式的方法获得优化的初始相位。频率间隔相等的梳状谱信号表达式为：

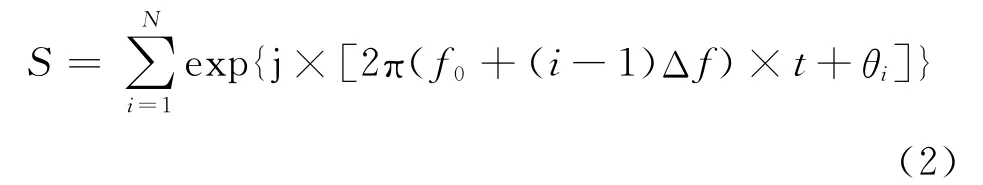
式中：f0为中心频率；Δf为频率间隔；θi为各子载波的初始相位。

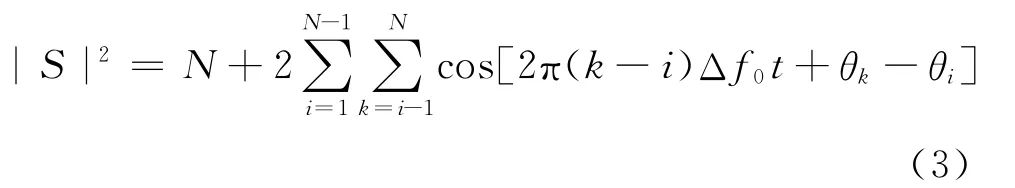
该信号的瞬时功率为：若想获得最小的PAPR，就是要求信号瞬时功率的峰值最小，即求解：

下面是国外3位学者给出的近似解［1］：

Newman相位［2］：1965年 D.J.Newman给出了求解式（4）的近似二次解：

Narahashi相 位［3］：1994 年，S.Narahashi和Nojima给出了求解式（4）的另一种近似二次解：

Pintelon相位：R.Pintelon和J.Schoukens在2001年其专著中给出了另一种新的近似二次解：

这3种针对频率间隔相等的梳状谱信号的相位优化方法，也可以在非等间隔频率集的梳状谱信号上使用，对峰均功率比抑制有一定的效果，但效果并非最优。图3为采用Narahashi法相位优化得到的51频点非等间隔梳状谱干扰信号波形图。该信号的峰均功率比PAPR为3.64dB，从波形图可以看出信号的幅度均匀，包络除了存在小幅波动外基本恒定，但还是有进一步优化的空间。

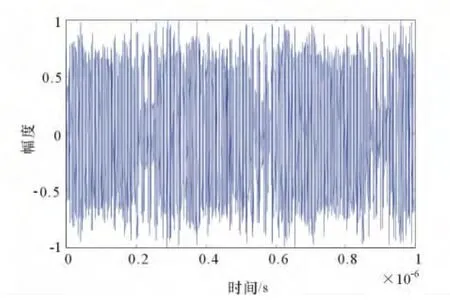
图3 Narahashi相位优化51频点非等间隔梳状谱信号波形图

2.2 免疫算法计算流程

免疫系统是一种并行的智能自适应学习系统，能自动识别并清除抗原，实现机体免疫防卫功能。免疫系统的识别、学习、记忆、自适应等特性使人工智能应用在工程领域得到了启示。现在广泛应用于工程领域的免疫算法，其理论基础是Burnet的基于生物抗体的克隆选择学说、Jerne的免疫网络学说和反向选择机制。免疫算法把要解决的问题和约束条件当作抗原，把问题的解当作抗体，通过免疫操作使抗体在解空间不断搜索进化，按照亲合度对抗体与抗原之间的匹配程度以及抗体之间的相似程度进行评价，直至产生最优解［4］。

采用免疫算法优化非等间隔梳状谱信号的初始相位时，梳状谱信号的频率集是给定的，通过寻找最优初始相位组合，不断优化合成的非等间隔梳状谱信号，尽可能降低合成信号的峰均功率比。免疫算法中的抗原对应期望非等间隔梳状谱干扰信号，抗体对应初始相位集合，亲和度是衡量优化程度的指标，这里亲和度对应峰均功率比的倒数，亲和度越高代表峰均功率比越低。这样，初始相位集合的寻优过程向着亲和度增大的方向进行。

免疫算法的计算流程如图4所示，初始抗体群体由Narahashi相位法生成，以获得具有较高亲和度的搜索起点，减少迭代次数。

图4 免疫算法计算流程图

图5为免疫算法优化初始相位集合的收敛曲线，迭代300次左右，峰均功率比即可减小到2.9dB以下，这个结果比Narahashi相位优化后的3.64dB低0.7dB，在峰均功率比已经比较低的情况下，0.7dB的优化非常可观。

图5 免疫算法的收敛曲线

由免疫算法优化得到的初始相位集合生成的51个频点非等间隔梳状谱信号波形如图6所示。因为算法流程中采用的初始抗体群为Narahashi相位法生成的，所以该波形图还有图3的大部分特征，但是经过免疫算法优化后，该非等间隔梳状谱信号的幅度更加均匀，包络的波动减小，这反映在峰均功率比方面就是PAPR进一步降低至2.88dB。

3 结 论

目前应用较多的相位优化算法有解析代数式算法、搜索算法以及循环查找法。解析代数式法只局限于等频率间隔的梳状谱信号，循环查找等基本的搜索法易产生“局部收敛”。当遇到采用单一的一种算法难以得到最优结果的情况时，可以考虑算法级联，如：先采用解析代数式法，再循环查找，最后采用免疫算法做“终极优化”。

图6 免疫算法优化后51频点非等间隔梳状谱信号波形图

基于免疫算法的相位优化方法突破非等间隔梳状谱信号的频率间隔和频点数目限制，更具有通用性，并可在其它算法优化的结果上取得更佳效果。

［1］江涛.OFDM无线通信系统中峰均功率比的研究［D］.武汉：华中科技大学，2004.

［2］Boyd S.Multitone signals with low crest factor［J］.IEEE Transactions on Circuits and Systems，1986，CAS－33（10）：1018－1022.

［3］Narahashi S，Nojima T.New phasing scheme of N－multiple carriers for reducing peak－to－average power ratio［J］.Electronics Letters，1994，30（17）：1382－1383.

［4］叶剑锋，王玉峰.基于免疫算法的相位控制方向图零点生成［J］.现代雷达，2007，29（12）：65－68.