考虑量测冗余度的多阶段PMU优化配置

吴 霜，卫志农，孙国强，郑玉平

(1.河海大学可再生能源发电技术教育部工程研究中心，江苏南京 211100;2.国网电力科学研究院，江苏南京 210003)

相量测量单元(phasor measurement unit，PMU)是广域测量系统的重要组成部分，已在电力系统的实时分析和监控［1-3］中得到应用。目前，PMU优化配置［4-6］工作主要集中在满足全局可观测或N-1故障情况可观测条件下减少的PMU数量，且大部分文献考虑的都是在系统中一步到位配置所有的PMU。实际上，由于PMU价格昂贵，系统难以一次性安装全部所需的PMU，且电力系统网架也处于改造升级的多阶段动态发展中，现有的PMU配置有可能会出现由于网络拓扑结构发生改变而导致一些节点或线路不可测的情况出现。

笔者综合考虑多阶段和N-1故障情况，首次提出考虑量测冗余度的多阶段PMU优化配置。为说明问题，将优化配置过程分成2个阶段，系统在第1阶段满足全局可观测，第2阶段满足N-1故障情况下可观测。相较于PMU，电力系统中线路发生故障的可能性更大，故本文只考虑失去一条线路的N-1故障情况。

1 电力系统可观测性

1.1 节点和系统的可观测分析

电力系统中，称电压相量可测量或可求出的节点为可观测节点;反之为不可观测节点［7］。根据以上定义，可得出如下规则:(a)已经配置了PMU的母线节点i，其节点电压相量可被直接测量，于是节点i可观测。(b)若支路一端的母线节点i装有PMU，则该节点的电压相量和与该节点相连所有支路的电流相量也可被直接测量。根据欧姆定律，能够计算出节点i邻接节点的电压相量，于是节点i的邻接节点也可观测。(c)若节点i为零注入节点，其邻接节点个数为k，根据欧姆定律和基尔霍夫定律，这k+1个节点只要k个可观测，就可计算剩下节点的电压相量，于是k+1个节点均可观测。

基于上述讨论，可以认为对一个有n个节点的系统，若n个节点均可观测，就称该系统是可观测的。

1.2 系统量测冗余度

一般来说，系统不仅要求可观测，同时也要求有一定的量测冗余度。由于本文不考虑PMU故障，即安装了PMU的系统节点一定可观测，因而这些节点量测冗余度记为1。根据上文节点的可观测分析，在已知线路阻抗的前提下，可以求得系统中各个节点i电压被直接或间接测量的次数，并取此测量次数为该节点的量测冗余度Ri。系统量测冗余度R由所有节点的量测冗余度相加得到，即

以图1的7节点系统为例，设节点1，2，7配置了PMU，故其节点量测冗余度均为1。再查找与安装PMU节点直接相连的节点，得{3(2)，4(1)，6(7)}，其中，3(2)表示节点 3 通过与安装PMU的节点2相连，被观测1次。再查找与零功率注入节点相连接的节点是否可以被观测，得{5(4)，5(6)}。虽然此时节点1，3，5电压都已知，但节点4却不能通过KCL定律判断又被观测1次，因为之前节点5的电压是通过节点4计算得出，不能逆向推导。至此，图1中所有节点的观测次数已不能再增加，节点1 ～7的量测冗余度为 1，1，1，1，2，1，1，此时系统量测冗余度为 8。

图1 计算节点量测冗余度Fig.1 Calculation of node redundancy

2 多阶段PMU优化配置分析

2.1 多阶段PMU优化配置的求解思路

由于经济和技术条件的限制，加上电力系统网架处于多阶段的动态发展中，系统中PMU配置不可避免地需要分多个阶段安装，所以有必要对多阶段PMU优化配置进行研究。不少文献［8－10］在研究多阶段PMU优化配置时，将满足全局可观测的配置方案作为最后一个阶段的目标。但是，由于线路故障会导致一些节点或线路不可测，这就需要考虑N－1故障情况下PMU的配置。因此本文最后一个阶段考虑系统满足N－1故障情况下可观测。

一个N节点的系统，根据实际经济和技术能力，决定分成t个阶段来完成PMU的安装。每一阶段需满足系统完全可观测，最后一个阶段满足N－1故障情况下可观测。除了满足系统可观测约束外，多阶段PMU配置还需满足以下约束:每一阶段的解必须包含上一阶段的解。例如用Si表示多阶段PMU配置在第i阶段的解，则有 Si⊃Si－1(i=2，3，…，t)，这样，每一阶段实际需要配置的解集=Si－ Si－1。

令xi为N维二进制变量，xi=1表示节点i安装了PMU;反之未安装。假设从节点集合S中选取节点安装PMU，即S中的节点xi=1，不在集合S中的节点xi=0。令ni(i=1，…，t)表示每一阶段安装PMU的个数，则有

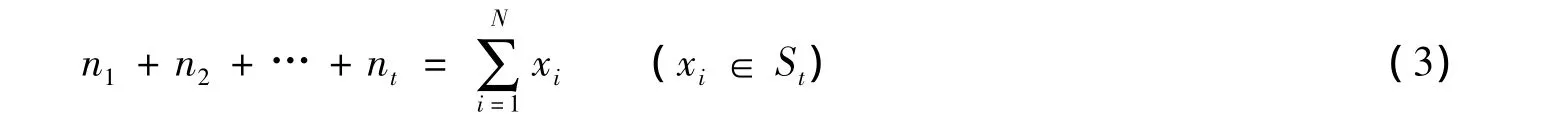
2.2 PMU配置模型

设PMU分2个阶段进行配置，该配置问题可描述为满足一定约束条件的单目标极小化问题，即

式中Ω为满足约束条件的可行解集合。

对于第1阶段，约束条件为

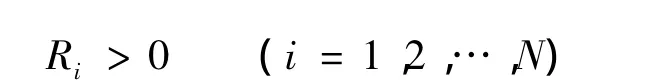
在此阶段，系统需满足全局可观测。

对于第2阶段，约束条件为

可以看到，第2阶段的约束条件除了要满足系统N－1故障情况下可观测外，其PMU的配置还需包括第1阶段的解。实际上，在这一阶段，并不要求所有节点的量测冗余度都大于1。考虑冗余度为1，以及冗余度为2且零功率注入节点。如果失去连接这2种节点的线路，前一种节点会变成孤立节点，后一种节点无功率流过，所以没有必要保证这2种节点在N－1故障情况下可观测，即不要求这些节点的量测冗余度大于1。同样安装PMU节点的量测冗余度也不要求大于1，这样可以进一步减少PMU的配置个数。

3 具体实现

3.1 改进遗传禁忌搜索算法

遗传算法(GA)是一种模仿自然界生物优胜劣汰、适者生存机理的优化算法。而TS算法［11－12］是局部领域搜索算法的推广，其特点是采用了禁忌技术。遗传禁忌搜索算法综合了GA并行大范围搜索的特点和TS的局部搜索能力，在算法的全局收敛性能和避免局部极小方面有明显改善。将遗传禁忌搜索算法直接运用于PMU优化配置中，总会出现不可行解。本文应用遗传禁忌搜索算法，将不可行解反映到算法的适应度函数中，具体是将GA的适应度函数和TS算法的评价函数都设为NPMU+NR=0，NR=0表示系统中量测冗余度等于零。这样遗传禁忌搜索算法能自动辨识不可行解并降低适应度值，再进行不可行解的修复，以确保每代遗传禁忌搜索算法的解都是可行解。将改进遗传禁忌搜索算法应用于PMU优化配置中，能快速得到比较好的优化配置结果。

3.2 多阶段优化配置的设计

a.设定初始参数，包括GA中群体规模m、最大迭代次数K以及TS算法中禁忌表长度L等。

b.编码。二进制编码，采用1个索引表IP和1个相邻点表P2［13］来存储系统网络图，压缩数据的存储空间，有效地降低了算法耗时。

c.首先需计算出第1阶段满足全局可观测的解S1。应用GA对个体进行选择、交叉、变异等运算。每进行10次GA，调用1次TS算法，对群体中的每个个体进行局部搜索，改进群体点的质量。

d.对系统进行可观测性分析及修复不可行解。

e.运用精英保留策略对群体进行处理。精英保留策略是为了解决由于随机因素导致优化过程中优秀个体丢失的问题。算法开始时随机产生一个初始群体P0，在此基础上采用二元锦标赛选择、交叉、变异操作，产生一个新群体Q0，P0和Q0的群体规模均为m。将Pt和Qt并入到Rt中(初始时t=0)，并按适应度由高到低进行排序，从中依次选取个体进入Pt+1，直到Pt+1的规模为m。

f.最优解的处理。同时满足个数最少且保证系统全局可观测的PMU配置不止一种，从中选取系统量测冗余度最大的一组解作为最终解，至此完成第1阶段的PMU配置S1，得到PMU个数n1。

g.求第2阶段的PMU配置S2。将步骤f中解S1作为初始解，运用改进遗传禁忌搜索算法进行求解，同时保证求解过程不改变S2中PMU的安装位置，从中选取所有节点量测冗余度之和最大的一组解作为S2。

3.3 算法流程

通过对编码方式的确定、目标模型的建立、多阶段配置的分析，以及改进遗传禁忌搜索算法的设计，可以得到多阶段PMU优化配置的算法流程，见图2。

4 算例分析

4.1 新英格兰39节点系统

为了验证改进遗传禁忌搜索算法的有效性，在Visual C++平台上编制了2阶段PMU优化配置的程序，得到基于多阶段配置模型的PMU配置结果。参数设置如下:群体数为100，最大迭代次数为100，GA交叉概率设置为0.8，变异概率设置为0.2，TS算法中禁忌表长度为。

设系统扩展规划也分成2个阶段。母线25，37，线路 2－25，3－4，21－22，25－26，25－37，母线 37 处发电机以及母线25处负荷为第2阶段新增部分。节点1，9的冗余度为2且零功率注入，节点30～38的量测冗余度为1。因此，在第2阶段配置结束后需要保证这些节点可观测，即R＞0。

首先进行第1阶段满足全网可观测的配置。应用改进遗传禁忌搜索算法，得到配置 S1为{3，8，13，16，20，23，29}，此时=S1，所需 PMU 数目 n1=7，系统量测冗余度为42。在此基础上进行第2阶段PMU的配置，得 S2为{2，3，6，8，13，16，20，22，23，25，26，29，37}。因此为{2，6，22，25，26，37}，n2为 6。系统量测冗余度为58。

运用改进前和改进后的遗传禁忌搜索算法对新英格兰39节点系统进行2阶段PMU配置，结果表明，第1阶段和第2阶段用未改进的算法求得的PMU数分别为8和7，改进遗传禁忌搜索算法求得的PMU配置个数分别为7和6。显然，改进的遗传禁忌搜索算法能够搜到比较好的解。

图2 多阶段PMU配置算法流程Fig.2 Flow chart of multistage PMU placement

分别运用最小生成树算法［5］和非支配排序遗传算法［4］，以及改进遗传禁忌搜索算法对系统进行N－1故障情况下PMU的优化配置，算法比较如表1所示。

可以看出，最小生成树法求得的PMU数目远多于其余2种算法，配置效果不佳。非支配排序遗传算法由于采用多目标进化算法，在解的个数上占有优势。采用改进遗传禁忌搜索算法求出的PMU配置数目与非支配排序遗传算法相同，但这一结果是在满足包含第1阶段解的约束下得到的。同样的PMU数目，改进遗传禁忌搜索算法能够获得更大的系统量测冗余度。

4.2 IEEE 118节点系统

设定母线10，91，以及与之相关的发电机、线路、负荷为系统扩展规划后第2阶段新增部分。采用改进遗传禁忌搜索算法，对IEEE 118节点系统进行多阶段PMU优化配置，得n1，n2分别为29，25。配置结果如表2所示。

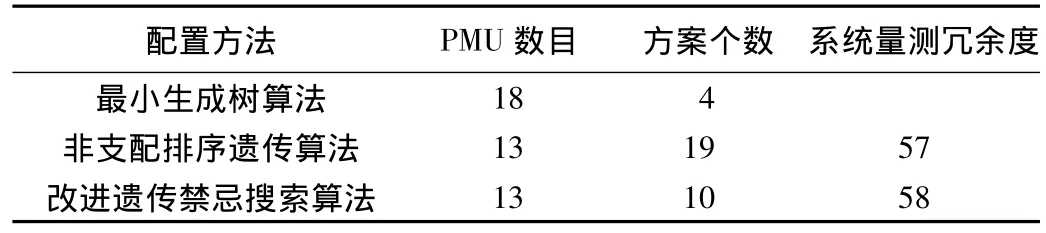
表1 新英格兰39节点系统N-1故障情况下PMU配置方案算法比较Table 1 PMU placement algorithm comparison for New England 39-bus under N-1 fault

表2 IEEE 118节点系统两阶段PMU配置结果Table 2 Results of two-stage PMU placement for IEEE 118-bus

应用改进遗传禁忌搜索算法，IEEE 118节点系统经过第1阶段配置后，满足系统可观测所需的PMU个数为29。经第2阶段后，解得满足N－1故障情况下系统可观测的PMU个数为54，而文献［3］中结果为52。这主要是因为本文第2阶段的解是在含约束条件下求得的，即包含第1阶段的解。但2个结果相差不大，且比起最小生成树法PMU数72有明显优势，表明多阶段PMU优化配置方法能把握整体的配置方向，且保证每一阶段安装的PMU都能发挥最大效用，并很好地协调了PMU配置的经济性和可靠性。

5 结 语

为解决电力系统PMU配置问题，提出一种考虑量测冗余度的多阶段PMU优化配置方法:(a)给出系统量测冗余度的计算方法;(b)建立多阶段PMU优化配置模型;(c)采用改进遗传禁忌搜索算法进行求解。该方法同时考虑系统量测冗余度和多阶段配置问题，很好地兼顾了PMU监测的经济性和可靠性，为PMU的优化配置提供了有力的决策支持。

［1］闵勇，丁仁杰，韩英铎，等.一次系统事故的同步相量测量结果分析［J］.电力系统自动化，1998，22(7):10-13.(MIN Yong，Ding Renjie，HAN Yingduo，et al.Analysis of synchronized phasor measurement result of a fault in Heilongjiang eastern power system［J］.Automation of Electric Power Systems，1998，22(7):10-13.(in Chinese))

［2］王茂海，齐霞，牛四清，等.基于相量测量单元实测数据的变压器参数在线估计方法［J］.电力系统自动化，2011，35(13):61-64.(WANG Maohai，QI Xia，NIU Siqing，et al.Online estimation of transformer parameters based on PMU measurements［J］.Automation of Electric Power Systems，2011，35(13):61-64.(in Chinese))

［3］王勇，鞠平.部分节点引入相量测量的状态估计［J］.河海大学学报:自然科学版，2004，32(3):316-319.(WANG Yong，JU Ping.Study on state estimation with PMU equipped at partial nodes of power system［J］.Journal of Hohai University:Natural Sciences，2004，32(3):316-319.(in Chinese))

［4］MILOSEVIC B，BEGOVIC M.Nondominated sorting genetic algorithm for optimal phasor measurement placement［J］.IEEE Trans on Power System，2003，18(1):69-75.

［5］DENEGRI G B，INVERNIZZI M，MILANO F，et al.A security oriented approach to PMU positioning for advanced monitoring of a transmission grid［C］//中国电力科学研究院.2002 International Conference on Power System Technology，Kunming，昆明:云南科技出版社，2002.

［6］NUQUIR F，PHADKE A G.Phasor measurement unit placement techniques for complete and incomplete observability［J］.IEEE Trans on Power Delivery，2005，20(4):2381-2388.

［7］陈晓刚，陶佳，江全元，等.考虑高风险连锁故障的 PMU配置方法［J］.电力系统自动化，2008，32(4):11-14.(CHEN Xiaogang，TAO Jia，JIANG Quanyuan，et al.an algorithm for PMU configuration considering high risk cascading failure［J］.Automation of Electric Systems，2008，32(4):11-14.(in Chinese))

［8］DUA D，DAMBHARE S，GAJBHIYE R K.Optimal multistage scheduling of PMU placement:an ILP approach［J］.IEEE Trans on Power Delivery，2008，23(4):1812-1820.

［9］AMINIFAR F，FOTUHI-FIRUZABAD M，SHAHIDEHPOUR M，et al.Probabilistic multistage PMU placement in electric power systems［J］.IEEE Trans on Power Delivery，2011，26(2):841-849.

［10］MARIN F J，GARCIA-LAGOS F，JOYA G，et al.Genetic algorithms for optimal placement of phasor measurement units in electrical networks［J］.IEEE Electronics Letters，2003，39(19):1403-1405.

［11］邢文训，谢金星.现代优化计算方法［M］.2版.北京:清华大学出版社，2005.

［12］彭疆南，孙元章，王海风.考虑系统完全可观测性的PMU最优配置方法［J］.电力系统自动化，2003，27(4):10-16.(PENG Jiangnan，SUN Yuanzhang，WANG Haifeng.An optimal PMU placement algorithm for full network observability［J］.Automation of Electric Systems，2003，27(4):10-16.(in Chinese))

［13］罗日成，李卫国.配电网电气连通性分析的快速算法研究［J］.电网技术，2004，28(24):52-55.(LUO Richeng，Li Weiguo.Research on high-speed algorithm for electrical connectivity analysis of distribution networks［J］.Power System Technology，2004，28(24):52-55.(in Chinese))