一种基于最小二乘支持向量机的葡萄酒品质评判模型

吴瑞红，王亚丽，张环冲，王鲜芳

（河南师范大学 计算机与信息技术学院，河南 新乡453003）

葡萄酒具有特殊的营养价值和医疗保健作用，是食品工业的重要组成部分 .如何对葡萄酒科学分类，提高葡萄酒的质量，对促进行业健康发展具有重要的实际意义.人们一直靠感官来判定葡萄酒质量的好坏，而感官鉴定受到多种因素的影响，其准确性难以得到保证.国内外对葡萄酒质量评判的研究主要有遗传神经网络［1］、模糊神经网络［2］、数据挖掘［3］和贝叶斯［4］等算法.本文针对通过感官鉴别葡萄酒质量的准确性难以保证的问题，建立一种基于最小二乘支持向量机学习算法的酒质量评判模型.

1 最小二乘支持向量多元分类器

1.1 最小二乘支持向量机原理

Suykens等［5］提出的最小二乘支持向量机（LS-SVM）是标准支持向量机［6-8］的一种改进.它将标准支持向量机中的不等式约束改为等式约束，且将误差平方和损失函数作为训练集的经验损失 .这样就把解二次规划问题转化为求解线性方程组问题，提高求解问题的速度和收敛精度.

设定训练集｛xi，yi则最小二乘支持向量机优化问题表示为

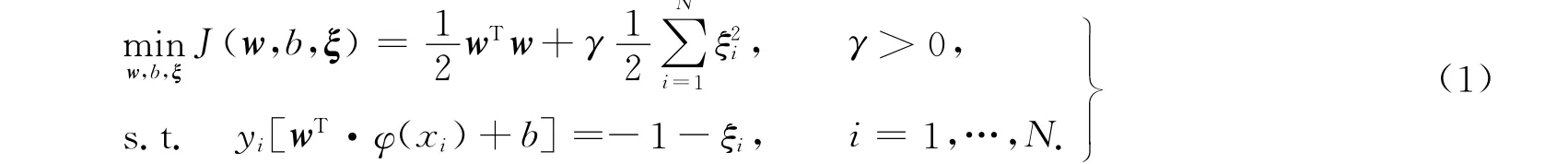
式（1）中：ξi≥0是允许错分的松弛变量；γ为错误惩罚分量.

通过式（1）的对偶形式可以求它的最优解，而对偶形式可以根据目标函数和约束条件建立拉格朗日函数 .即

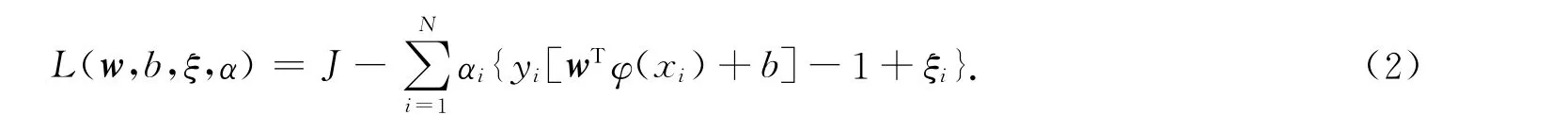
式（2）中：αi是Lagrange乘子.

按照 KKT（Karush-Kuhn-Tucker）条件［9］对式（2）进行优化，分别对w，b，ξi，αi求导，即有

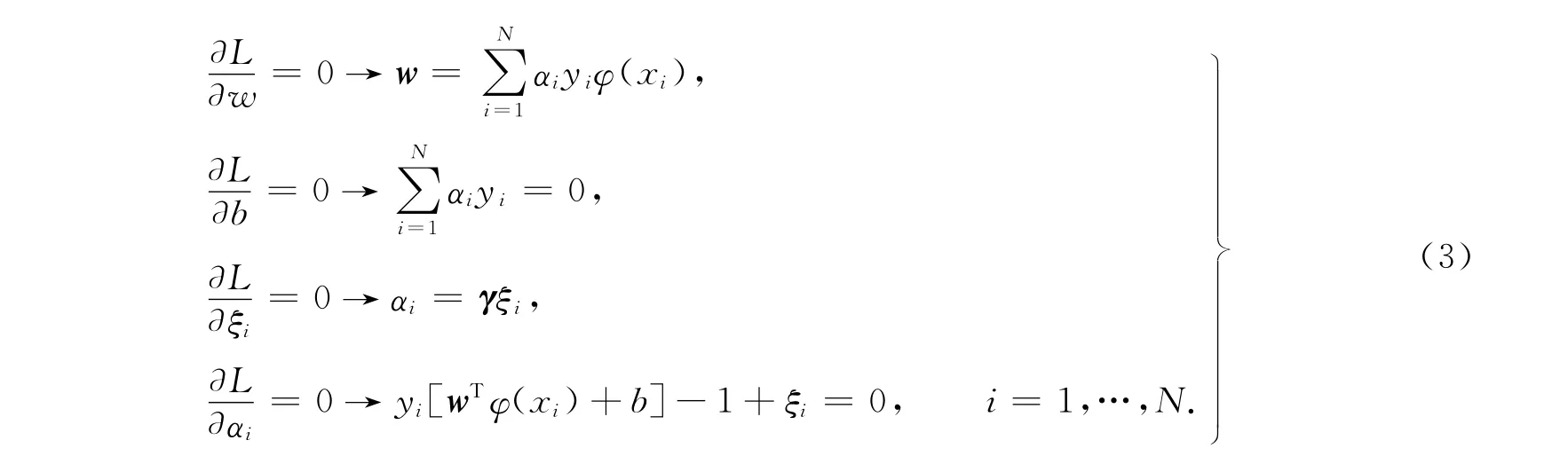
式（3）能被直接表示为

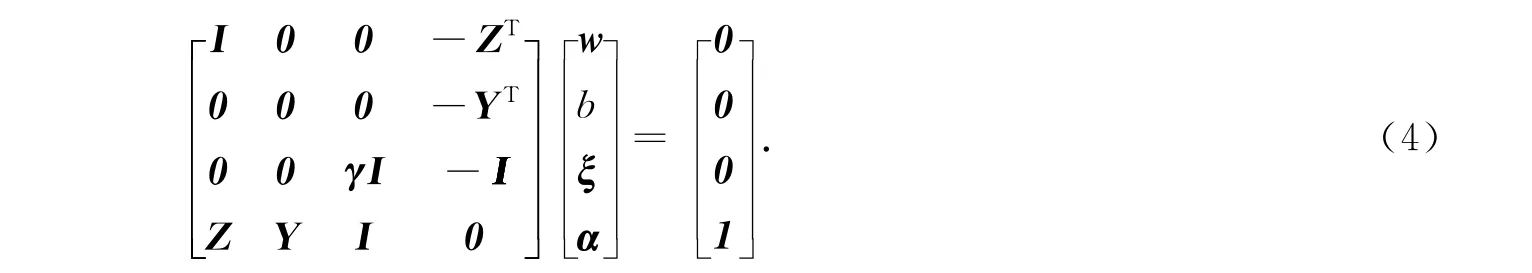
式（4）中：Y＝［y1，…，yN］，ξ＝［ξ1，…，ξN］，α＝［α1，…，αN］，Z＝［φ（x1）Ty1，…，φ（xN）TyN］，1＝［1，…，1］，I是单位矩阵.w和ξ的值可以从式（3）得出，那么式（4）可以表示为

根据文献［9］中的Mercer定理，可以实用核函数K（·，·），即

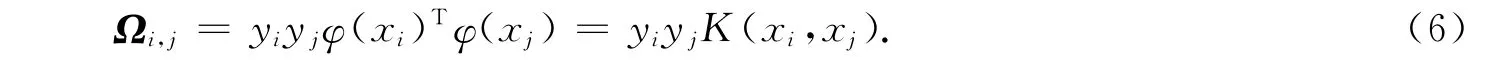
常用的核函数有多项式核、高斯核、感知器核和B样条核［10］.文中建模选用的是高斯核函数，即径向基核函数，其形式为

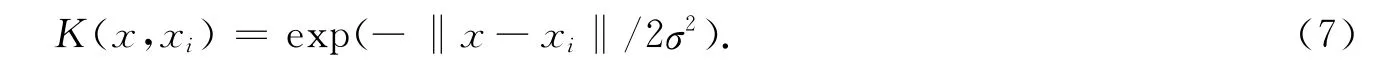
式（7）中：σ为核宽度参数.

通过式（5），（6）就可以得到分类器，避免了标准的SVM中相对复杂的二次规划问题.所求出的α，b可以得到训练集的分类决策函数，其表达式为

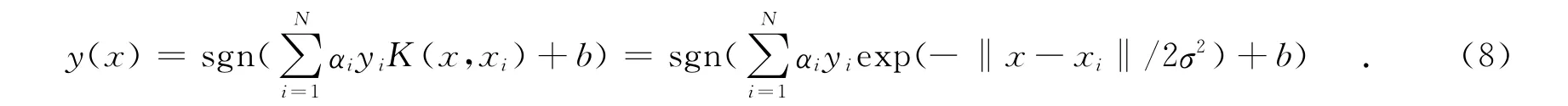
1.2 多元分类最小二乘支持向量机的构建

多分类支持向量机常用的方法有4种：一对多、一对一、导向无环图、二叉树.“一对一”的分类方法虽计算复杂，但精度高，适合类别数目较少的情形［11］.因此，基于文献［11，12-16］的思想，设计了基于最小二乘支持向量机（LS-SVM）的多元分类器.文中采用“一对一”（OAO）的方法进行多元分类，该方法是基于两类问题的分类方法，但两类问题是从原来的多类问题中抽取的.应用该方法需要构建k（k-1）／2个二元分类器，也就是需要构建k（k-1）／2个决策函数，k为所需分类问题的种类数.

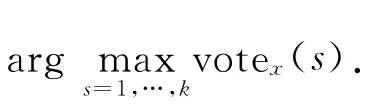
2 仿真实验分析

2.1 葡萄酒品质评判模型

为了验证构建的多元分类器的预测准确率，对 UCI机器学习数据库（http：／／archive.ics.uci.edu／ml／datasets／Wine）中的葡萄酒数据集进行仿真实验.该数据集共包括178个样本，分成3类，第1类的样本有59个，第2类的样本有71个，第3类的样本有48个.每个样本含有13个特征分量，分别是Al-cohol，Malic acid，Ash，AlKalinity of ash，Magnesium，Total phenols，Flavanoids，Nonflavanoid phenols，Proanthocyanins，Color intensity，Hue，OD280／OD315of diluted wines，Proline，这些特征分量作为分类器的输入数据X.图1为葡萄酒数据可视化图.

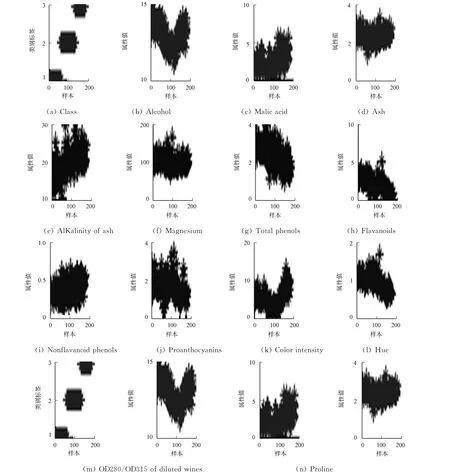
图1 葡萄酒数据的分维可视化图Fig.1 Fractal dimension visual figure of wine data

所研究的葡萄酒品质有3类，基本的LS-SVM是基于两类的，必须应用多元分类LS-SVM，即采用OAO LS-SVM方法对葡萄酒进行分类.在OAO LS-SVM分类方案中，要想对葡萄酒进行分类，需要构建3个二元分类器 .二元分类决策函数表达式为式（10），再结合式（9），可以构建出基于LS-SVM的葡萄酒品质多元分类器.

为了提高分类准确率，对数据集进行归一化预处理，采用的归一化映射为

式（11）中：x，y∈Rn；xmin＝min（x）；xmax＝max（x）归一化的效果是原始数据被规整到［0，1］范围内，即yi＝［0，1］，i＝1，2，…，n.

2.2 分类结果

仿真运用的平台为Windows 7，4G内存，软件为MATLAB（R2010b）.为了验证模型的健壮性和适应性，对预处理过的178个葡萄酒样本采取随机采样的方法选取训练集，每次从全体数据中随机的选择1／2作为训练集，其余的数据作为测试集，即实验时训练集样本为89，测试集样本为89.

利用式（9），（10）构建的多元分类器，以及文献［7］中的交叉验证方法得到相关参数.LS-SVM对训练集训练时，多维无约束非线性优化问题采用Nelder-Mead单纯形算法［18］，即为Simplex.最好分类结果如图2所示.LS-SVM对4次随机采样的训练结果，如表1所示.表1中：N为运行次数；γ为惩罚系数；σ为核参数；t为运行时间；φ为准确度.

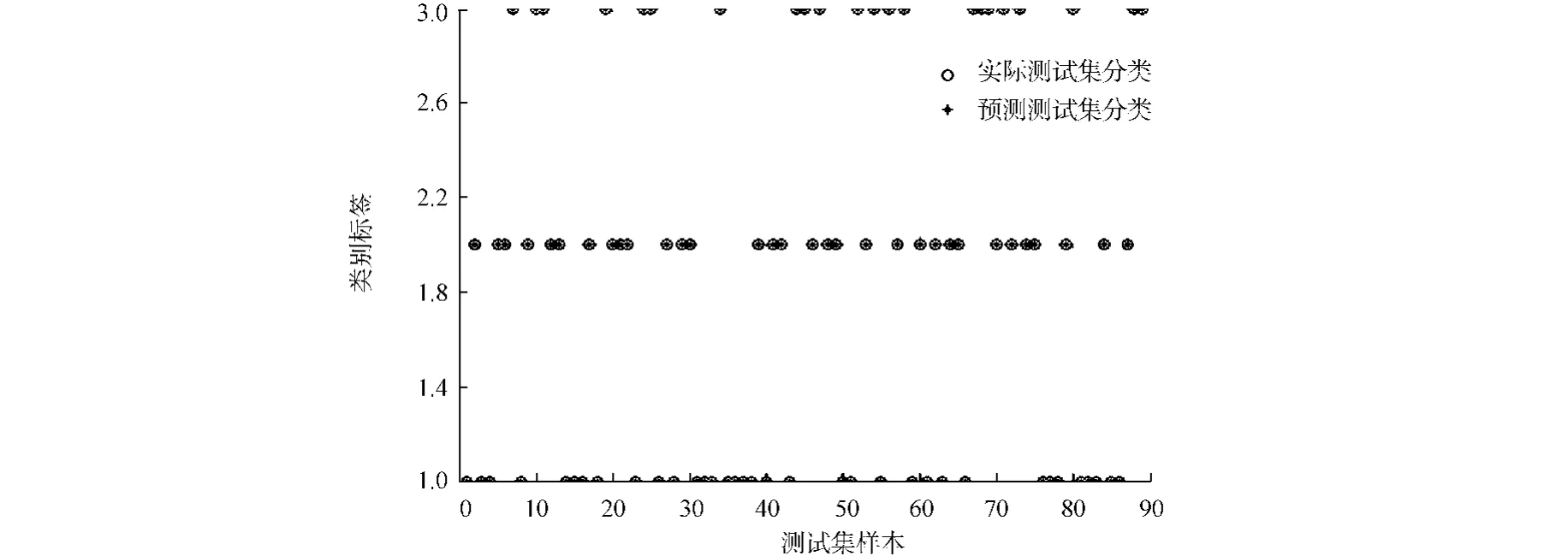
图2 LS-SVM多元分类器分类结果可视化图Fig.2 Visual figure of classified results with LS-SVM multi-classifier

为了证明所构筑分类器的分类性能，在同样的输入数据和测试数据的条件下，分别又构筑了SVM和BP神经网络多元分类器［17］.SVM同样采用［17］中的交叉验证得到相关参数，取值和分类结果如表2所示.

表1 LS-SVM多元分类器的分类结果Tab.1 Classified results with LS-SVM multi-classifier

表2 SVM多元分类器的分类结果Tab.2 Classified results with SVM multi-classifier

在BP神经网络多元分类器中，输入层取13个节点，隐含层取8个节点，输出层取3个节点.其最佳隐含层节点数选择参考如下公式，即

式（12）中：n为输入层节点数；l为隐含层节点数；m为输入出层节点数；a为0～10之间的常数.学习速率为0.1，惯性系数为0.01.表3为BP分类器的分类结果.BP，SVM，LS-SVM分类方法的比较结果，如表4所示 .表4中的平均运行时间（tav）、平均分类准确率（φav）分别从表1～3中计算得出.

表3 BP多元分类器分类结果Tab.3 Classified results with BP multi-classifier

从表4可见：最小二乘支持向量机其健壮性和适应性最好，其平均分类准确率最高为98.315%，且收敛速度最快.标准支持向量机的分类准确率次之为98.3146%，收敛速度较慢.这是因为最小二乘支持向量机把解二次规划问题转化为求解线性方程组问题，提高求解问题的速度和收敛精度，且所需计算资源少.LS-SVM最高分类准确率达到100%，表明当训练参数和训练样本选择最佳情况时，LS-SVM分类准确率也将达到最佳.与BP神经网络分类方法所得结果比较发现：SVM和LS-SVM分类器均具有较高的准确率.这说明支持向量机能较好地解决小样本、非线性等实际问题，具有很强的泛化能力.

表4 不同分类方法的结果对比Tab.4 Comparison of different classified methods′results

模型的参数最终取使得训练集验证分类准确率最高的那组γ和σ做为最佳参数，如有多组γ和σ对应于最高的验证分类准确率，则取能够达到最高分类准确率中参数γ最小的那组γ和σ做为最佳的参数，如果对应最小的γ有多组σ，就选取搜索到的第1组γ和σ做为最佳参数.

3 结论

针对通过感官鉴别葡萄酒质量的准确性难以保证的问题，建立了一种基于最小二乘支持向量机学习算法的葡萄酒质量评判模型.同时，用BP神经网络、标准支持向量机分类器对葡萄酒进行训练.

从BP神经网络、标准支持向量机和最小二乘支持向量机3种分类准确率及运行时间对比，最小二乘支持向量机平均分类准确率最高，所能达到的最高分类准确率为100%.由此可见，最小二乘支持向量机在模式分类问题上能提供好的泛化性能，求解速度快，求解所需的计算资源较少.

运用交叉验证方法选取惩罚系数和核参数来训练分类器是有效的.“一对一”算法为多元分类器实现提供了很好的方法，虽其计算复杂，但精度高，适合类别数目较少的情形.最小二乘支持向量机能较好地解决小样本、非线性等实际问题，在葡萄酒品质评判中具有很大应用潜力.

［1］ 殷勇，邱明，刘云宏，等.基于遗传神经网络的酒类鉴别技术［J］.农业机械学报，2003，34（6）：104-106.

［2］ RAPTIS C G，SIETTOS C I，KIRANOUDIS C T，et al.Classification of aged wine distillates using fuzzy and neural network systems［J］.Journal of Food Engineering，2000，46（4）：267-275.

［3］ CORTEZ P，CERDEIRA A，ALMEIDA F，et al.Modeling wine preferences by data mining from physicochemical properties［J］.Decision Support Systems，2009，47（4）：547-557.

［4］ BELTRÁN N H，DUARTE-MERMOUD M A，et al.Feature extraction and classiication of Chilean wines［J］.Journal of Food Engineering，2006，75（1）：1-10.

［5］ SUYKENS J K，VANDEWALLE J.Least squares support vector machine classifiers［J］.Neural Processing Letter，1999，9（3）：293-300.

［6］ VAPNIK V N.The nature of statistical learning theory［M］.New York：Pringer-Verlag，1995.

［7］ VAPNIK V N.Statistical learning theory［M］.New York：Pringer-Verlag，1998.

［8］ HE Xi-sheng，ZHE Wang，Cheng Jin，et al.A simplified multi-class support vector machine with reduced dual optimization［J］.Pattern Recognition Letters，2012，33（1）：71-82.

［9］ CRISTIANINI N，SHAWE-TAYLOR J.An introduction to support vector machines and other kernel-based learning methods［M］.Cambridge：The Press Syndicate of Cambridge University，2000.

［10］ 潘立登，李大字，马俊英.软测量技术原理与应用［M］.北京：中国电力出版社，2009.

［11］ WANG Tai-yue，CHIANG Huei-min.One-against-one fuzzy support vector machine classifier：An approach to text categorization［J］.Expert Systems with Applications，2009，36（6）：10030-10034.

［12］ 朱家元，郭基联，张恒喜，等.多元分类LS-SVM设计与装备保障性评估［J］.装备指挥技术学院学报，2003，14（3）：12-15.

［13］ VEENMAN C J，BOLCK A.A sparse nearest mean classifier for high dimensional multi-class problems［J］.Pattern Recognition Letters，2011，32（6）：854-859.

［14］ 陈志刚，连香姣，于会媛，等.多元支持向量机在压缩机故障诊断中的应用［J］.石油机械，2009，37（11）：63-65.

［15］ LI Xiao-li，NIE Peng-cheng，QIU Zheng-jun，et al.Using wavelet transform and multi-class least square support vector machine in multi-spectral imaging classification of Chinese famous tea［J］.Expert Systems with Applications，2011，38（9）：11149-11159.

［16］ FU Jui-hsi，LEE Sing-ling.A muti-class SVM classification system based on learning methods from indistinguishable chinese official documents［J］.Expert Systems with Applications，2012，39（7）：3127-3134.

［17］ 史峰，王小川，郁磊，等.MATLAB神经网络30个案例分析［M］.北京：北京航空航天大学出版社，2010.

［18］ CHELOUAH R，SIARRY P.A hybrid method combining continuous tabu search and Nelder-Mead simplex algorithms for the global optimization of multiminima functions［J］.European Journal of Operational Research，2005，161（3）：636-654.