涡旋光束嵌套高斯光束在湍流大气中的传输

赵艮春，庄其仁，陈唐荣，戴文海

（华侨大学 信息科学与工程学院，福建 厦门361021）

带有涡旋相位因子的涡旋光束具有许多独特的性质，如深聚焦特性、轨道角动量特性、中心光学奇点等，因而在囚禁和操控原子及其他微粒中得到广泛的应用.与此同时，涡旋光束还具有额外的自由度，有望用于空间光通信.由于光束轨道角动量数只受诸如光学孔径等实际条件的限制，因此，相对于传统的二进制编码，采用光轨道角动量编码能够有效地提高数据传送密度和据传速率 .同时，由于光轨道角动量编码需要全光束接收，部分拦截不能获得全部光信息，因此具有通信保密特性［1-2］.当涡旋光束在大气中传输时，由于受到大气湍流的影响，引发接收面上光束畸变，最终导致光束质量下降，对实际应用形成严重的限制［3-11］.如何降低大气湍流对涡旋光束空间光通信质量的影响，是亟待解决的问题［7-8］.为此，提出一种涡旋光束嵌套高斯光束的光束大气传输方案，使涡旋信号光束和高斯参考光束同时通过相同的大气湍流环境，在接收端对两光束进行相干检测，以期消除大气湍流引起的强度起伏的影响.本文介绍一种涡旋光束嵌套高斯光束的复合光束产生方法及其在湍流大气中的传输特性.

1 涡旋光束嵌套高斯光束的理论模型

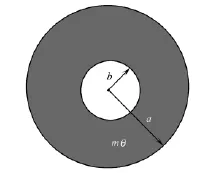
图1 螺旋相位板示意图Fig.1 Schematic of spiral phase plate

图1为一中空相位板.该相位板的作用是可以使位于半径b＜ρ＜a区域的入射光束产生一个随方位角变化的相位延迟，即涡旋光束，而位于半径ρ＜b区域的入射光束保持原状态传输.因此，入射高斯型激光束经中空相位板后，将形成涡旋光束嵌套高斯光束的复合光束.

当入射光束为He-Ne激光的准直扩束光束时，透过半径r＜b的场强依然是高斯型的，而透过半径b＜r＜a的场强是涡旋高斯型的 .傍轴近似下，在柱坐标系ρ，θ，z中，以E0表示空间均匀场振幅，ρ表示光束发射平面内任意一点的归一化径向坐标，即光束发射平面内任意一点到中心的径向距离与发射口半径的比值，θ为z＝0平面内的方位角坐标，γ为某一个对激光束束腰宽度ω0起限定作用的参数，光束光强的峰值取决于m，ω0和E0.

位于初始平面z＝0（螺旋相位板所在的平面）的涡旋光束嵌套高斯光束的场分布可表示为

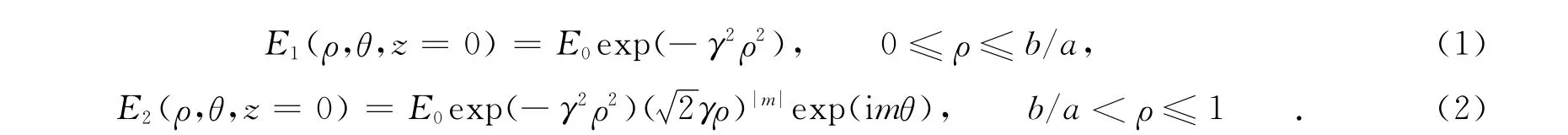
式（2）中：m为涡旋光束的拓扑电荷数.

为计算方便，设E0＝1，利用菲涅尔-基尔霍夫衍射积分方程，可得涡旋光束嵌套高斯光束经湍流大气传输后到达距离发射面为z距离的接收焦面处的光波复振幅，即

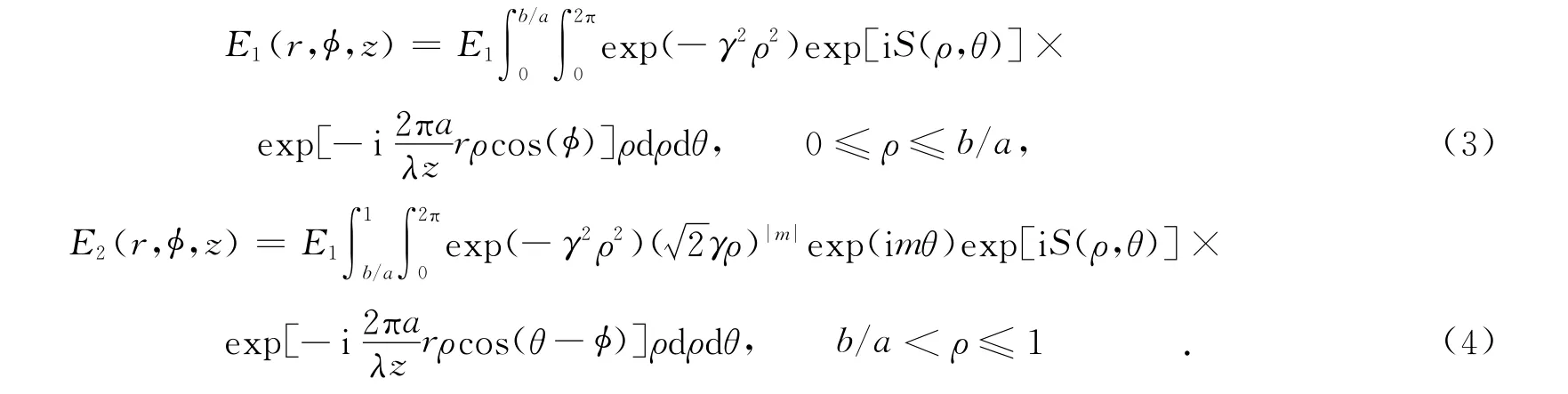
式（3），（4）中：S（ρ，θ）为波像差函数［8，12］.

在湍流散焦单独存在时，S（ρ，θ）＝a4z4（ρ，θ）＝（2ρ2-1）.其中：〉＝0.007

在湍流象散单独存在时，S（ρ，θ）＝（a5ρ2cos 2θ+a6ρ2sin 2θ）.其中：〉＝0.023（D／r0）5／3＝0.007（D／0）5／3.

以〈·〉表示湍流统计的系综平均，则焦平面上湍流统计系综的平均光强可以表示为

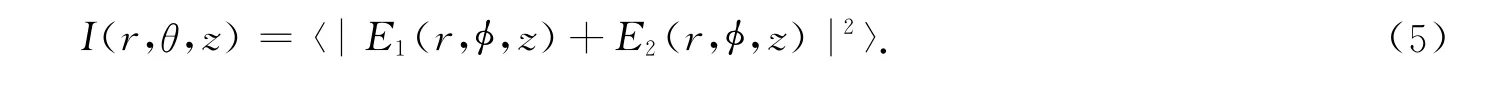
2 数值模拟和讨论

在大气折射率结构常数（C2n）分别为0m-2／3，10-15m-2／3，10-14m-2／3，5×10-14m-2／3，光束传输距离z分别为1 000，3 000，5 000m的情况下，对不同拓扑电荷数的涡旋光束嵌套高斯光束接收焦面处的光强分布情况进行数值模拟计算，结果如图2，3所示.图2，3中：横坐标x表示接收焦面内x轴上任意一点到焦面中心的径向距离；纵坐标I表示接收焦面内的光强分布.

从图2，3可知：随着大气折射率结构常数C2n的增大，接收焦面内光强的峰值逐渐减小；当大气折射率结构常数一定时，随着光束传输距离z的增加，接收焦面内光强的峰值也逐渐减小，光束逐渐扩展；随着拓扑荷数增大，光束扩展和光斑漂移现象也越明显.说明大气湍流波像差中的散焦和像散对涡旋光束嵌套高斯光束这一复合光束，在光斑强度、光斑扩展和光斑位置漂移方面影响明显.

由图2，3还可知：像散和散焦对接收焦面内光强分布的影响规律基本相同，随着湍流强度和传输距离的增大，像散较散焦对接收焦面内光强分布的影响更明显 .主要表现在光强峰值衰减更大，光束扩展、光束漂移现象更加明显.值得注意的是，无论是大气折射率结构常数、传输距离，还是拓扑电荷数的变化，涡旋光束嵌套高斯光束在接收焦面内的光强分布仍保持其高斯分布规律.说明涡旋光束和高斯光束经大气湍流后具有相同的强度起伏，有利于作为信号光和参考光的干涉和后续处理.

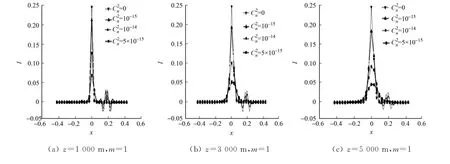
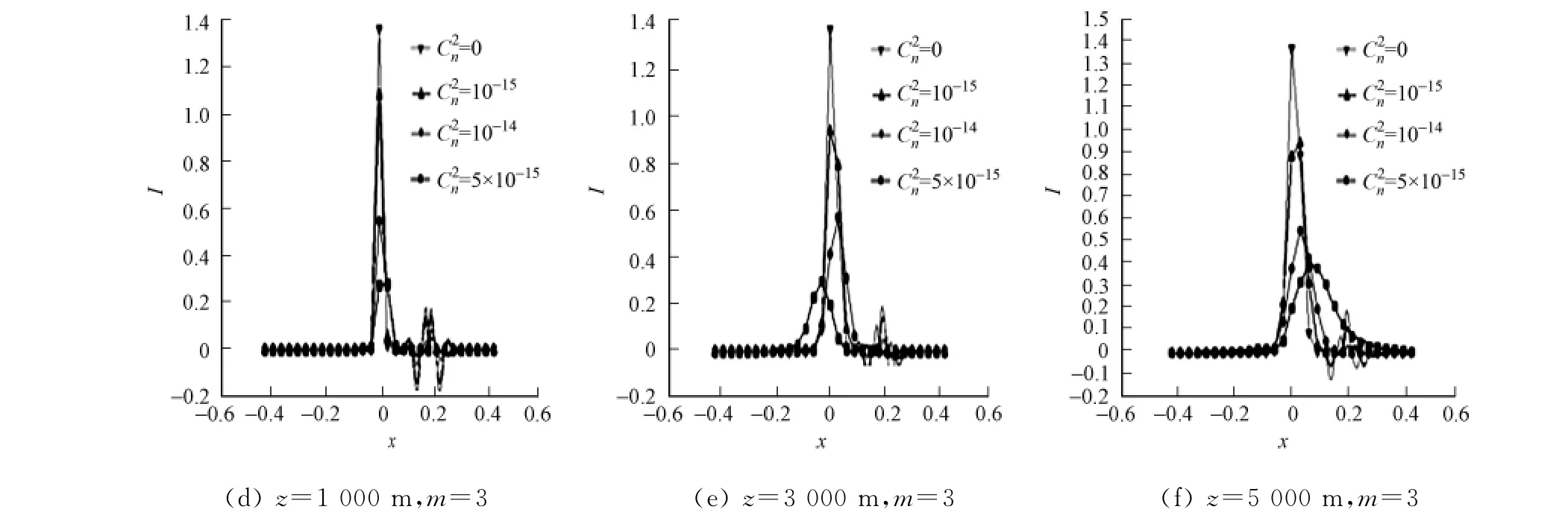
图2 散焦对涡旋光束嵌套高斯光束焦面光强的影响Fig.2 Impact of defocus to the intensity of the focal plane of the vortex beams nested Gaussian beams

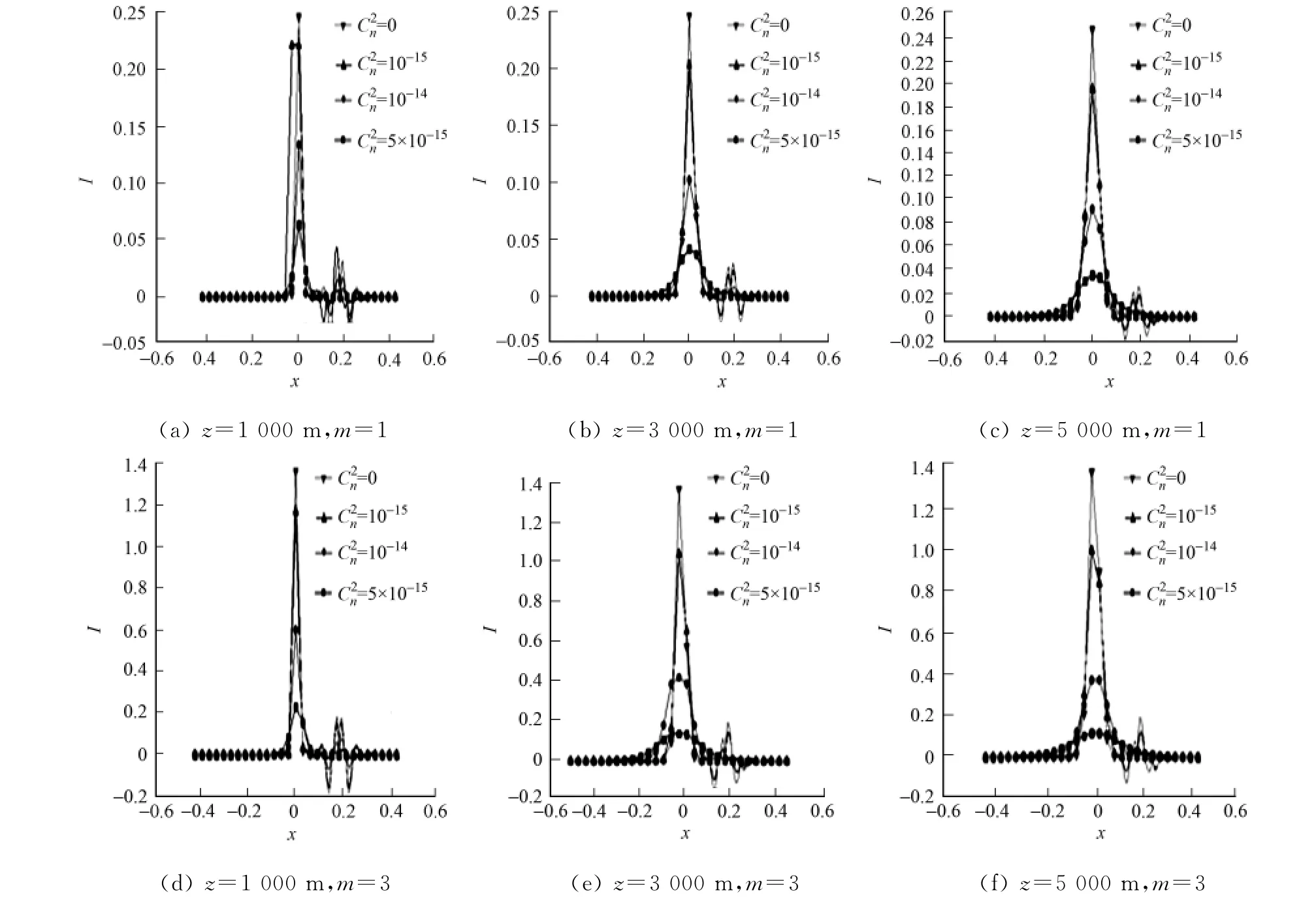
图3 像散散焦对涡旋光束嵌套高斯光束焦面光强的影响Fig.3 Impact of astigmatism defocus to the intensity of the focal plane of the vortex beams nested Gaussian beams

3 结论

采用中空相位板可产生涡旋光束嵌套高斯光束，利用波像差函数研究大气湍流像差散焦和像散对涡旋光束嵌套高斯光束接收焦面光强的影响 .结果表明：随着传输距离和大气折射率结构常数的增大，复合光束焦面光强峰值降低，光斑半径增大，光斑漂移现象明显.

但无论是大气折射率结构常数、传输距离，还是拓扑电荷数的变化，涡旋光束嵌套高斯光束在接收焦面内的光强分布仍保持其高斯分布规律 .说明涡旋光束和高斯光束经大气湍流后具有相同的强度起伏，若将涡旋光束作为信号光束，高斯光束作为参考光束，就可利用此二光束的干涉图样检测出涡旋光束的拓扑荷数，并应用于大气光通信.

［1］ ZHANG Yi-xin，TANG Min-xia，TAO Chun-kan.Partially coherent vortex beams propagation in a turbulent atmosphere［J］.Chin Opt Lett，2005，3（10）：559-561.

［2］ YANG Jian-cai，HE Sai-ling.Propagation of various dark hollow beams in a turbulent atmosphere［J］.Opt Express，2006，14（4）：1367-1380.

［3］ CANG Ji，QI Wen-hui，ZHANG Yi-xin.The intensity distributions of focused partially coherent dark hollow beams in turbulent atmosphere［J］.Laser Journal，2009，30（3）：40-42.

［4］ COWAN D C，ANDREWS L C.Effects of atmospheric turbulence on the scintillation and fade probability of flattened Gaussian beams［J］.Opt Eng，2008，47（2）：026001-1-026001-14.

［5］ WANG Hua，WANG Xiang-zhao，ZENG Ai-jun，et al.Effect of atmospheric turbulence on the spatial coherence of quasi-monochromatic Gaussian Schell-model beams propagating in the slant path［J］.Chin Phys，2008，57（1）：0634-05-0634-09.

［6］ CHEN Xiao-wen，TANG Ming-yue，JI Xiao-ling.The influence of atmospheric turbulence on the spatial correlation property of partially coherent Hermite-Gaussian beams［J］.Chin Phys，2008，57（4）：2607-07-2607-13.

［7］ SINGH R K，SENTHILKUMARAN P，SINGH K.Influence of astigmatism and defocusing on the focusing of a singular beam［J］.Opt Communications，2007，270（2）：128-138.

［8］ DAI Guang-ming，MAHAJAN V N.Zernike annular polynomials and atmospheric turbulence［J］.J Opt Soc Am，2007，24（1）：139-155.

［9］ 张逸新，迟泽英.光波在大气中的传输与成像［M］.北京：国防工业出版社，1997：8-17.

［10］ JI Xiao-ling，TANG Ming-yue，CHEN Xiao-wen，et al.Spectral properties of topped beams propagating through atmospheric turbulence［J］.Acta Optica Sinica，2008，28（1）：12-16.

［11］ ZHANG Yi-xin，WANG Gao-gang.Slant path average intensity of finite optical beam propagating in turbulent atmosphere［J］.Chin Opt Lett，2006，4（10）：559-562.

［12］ 赵贵燕，张逸新.湍流大气中涡旋光束拓扑荷对焦面光强的影响［J］.江南大学学报：自然科学版，2009，8（5）：617-621.