基于代理模型技术的返回舱外形优化

马洋 荣伟 江长虹 张青斌 霍霖

（1国防科学技术大学航天科学与工程学院，长沙 410073）

（2北京空间机电研究所，北京 100094）

1 引言

采用球冠倒锥外形的返回舱在再入过程中将经历十分严酷而复杂的气动力热环境。球冠表面受气流强烈压缩，承受着高温、高压气流，气流在球冠和倒锥联结的肩部附近发生剧烈膨胀，在后体锥面上形成高速低压的流动。精心设计返回舱外形可以有效地减少严酷力热环境对其再入过程产生的不利影响，也是保证成功完成再入任务的关键点之一。返回舱在大气层内利用空气阻力减阻，要获得尽可能大的阻力以尽快减小飞行速度可以通过外形设计达到目的，但阻力的增大会受到诸多因素的制约。首先由于阻力与升阻比存在着天然的“矛盾关系”，而升阻比又是控制再入弹道、改进落点精度最关键的因素，因而在增大阻力时必须考虑到升阻比的要求。另外在高速再入过程中产生的气动加热也会对返回舱外形设计提出特殊要求。

气动特性的精确预示是进行返回舱外形优化设计的基础，陈河梧采用试验手段研究了 Ma=5~8，攻角在–27°~2°条件下，类神舟飞船返回舱的高超声速气动特性，认为返回舱球冠主导小攻角的气动力变化，大攻角时倒锥的气动力贡献加大，升力和俯仰力矩出现比较明显的非线性增量[1]。纪楚群和吕俊明采用计算流体力学(Computational Fluid Dynam ics, CFD)数值仿真手段对钟形返回舱和火星再入返回舱进行数值模拟，对比分析了基于Euler方程和Navier-Stokes(NS)方程的CFD模拟结果，并分析了化学非平衡效应的影响，研究表明，在高超声速情况下，由于物体迎风面的压力远远大于背风面压力，背风面压力计算误差对整体气动力特性影响很小，同时气流在物面的分离情况不严重，因此用 Euler方程可足够准确地预测返回舱高超声速情况的流场及气动特性[2-3]。化学非平衡效应对返回舱气动特性影响较小，但它会对激波形状和驻点位置产生影响。返回舱外形优化设计研究方面，李治宇采用Euler方法在ISIGHT集成软件环境下对返回舱外形展开优化设计，得到了升阻比和驻点热流的优化前缘[4]。John E Theisinger对火星再入返回舱外形进行了详细的气动力热分析，通过对外形进行优化分析，对阻力、配平状态下的稳定性、表面热流、驻点热流、容积率、容积、升阻比等各种相互制约的性能进行协调[5-6]。

本文气动特性分析采用三维 NS方程，不考虑真实气体的化学非平衡效应，引入代理模型以减少计算开销，采用Fay-Riddell公式计算驻点热流，并利用成熟的改进非劣分类遗传算法(Nondom inated Sorting Genetic A lgorithm-II, NSGA-II)[7]，对参数化设计的返回舱外形进行多目标优化设计，该优化设计方法在返回舱方案设计阶段具有一定的应用价值。

2 研究方法

在气动外形优化设计中，设计结果的精度和计算效率往往相互冲突。结果的精度主要由气动特性计算精度和寻优算法精度决定，本文选择经典遗传算法寻优，寻优算法精度和效率不在本文的研究之列。气动特性计算方法主要有工程估算方法、CFD数值仿真以及两种方法相结合的混合方法等。工程估算效率最高，其精度也最差，较少直接用于优化设计。CFD方法计算精度很高，许多情况下可以替代试验研究，但在飞行器气动外形优化设计中，需要反复修改气动外形，多次进行气动特性计算，采用CFD方法的计算成本即使是对最先进的计算资源来说仍显得力不从心。混合方法由于具有工程估算高效和CFD仿真高精度的潜质，在优化设计中正受到一些研究人员的重视[8-9]，但其计算精度受CFD结果和所采取的拟合算法的限制，其应用还需要进一步的研究。

本文引入代理模型技术以减小CFD计算的开销，并采用改进的EI（Expected Improvement）函数加点策略[10]，充分发挥代理模型的高效性，并以高效的加点策略保证结果的精度，很好地解决了气动外形优化设计中精度与效率的问题，具体优化设计方法如图1所示。首先采用试验设计方法产生构建代理模型的样本点，然后采用CFD方法计算样本点的气动特性，并基于计算结果构建代理模型，再判断代理模型计算结果与CFD计算结果的误差是否满足精度要求，如果不满足则按加点策略加点重新进行CFD计算并构建代理模型，直至满足收敛要求，最后用构建好的代理模型代替CFD仿真进行外形优化设计。

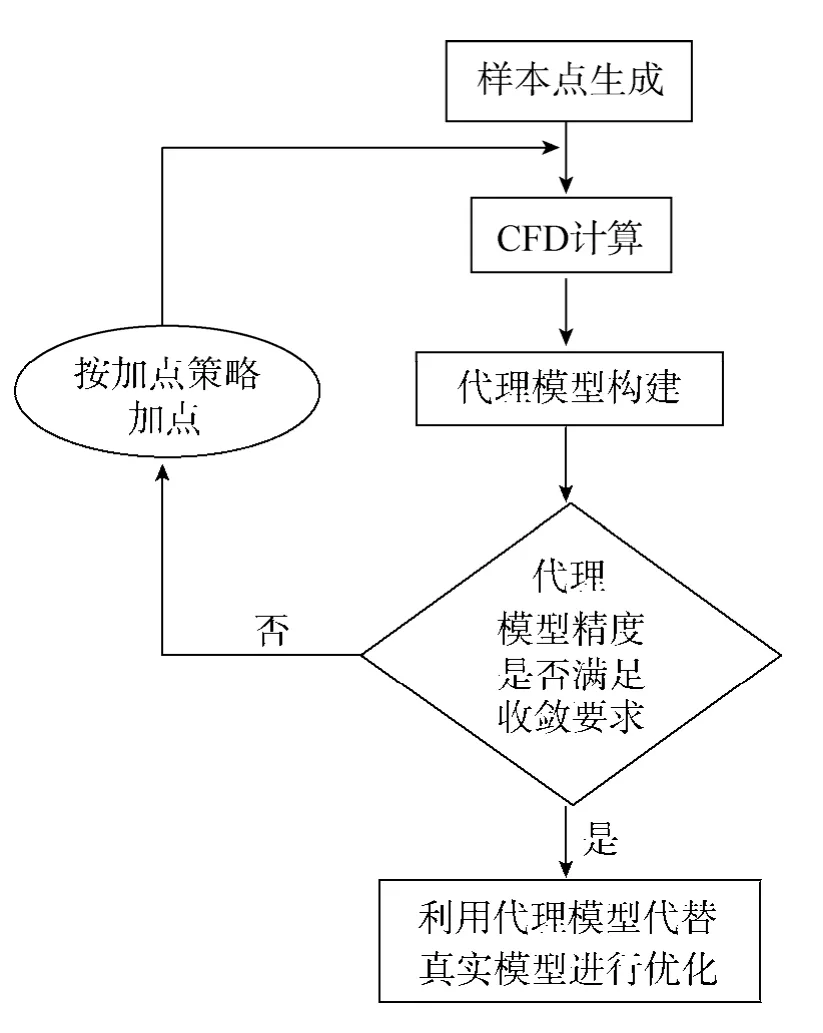
图1 优化设计流程Fig.1 Optimization design process

2.1 气动特性分析方法及验证

气动性能计算采用成熟的Fluent软件。选取可实现的k-ε两方程湍流模型，并配合使用非平衡壁面函数，这样更适合于模拟返回舱附近扰流流场中出现的大分离和大漩涡特性，对流项离散采用二阶AUSM格式，返回舱表面满足无滑移边界条件，进口取来流参数，出口数值边界条件采用外推方式获得。

采用结构网格离散流场，由于流场的对称性，只对一半流场进行网格划分，在靠近返回舱表面对网格进行加密，返回舱和用于数值精度验证的计算网格如图2和图3所示。

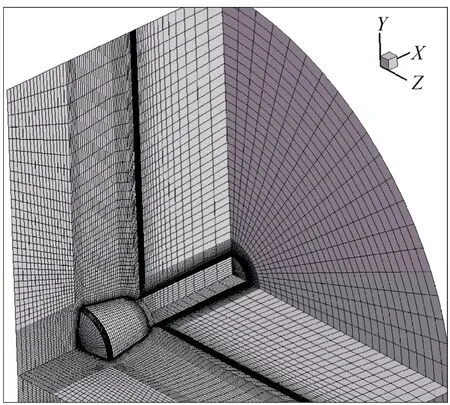
图2 返回舱计算网格Fig.2 Computing grid of reentry capsul

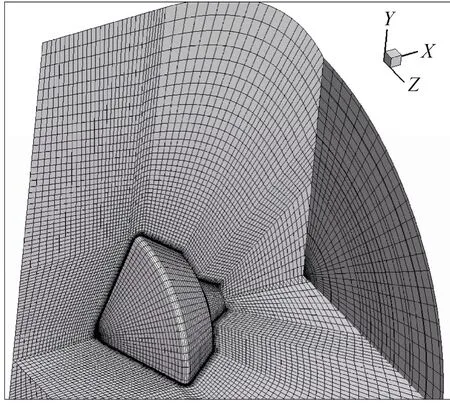
图3 数值验证算例计算网格Fig.3 Computing grid of CFD validation

为验证本文CFD计算模型的准确性，对文献[11]提供的火星探测实验飞行器外形进行数值模拟，并与文献[3]和[11]计算结果进行对比（如表1所示，其中α、CL、CD、L/D和CM分别表示攻角，升、阻力系数，升阻比和俯仰力矩系数），可以看出，本文 CFD计算得到的气动特性与文献结果的误差约为2~9%，数值仿真模型具有较高的可信度。

表1 火星探测实验飞行器气动特性计算验证Tab.1 Aerodynam ic computing accuracy verification of Mars Science Laboratory

2.2 返回舱驻点热流计算

由于热流数值仿真需要比气动力数值模拟更多的计算资源，而工程经验公式能在趋势上给出气动热与其它性能的大致协调关系，因此在方案设计阶段采用经验公式计算驻点热流不失为一种折衷的选择。返回舱驻点热流采用简化的Fay-Riddell公式[12]：

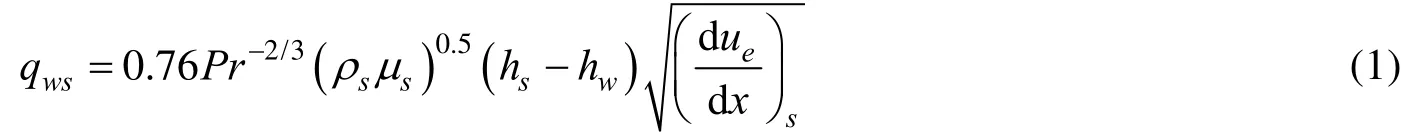
2.3 代理模型构建

代理模型技术主要包括多项式响应面(Polynom ial Response Surface)、径向基函数(Radial Basis Function)、神经网络(artificial neural networks)和Kriging方法等，前两种方法在处理非线性强和高维数问题时表现不好，神经网络方法虽然较适合处理非线性强和高维数问题，但其预测精度和鲁棒性在一定程度上不及Kriging方法[13]。

本文采用Kriging方法构建替代CFD分析的代理模型[14]，为了增强代理模型的寻优精度和效率，借鉴经典的EI函数加点方法[10]并加以改进，提出在现有样本点基础上，同时加入EI值最大的点和Kriging模型预测方差最大的点来改善模型预测精度，EI值和 Kriging模型预测方差的具体计算方法参考文献[10,14]，这样的加点寻优方法一方面具有EI函数方法兼顾局部和全局寻优的特点，另一方面在模型预测方差最大处加点更注重模型的全局精度，并且多点加点方式也适合于并行计算，有利于提高优化设计的效率。

2.4 寻优算法

遗传算法模拟生物在自然环境中的遗传和进化过程，是一种自适应、全局优化、概率搜索算法，它具有良好的鲁棒性、全局性和并行性，在当今工程技术领域的多目标优化问题中应用非常广泛。在众多的多目标遗传算法中，NSGA采用简洁明晰的非优超排序机制，使算法具有逼近Pareto最优解的能力，采用排挤机制保证得到的Pareto最优解具有良好的分布，Deb在NSGA基础上改进得到NSGA-II[15]，引入精英保留策略对产生的非劣解进行非劣快速分类和密度估计操作，比较其拥挤度，确定是否可接受为Pareto最优解。NSGA2算法提出了新的基于分级的快速非劣排序算法，大大降低了计算复杂度；同时为使Pareto最优解散布范围较大，尽可能均匀遍布，引入了拥挤距离的概念，并采用拥挤比较算子代替需要计算共享参数的适应度共享方法；最后引入精英保留机制，不但扩大了采样空间，而且有利于保持优良个体，迅速提高了种群的整体水平。由于NSGA-II算法的上述优点和可靠性，本文以其作为优化算法。

3 多目标优化与分析

3.1 返回舱外形描述

返回舱外形如图4所示，可以采用最大直径dm、最大高度H、端框直径dD和高度HD、大底半径RN、前体半径RF、大底倒圆半径 Rc和后体倾角θ来表示。

3.2 问题描述

在返回舱再入大气的过程中，需要依靠大气阻力使其减速才能完成再入返回的任务，同时返回舱也需要尽可能大的升阻比，这样能实现横向和纵向的机动，得到更宽的再入走廊，从而改善落点的精度。但是阻力和升阻比从来就存在着“矛盾”，要想得到满足再入返回要求的返回舱外形必须同时考虑这两个目标，进行多目标优化。另外在返回舱高速再入过程中，严重的气动加热是必须考虑的问题，同时为满足载人以及设备存放的要求，返回舱内的空间也是设计需要关注的地方，本文将返回舱表面最大热流（驻点热流）和容积率作为约束条件加入到优化设计过程中，以体现多种约束条件下的设计。

在图4所示的8个外形参数中，最大高度H和最大直径dm受返回舱总体规模的限制变化较小，端框直径dD和高度HD由于处在背风区对返回舱的气动力和气动热特性影响较小，对容积特性的影响也较小，它们都不适宜作为本文优化问题的设计变量。后体倾角θ虽然可变范围较大且对返回舱性能有较大影响，但在大底半径RN、前体半径RF和大底倒圆半径Rc确定的前提下，θ是确定的，即θ、RN、RF和Rc只有是3个参数是独立的。本文选取RN、RF和Rc作为设计变量，它们的取值范围如表2。

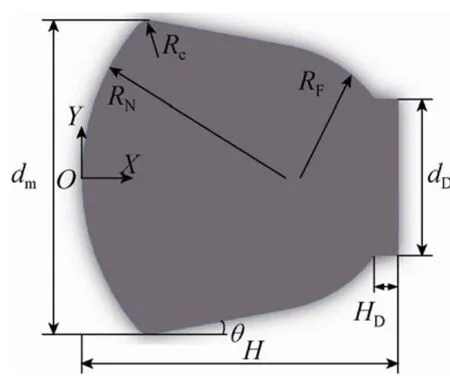
图4 返回舱外形参数Fig.4 Configuration parameters of reentry capsule

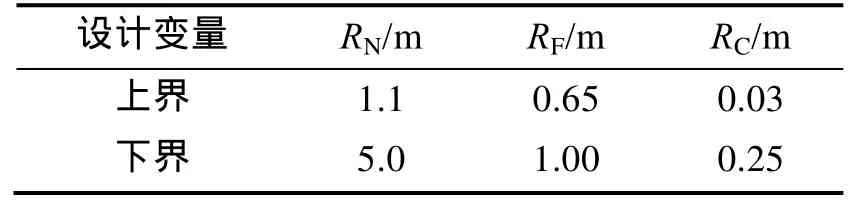
表2 设计变量及其变化范围Tab.2 Design variables and their variation range

在某一典型的再入条件下[1]，返回舱外形优化设计问题可以这样描述：

3.3 优化结果

多目标优化结果如图5所示。图中空心圆圈为优化得到的满足约束条件的前缘点，它们分布均匀，满足约束条件，并体现了两个优化目标间的冲突和妥协，设计者可以根据返回舱再入飞行的实际需求在前缘点上选择相应的气动外形；实心圆点为同时满足 CD和 L/D最大的理想状态（图中标注“Ideal”），由于优化目标相互冲突，该理想状态是达不到的；“＋”标记点表示用于构建代理模型的样本点；前缘上首尾标注“Max CD”和“Max L/D”的点为满足约束前提下，分别以CD和L/D为目标的单目标优化结果；图中标注“TPF”的点对应于某一典型的优化前缘(Typical Pareto Front，TPF)。图5还给出了样本点和前缘点上典型状态对应的返回舱外形。

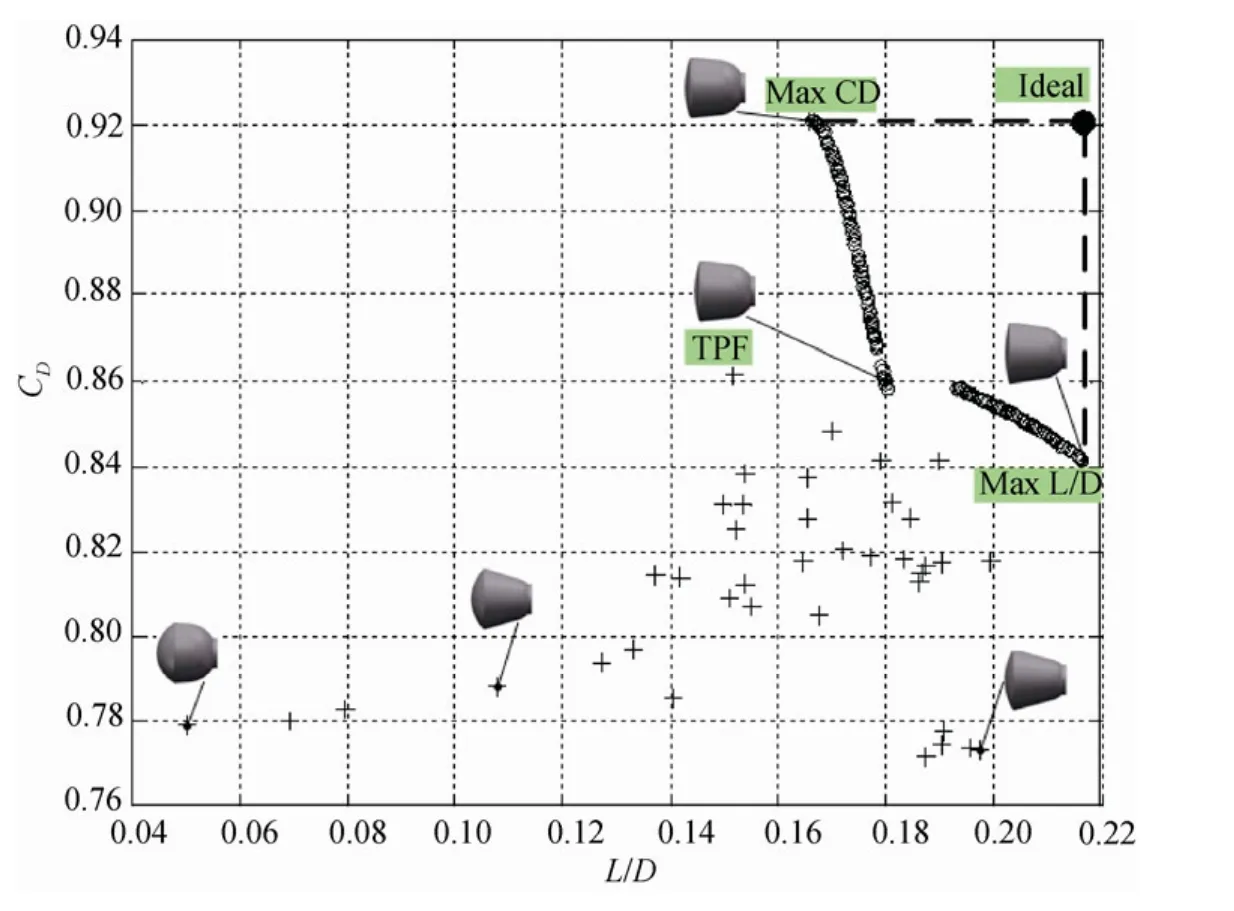
图5 多目标优化结果Fig.5 Multi-objective optim ization results

3.4 优化设计精度与效率分析

在构建代理模型时初始样本点为30个，经过3次加点迭代和模型修正后，Kriging模型最大预测方差满足收敛要求，然后随机产生4个测试点对建立的代理模型进行验证，升阻比、阻力系数和容积率的最大误差分别为6.52%、3.58%和1.24%。另外在优化前缘上选取3个标注代号为“Max CD”、“Max L/D”和“TPF”的外形，采用CFD方法计算对应的气动特性，与采用代理模型预测的结果比较，表3为阻力系数和升阻比的比较结果，可见，CFD结果与代理模型响应差别最大不超过7%。由此可见基于本文介绍的方法构建的代理模型具有较好的精度，可以替代真实物理模型进行优化设计。

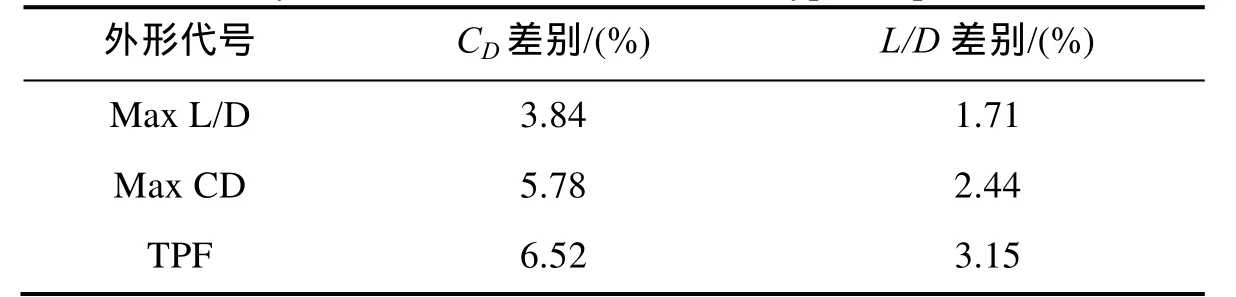
表3 典型前缘点特性验证Tab.3 Aerodynam ic character verification of typical optim ization front

本文在优化过程中，总共调用代理模型20 051次，这意味着如果气动分析直接采用CFD方法的话，总共需要进行20 051次CFD数值计算，而采用代理模型替代数值仿真后，代理模型的计算时间与CFD计算时间相比几乎可以忽略不计，整个优化过程的计算时间主要体现在构建代理模型时的40次CFD计算时间上，可见引入代理模型后，大约可以减少20 000次CFD分析时间，这样高效的分析方法十分适合返回舱总体优化设计。

4 结束语

通过对返回舱进行气动外形优化设计，得到了如下结论：

1）引入代理模型能极大提高气动特性的计算效率，同时采用改进的EI加点策略能将样本点的数目大大减少而不降低代理模型的精度，优化计算结果表明，代理模型计算结果与CFD计算结果误差可以控制在7%以内，基于代理模型技术的优化过程可以节省绝大部分（95%以上）的计算开销；

2）以返回舱升阻比和阻力系数为目标，以驻点热流和容积率为约束条件进行多目标多约束优化，得到了优化前缘，为返回舱总体设计提供了有益的借鉴。

References)

[1]陈河梧. 飞船返回舱高超声速气动特性的风洞实验分析 [J]. 航天器工程, 2008, 17(5): 77-81.CHEN Hewu. Wind-tunnel Test Analysis on Hypersonic Aerodynam ic Characteristics of Returnable Module [J]. Spacecraft Engineering, 2008, 17(5): 77-81. (in Chinese)

[2]纪楚群, 周伟江. 钟形返回舱空气动力特性数值模拟 [J]. 航天返回与遥感, 2001, 22(1): 33-37.JI Chuqun, ZHOU Weijiang. A Numerical Simulation of Aerodynamic Characters for Bell Capsule [J]. Spacecraft Recovery and Remote Sensing, 2001, 22(1): 33-37. (in Chinese)

[3]吕俊明, 程晓丽, 王强. 火星科学实验室气动特性数值分析 [J]. 力学与实践, 2013, 35(1): 31-35.LV Junm ing, CHENG Xiaoli, WANG Qiang. Numerical Aerodynam ic Analysis of Mars Science Laboratory [J]. Mechanics in Enginering, 2013, 35(1): 31-35. (in Chinese)

[4]李治宇, 杨彦广, 袁先旭. 基于 Euler方程的返回舱气动外形优化设计方法研究 [J]. 空气动力学学报, 2012, 30(5):653-657.LI Zhiyu, YANG Yanguang, YUAN Xianxu. The Study of the Reentry Capsule Shape Optimization Method Based on the Solving of the Euler Equations. [J]. Acta Aerodynam ic Sinica, 2012, 30(5): 653-657. (in Chinese)

[5]John E T, Robert D B. Multi-Objective Hypersonic Entry Aeroshell Shape Optim ization [J]. Journal of Spacecraft and Rockets, 2009, 46(5): 957-966.

[6]John E T, Robert D B. Aerothermodynam ic Shape Optimization of Hypersonic Entry Aeroshells [C]. 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Fort Worth, Texas, 13-15 September, 2010.

[7]Deb K. Multi-Objective Optimization Using Evolutionary Algorithm [M]. Chichester: John W: ley & Sons, 2002.

[8]Slawomir K, Leifur L. Transonic Airfoil Shape Optim ization Using Variable-Resolution Models and Pressure Distribution Alignment [C]. 29th AIAA Applied Aerodynam ics Conference, Honolulu, Hawaii, 2011.

[9]Li H, Lin P, Yang Z. Modeling and Design Optimization of a Common Aero Vehicle w ith Parameterized Configuration [C].AIAA Modeling and Simulation Technologies Conference, M inneapolis, M innesota, 2012.

[10]Donald R J, Matthias S, William J W. Efficient Global Optim ization of Expensive Black-Box Functions [J]. Journal of Global Optimization, 1998, 13: 455-492.

[11]Artem A D, Edquist K, Shoenenberger M. Influence of the Angle of Attack on the Aerothermodynam ic Environment of the Mars Science Laboratory [J]. AIAA paper, 2006, 2006-3889.

[12]车竞, 唐硕, 何开锋. 类乘波体飞行器气动加热的工程计算方法 [J]. 弹道学报, 2006, 18(4): 93-96.CHE Jing, TANG Shuo, HE Kaifeng. Aerothemo Engineering Method for Quasi-Waverider Vehicle [J]. Journal of Ballistics,2006, 18(4): 93-96. (in Chinese)

[13]Ricardo M P, André R D C, Curran C. Comparison of Surrogate Models in a Multidisciplinary Optimization Framework for Wing Design [J]. AIAA Journal, 2010, 48(5): 995-1006.

[14]Lophaven S N, Nielsen H B, Sondergaard J. DACE a Matlab Kriging Toolbox [R]. Technical University of Denmark, 2002.

[15]Deb K, Pratap A, Agrawal S. A Fast and Elitist Multi-objective Genetic Algorithm: NSGA-II [R]. IEEE Transactions on Evolutionary Computation, 2000, 6(2): 182-197.