EPS用永磁同步电机无位置传感器混合控制*
孙 可,陈 慧
(同济大学汽车学院,新能源汽车工程中心,上海 201804)
前言
电动助力转向系统(electric power steering,EPS)已逐渐成为现代汽车助力转向系统的主要发展方向。永磁同步电机(permanent magnet synchronous motor,PMSM)由于其功率密度高、体积小、转动惯量小、损耗转矩小和可靠性高等优点,正越来越多地应用于EPS系统中[1]。而在永磁同步电机的各种高性能转矩控制中,电机转子位置信息必不可少。为获取精确的转子位置信息,通常选用旋转变压器或霍尔编码器,但旋转变压器成本高,霍尔编码器精度低、温度适应性差,且机械式传感器的引入会使系统更加复杂,降低了系统的可靠性。因此,从降低EPS的系统成本和提高其可靠性的角度考虑,无位置传感器控制技术在EPS中具有重要的应用价值。
目前,PMSM无位置传感器控制技术可分为适用于低速和中高速的两类方法。电机处于低速时利用电机凸极性来检测转子位置,主要为高频信号注入法[2-4]:在电机中注入特定频率的高频信号,通过解调高频感应电流来获取转子位置信息。此种方法利用电机结构性凸极或饱和性凸极来获取位置信息,不受电机参数变化的影响,但随着电机转速的增大,信号处理复杂,高速区动态性能下降,估算效果变差,因此较适用于低速区。中高速时通过电机的反电动势估计转子位置信息,主要有磁链估计法[5]、状态观测器法[6-7]、模型参考自适应法[8]等。此类方法结构相对简单,动态性能好,但对电机参数敏感,在低速区由于信噪比降低,很难准确提取转子位置信息,因此较适于中高速运行。
为了实现PMSM全速域无位置传感器控制,须在低速时采用高频信号注入法,中高速区采用基于反电动势的方法,即将两类方法结合起来。通常两类方法结合的方式采用直接切换的方式[9],而为了保证两类算法之间的平滑切换,还有采用加权函数对两种算法的位置误差信号进行融合的方法[10]。本文中以EPS为应用对象,以电机转矩波动为重点指标,探讨PMSM无位置传感器的混合控制策略,在分别介绍脉动高频电压信号注入法和D状态观测器法的基础上,讨论两种方法切换的规则和切换区间,利用系数加权对两种方法估计的转速进行融合,从而保证算法的平滑切换,同时对电机输出转矩进行分析,通过仿真验证了混合控制下电机转矩波动指标满足EPS的要求。
1 脉动高频电压信号注入法
脉动高频电压信号注入法[2-4]即在转子同步旋转dq坐标系下,在d轴上注入高频正弦电压信号。在dq坐标系下,若注入的高频信号频率远大于电机运行基波频率,可得到PMSM的高频电压模型为
脉动高频电压注入法只在估计的同步旋转坐标系的d轴注入高频正弦电压信号,假设注入信号的频率为ωh,幅值为Vh,注入信号为
则可以得到高频电流为
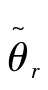
通过带通滤波器将注入信号频率下的q轴电流信号提取后,对其进行幅值调制,并经低通滤波器(LPF)后可得到用于估计转子位置的误差信号,即
利用上述转子位置误差信息,可以构造出转子位置观测器,如图1所示。
2 基于D状态观测器的方法
D状态观测器[6]是在通用旋转坐标系下,依据电机模型观测出转子磁链的大小和方向。如图2所示,正交的γ-δ坐标系即为以任意角速度ω旋转的通用坐标系,旋转方向定义从γ轴向δ轴方向为正。由于所观测出的转子磁链是在通用旋转坐标下,因此还须构建一个锁相环,将通用旋转坐标系的γ轴锁定在d轴上。
在通用旋转坐标系下,PMSM的电磁特性方程[6]为
上述式中2×1矢量V1、i1和Φ1为定子电压、电流和磁链;Φf为常数;ωγ为转子电角速度;s为微分算子;I为单位矩阵。
由式(6)~式(10)可构建如下状态观测器来估计转子磁链:

式中:g1=const,g2=const>0。
通过D状态观测器可以得到γ轴上的转子磁链,其相位估计值也为γ轴上,因此需要锁相环将γ轴锁定在转子N极上。通过位置误差信息构建一个闭环相位同步控制器,即可将转子速度同步估计出来。位置估计模块的锁相环等效模型如图3所示,其中相位比较器(PD)、压控振荡器(VCO)和低通滤波器分别为锁相环的3个基本组成部分。
3 转子位置自检测混合控制方法
为了实现永磁同步电机在全转速域内的无位置传感器控制,须将脉动高频电压信号注入法和D状态观测器法结合起来。最简单的方式是采用直接切换的方法,但考虑到保证平滑切换的原则,本文中采用在过渡阶段由两种方法进行系数加权的方式共同决定。PMSM无位置传感器混合控制的系统结构如图4所示。
混合控制算法的重点是选定合适的切换区间和设计系数加权算法。其中需要遵循两个基本原则:(1)保证在切换区间内,两类算法的估计效果相差不大;(2)保证两类算法实现平滑切换,在切换区间内,电机转矩输出性能不会有严重的恶化。为了讨论确定混合控制算法切换区间,进行了相关仿真实验。其中电机参数采用一台EPS用助力电机的参数,如表1所示。
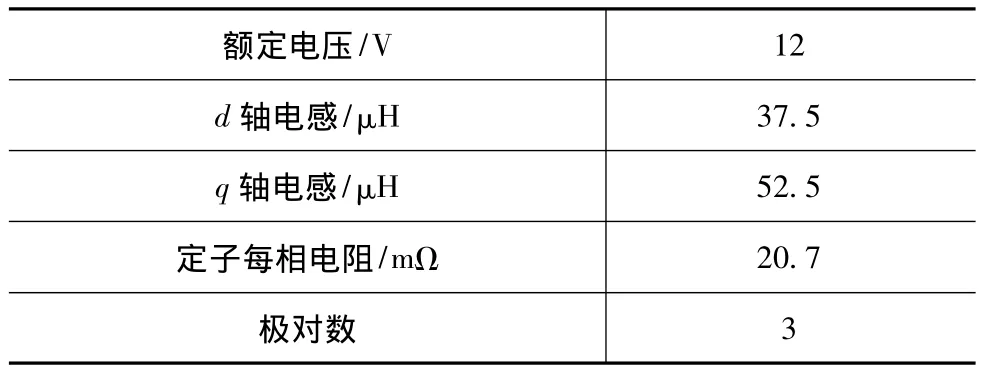
表1 永磁同步电机的参数
综合考虑EPS的指标要求,仿真实验中,选择注入高频信号的幅值为1V,注入频率为1kHz。令输出转矩的目标指令值为恒值,通过缓慢增加电机的转速,来分别观测两类算法在不同转速下的转子位置估计效果,从而选定算法切换区间。图5和图6分别为高频信号注入法和D状态观测器法在电机转速为10~15rad/s时的转子位置估计结果。
由图可见,永磁同步电机转速在5s内由10增加到15rad/s,两种算法的转子位置估计误差在±1°电角度,估计误差基本相当,且该转速区间内两种算法位置误差基本保持不变,满足切换区间内两种算法估计效果不会出现突变的要求。因此,选择转速10~15rad/s为两种算法的切换融合区间。在切换区间内,对两种算法采用系数加权的方法以实现平滑过渡,加权算法如图7所示。此外,为减小注入的高频信号对电机输出性能的影响,当过渡到中高速后,在15~20rad/s的区间内匀速将高频注入电压信号的幅值减小直至为零,相当于在中高速下仅有D状态观测器工作。而当电机转速低于20rad/s时,高频电压信号又会重新注入到电机内。
4 无位置传感器混合控制系统仿真实验
在Simulink中搭建了PMSM无位置传感器混合控制系统仿真模型,采用永磁同步电机矢量控制中id=0的控制方法,对混合控制系统的估计效果和电机转矩波动指标进行仿真验证。仿真实验中,电机输出转矩指令值设为恒定值1.44N·m,电机转速指令值和仿真实验结果如图8所示。
图8中电机转速指令值从0开始,匀速增加到25rad/s,保持恒速4s后,由25rad/s减到0,并保持零速4s。由仿真结果可以看出,算法切换第1次发生在5.6~6.4s,第2次发生在13.6~14.4s。混合控制下,电机转速估计值可以很好地跟踪目标值;高频信号注入法加权系数Kh的变化符合设计的加权函数;电机转子位置估计值也可以很好地跟踪实际值,最大位置估计误差在±2°电角度。估计系统在算法切换区间可以完成平滑过渡。
图9为混合控制下电机转矩输出仿真结果。可以看出,在0s时刻,即使电机转速为零,电机转矩输出也可以很好地跟踪指令值。高频信号注入法工作阶段,1kHz高频信号对输出转矩波动产生了影响,相比之下中高速时的转矩波动则明显小很多。而由图中还可以看出,当算法切换结束后,由于高频注入信号的幅值逐渐趋于零,中高速下实际仅有D状态观测器工作。对输出转矩进行分析发现:高频信号注入法单独工作且维持在零速时,最大转矩波动约为2.1%;加减速时,高频信号注入法最大转矩波动约为2.8%;D状态观测器法单独工作,最大转矩波动约为1%;切换区间内最大转矩波动约为3%。因此,混合控制下的电机转矩波动表现满足EPS转矩波动指标在2% ~5%的技术要求[11]。
为进一步分析电机输出转矩波动的频率成分,仿真实验中将转矩指令值设定为幅值1.44N·m,频率为5Hz的正弦信号。对电机转矩输出结果进行频谱分析,如图10所示。由图中可以看出,输出转矩波动中存在1kHz附近的高频波动成分,这正是由注入的高频信号引起的。考虑到EPS中机械时间常数远大于电气时间常数,频率高于50Hz的转矩波动会被机械系统滤除,不会反映到转向盘上。因此,上述高频信号注入法中3%左右的最大转矩波动,在EPS上会被机械系统滤除高频成分,电机输出转矩波动对EPS的影响会进一步降低。因此,在理论上永磁同步电机无位置传感器混合控制策略应用于EPS是可行的。
5 结论
探讨了基于脉动高频信号注入法和D状态观测器法的EPS用永磁同步电机无位置传感器混合控制方法。低速时采用对电机参数不敏感的脉动高频电压注入法,中高速时采用算法更加简单的D状态观测器法。通过仿真分析选取了混合控制的算法切换区间,并在切换区间内对两种算法进行系数加权。仿真结果表明,以EPS作为应用对象,脉动高频电压信号注入法和D状态观测器法电机输出转矩波动均低于3%,满足转矩波动的技术要求,并且在算法切换的混合控制区间,估计系统可以做到平滑过渡,EPS用永磁同步电机无位置传感器混合控制方法理论上具有可行性。
[1] 陈慧,杨磊,南楠,等.汽车转向系统电子化技术发展[M].北京:北京理工大学出版社,2008:35-69.
[2] 秦峰,贺益康,刘毅,等.两种高频信号注入法的无传感器运行研究[J].中国电机工程学报,2005,25(5):116 -121.
[3] Ji-Hoon J,Seung-Ki S,Jung-Ik H,et al.Sensorless Drive of Surface-mounted Permanent-magnet Motor by High-frequency Signal Injection Based on Magnetic Saliency[J].IEEE Transactions on Industry Applications,2003,39(4):1031 -1039.
[4] 冯英本,陈慧.基于高频信号注入的EPS用SPMSM无传感器控制[J].吉林大学学报(工学版),2011(S2):65-69.
[5] Batzel T D.Improved Angular Velocity Estimation for High Performance Sensorless PMSM[C].Power Electronics in Transportation,2004:89 -96.
[6] Shinnaka S.New“D-State-Observer”-Based Vector Control for Sensorless Drive of Permanent-magnet Synchronous Motors[J].IEEE Transactions on Industry Applications,2005,41(3):825 -833.
[7] 陈福海,陈慧,冯英本.EPS用永磁同步电机准无位置传感器控制[J].汽车工程,2010,32(7):617 -620.
[8] 王庆龙,张崇巍,张兴.基于变结构模型参考自适应系统的永磁同步电机转速辨识[J].中国电机工程学报,2008,28(9):71-75.
[9] Andreescu G,Pitic C I,Blaabjerg F,et al.Combined Flux Observer with Signal Injection Enhancement for Wide Speed Range Sensorless Direct Torque Control of IPMSM Drives[J].IEEE Transactions on Energy Conversion,2008,23(2):393 -402.
[10] 王高林,张国强,贵献国,等.永磁同步电机无位置传感器混合控制策略[J].中国电机工程学报,2012,32(24):103 -109.
[11] Guang L,Kurnia A,De Larminat R,et al.Position Sensor Error Analysis for EPS Motor Drive[C].Electric Machines and Drives Conference,2003:249 -254.

