GPU编程模型中存储体冲突的研究

2013-10-09 03:28原建伟李爱国李文宇

河北工业科技 2013年1期

原建伟，李爱国，李文宇

（陕西工业职业技术学院信息工程学院，陕西咸阳 712000）

随着计算机技术的不断发展，新技术层出不穷，不断提高应用水平，近年来随着GPU技术的不断发展，其强大的浮点运算能力及并行运算处理能力协助CPU运算，甚至在某些领域成为了CPU有力的竞争对手［1］。GPU强大的并行计算能力被充分运用在很多领域，在信息处理领域里，文献［2］中使用GPU实现了数据挖掘算法，文献［3］在GPU上加速了DCT快速变换。越来越多的算法和应用在GPU上实现，编程模型也越来越成熟，但在基于GPU的编程模型中，影响并行效率的因素也很多，处理不好，不仅不能充分发挥GPU的并行能力，甚至会降低运算速度。这些因素中存储体冲突（bank conflict）执行效率的影响较大，本文针对存储体冲突进行研究与探讨，并提出解决方法。

1 存储体冲突分析

在GPU结构中，Bank是指共享内存按照固定大小（通常为4Byte）划分为若干存储模块。GPU进行并行运算过程中，线程对Bank的访问通常以half-warp为组同时进行，无需以对齐的方式访问，但要求线程与Bank一一对应。如果同时有多个线程对同一个Bank进行操作，就产生了访问冲突，访问时间将根据冲突的线程数量成倍增加。

由于共享存储器位于芯片上，因而共享存储器空间比本地和全局存储器空间的速度都要快得多。实际上，对于Warp块中的所有线程来说，只要线程间不存在存储体冲突，访问共享存储器的速度与访问寄存器一样快。为了获得较高的存储器带宽，共享存储器被划分为多个大小相等的存储器模块（Bank），这些存储体可同步访问。因此，对落入n个不同存储体的n个地址的任何存储器读取或写入请求都可同步实现，得到更有效的带宽，可达到单独一个模块的带宽的n倍，但若一个存储器请求的2个地址落入同一个存储体内，就会出现存储体冲突［4］。

共享内存冲突产生的根本原因来源于计算机本身的设计问题。引起存储体冲突的诱因是并发存储器访问。内存在工作的时候一次只能设置一个存取地址，因此其存取形式为串行，而GPU是多核结构，其核心数量较多执行线程数量更多，为了与GPU的众多线程匹配，需要更大带宽的共享内存来提高效率。对于这样的需求，可以通过多端口存储器来加速访问速度，但是对于作为共享内存的Cache或者DRAM都只有一个端口，原因是制造多端口存储器的成本非常高，为了实现这样的模型，实际上采用将多个相同的单独存储器合并成内存组即一个Bank，这样就形成了相当于多端口的存储，但在一个Bank内依然采用顺序存储。

在CUDA的编程模型中，多处理器SIMT单元以32个并行线程为一组来创建、管理、调度和执行线程，这样的线程组称为 Warp块［4］。一个 Warp块要去同时读写不同地址上的数据时，硬件不允许每个地址都设置一个存取端口，只能在一个跨距（以16个4Byte为单位）内为每个地址设置不同的端口，即每一个地址都有自己独立的读写端口，这就导致每过16个4Byte的跨距就会产生一次与当前地址发生读写冲突，访问时间将根据冲突的线程数量成倍增加。

基于CUDA模型的GPU会在必要的时候自行解决冲突，采取的方法是将存在存储体冲突的存储器请求分割为多个不冲突的请求，此时有效带宽将降低为原带宽除以分离后的存储器请求的数量。

2 解决存储体冲突的方法

2.1 一般性原则

在CUDA中，为了尽可能提高计算性能，应该尽量最小化存储体冲突。可以通过以下方式在程序设计过程中做相应处理以减少存储体冲突的产生。根据存储体的组织方式，将Warp块的共享存储器请求分割为上下两部分，属于Warp块第1部分的线程和属于Warp块第2部分的线程之间不可能出现存储体冲突。

一种常见的情况是各线程访问数组中的32位字，使用线程ID tid进行索引，步幅为s：

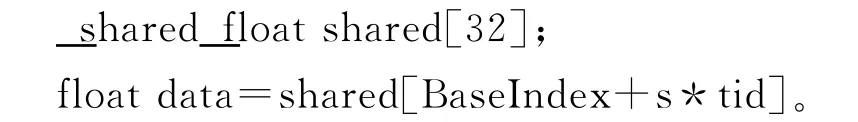
只要s＊n是存储体m数量的倍数，或者说只要n是m／d的倍数（其中d是m和s的最大公约数），线程tid和（tid＋n）访问的就是同一个存储体。因而，只有在 Warp块的一半大小小于等于m／d时，才不会存在存储体冲突。对于计算能力是1.x的设备，可以说只有在d等于1时，或者说只有在s是奇数时，才不会存在存储体冲突［4］。

另一种情况就是，当一个half-warp的所有16个线程同时访问同一个Bank的32bit数据时，该Bank以广播的方式将数据发送给所有线程，因此不会产生访问冲突。

矩阵运算由于其计算量巨大、耗时长，往往通过并行算法提高执行效率。同样在基于图形处理器的并行运算环境中矩阵的运算也常常出现。通常情况下，矩阵元素可以存储在Bank里，第i个数据存储在第16个Bank中，即划分子矩阵时每个Block处理矩阵的宽度为16的整数倍。如果线程访问Bank是对齐的就不会有冲突。

在CUDA中一个Block中线程数量的最大值为512，如果矩阵规模小于512时，矩阵按行划分，并将块对应的数据映射到处理单元上，当矩阵规模大于512时，可以将矩阵分成二维块，每个块的大小为16×16，二维块的线程数为256，为了减少计算过程中对全局存储器的访问，将计算过程中经常使用的x（k），x（k＋1）存储在共享存储器内［5］。

由于不同数据类型的数据占用存储单元的差别，设计不合理时也会带来存储体冲突。当使用Char型数据时，由于其每个数据长度是8bit，因此每个Bank中就包含了4个数据。线程在顺序访问内存时就会出现4个线程访问同一个Bank的情况，即产生了4路访问冲突［5］。对于结构体赋值将在必要时编译为针对结构体中各成员的多个存储器请求，因此结构体内部成员的这种并行存储请求也会导致存储体冲突。

2.2 实例分析

根据对本院学生访问在线学习系统的情况进行数据挖掘，采用K均值（K-means）算法研究用户访问行为，K均值算法是一种基于划分的聚类算法，因为它有理论上可靠、算法简单、速度快等优点而被广泛使用［6-9］。

聚类算法处理的数据量都很大，且大量的计算都是在同一数据结构上的不同部分进行操作，数据在处理期间是分布式存放，因此很适合采用数据并行方法编程。

K均值算法在处理大数据集时相对可伸缩且效率高，该算法的复杂度是O（nkt），其中n是所有对象的数目，k是簇的数目，t是迭代的次数。通常情况下k≪n，且t≪n。当n非常大的时候，K均值算法时间主要耗费在距离计算过程中，且距离计算完全可以分成相同的块同时进行计算，可以根据GPU中流处理器的数量将n个数据分成一定的份数分别进行计算，然后根据每一个流处理器计算出各自子数据集中数据与k个类的中心距离从而得到局部聚类结果，然后再汇总得到全局聚类结果［3］。

这里采用平方误差准则，其定义为下式：

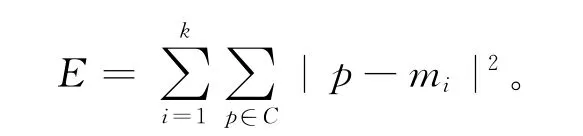
式中：E是数据中所有对象的平方误差的总和；p是空间中的点，表示给定的数据对象；m是簇Ci的平均值［10］。

算法实现如下：

1）先将数据分成若干块存入共享内存；

2）选择任意k个对象作为初始聚类中心；

3）分别在GPU的运算单元中，根据每个聚类中所有对象的均值（中心对象）计算样本集中每个对象与这些中心对象的欧几里德距离；

4）将各个计算单元中的数据进行汇总，并根据最小距离重新对相应对象进行划分；

5）更新聚类均值，即计算每个（有变化）聚类的均值（中心对象）；

6）重复步骤3）到步骤5）直到每个聚类不再发生变化为止。

很多K均值算法中的数据结构都是采用数组来存储分类元素，但聚类算法的特殊性决定了每一次计算之前都不能确定每一分类的元素数目，为了避免这个问题，往往采用比较大的数组进行存储，但是GPU的存储容量有限，为了提高效率，可以采用结构体并设置一个域来区分元素属于哪一个分类。但由于结构体成员定义的差异会出现不同的存储体冲突。

如果结构体内部成员使用奇数个32位字作为步幅访问存储器就不会出现存储体冲突，相反采用偶数个32位字作为步幅访问存储器就会产生存储体冲突，不同类型冲突情况见表1。

表1 不同类型冲突情况Tab.1 Bank conflict because of different type of data

本例中使用以下的数据结构实现分类元素的存储，用于避免存储体冲突的发生。

struct ClassicData｛

unsigned int num；／／定义数据大小

data＊attributes；

unsigned int＊belongTo；／／确定数据属于哪一个聚类

｝

本文的实验平台为NVIDIA 8800GT GPU，内建24个流处理器，INTEL E8400 3.0GHz CPU，数据来源为校园网中学生对在线学习系统访问情况的相关日志，根据学生访问该系统不同内容页面，分析学生在线学习的行为特征。原始数据在经过数据清洗、用户识别等步骤之后，得到5 327个用户对《计算机应用基础》课程在线教学网站的访问数据（访问时间，阅读时长等）。对上述数据进行聚类分析研究学生对该网站不同内容的页面访问的行为特征。表2显示了有存储体冲突与没有存储体冲突的两种情况下不同用户量访问数据进行聚类分析的用时，有冲突情况下计算时间约是无冲突情况下的56～190倍，并且随着数据量的增大，存储冲突带来的低效率也就越明显，有无冲突计算时间曲线见图1。

表2 有无冲突的计算时间对比Tab.2 Comparison of computing time with or without Bank conflict

图1 有无冲突计算时间曲线Fig.1 Computing time curve with or without Bank conflict

3 结语

通过研究可见，CUDA编程模型中存储体冲突的根本原因在于目前计算机体系中并发存储器访问的机制，因此在不能改变硬件的情况下，通过算法改良解决存储体冲突是行之有效的方法，通过多种手段对算法进行优化，可防止存储体冲突的产生，进一步提高GPU并行运算的效率。

／References：

［1］KENNETH M，EDWARD A.The FFT on a GPU［A］.Proceedings of the ACM Siggraph／Eurographics Conference on Graphics Hardware［C］.San Diego：［s.n.］，2003.112-119.

［2］刘琳，何剑锋，王红玲.GPU加速数据挖掘算法的研究［J］.郑州大学学报（理学版），2010，42（2）：31-34.LIU Lin，HE Jianfeng，WANG Hongling.Study of the data mining algorithm with GPU acceleration［J］.Journal of Zhengzhou University（Natural Science Edition），2010，42 （2）：31-34.

［3］阮军，韩定定.基于CUDA的DCT快速变换实现方法［J］.微电子学与计算机，2009，26（8）：201-205.RUAN Jun，HAN Dingding.An efficient implementation of fast DCT using CUDA［J］.Microelectronics &Computer，2009，26（8）：201-205.

［4］NVIDIA.Corporation CUDA2.0编程指南［EB／OL］.http：／／down.csdn.net／detail／gaopengpian／2788197，2010-10-27.NVIDIA.Corporation CUDA2.0programming guide［EB／OL］.http：／／down.csdn.net／ detail／gaopengpian／2788197，2010-10-27.

［5］姚远，王涛，张丹，等.基于通用图形处理器的Jacobi算法研究［J］.信息工程大学学报，2010，11（3）：336-338.YAO Yuan，WANG Tao，ZHANG Dan，et al.Research on Jacobi algorithm based on general purpose graphical processing unit［J］.Journal of Information Engineering University，2010，11（3）：336-338.

［6］孟海东，李秉秋.聚类分析在县域经济发展研究中的应用［J］.河北工业科技，2012，29（2）：116-119.MENG Haidong，LI Bingqiu.Application of cluster analysis in regional economy research［J］.Hebei Journal of Industrial Science and Technology，2012，29（2）：116-119.

［7］李冬梅，陈军霞.聚类分析法在公交网络评价中的应用［J］.河北科技大学学报，2012，33（3）：279-282.LI Dongmei，CHEN Junxia.Application of cluster analysis in evaluation of public traffic network［J］.Journal of Hebei University of Science and Technology，2012，33（3）：279-282.

［8］张娟，高克峰，张曦.从文本中学习本体的系统设计［J］.河北工业科技，2011，28（3）：160-163.ZHANG Juan，GAO Kefeng，ZHANG Xi.Design of system of learning ontology from texts［J］.Hebei Journal of Industrial Science and Technology，2011，28（3）：160-163.

［9］叶若芬，孙书明.基于数据挖掘技术的教学测评［J］.河北工业科技，2011，28（6）：383-385.YE Ruofen，SUN Shuming.Teaching evaluation based on data mining technology［J］.Hebei Journal of Industrial Science and Technology，2011，28（6）：383-385.